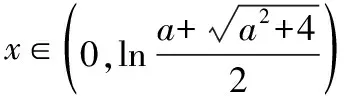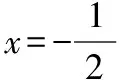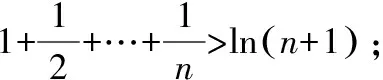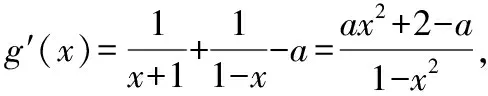含参数不等式恒成立问题的破解方法

安徽

张 威 刘昌敏

(作者单位：安徽省蚌埠市五河县高级中学)

含参数不等式恒成立问题的破解方法

安徽

张 威 刘昌敏

在高考题中，每年都要设计一道函数大题，其中有一类是研究不等式在一个区间上成立时某个参数的取值范围问题，这类问题利用常见的基本初等函数的知识已经无能为力，此时就需要根据导数的方法进行解决．使用导数的方法研究不等式恒成立的基本思路是构造函数，通过导数的方法研究这个函数的单调性、极值和最值，利用这些函数性质推断不等式成立的情况．因为导数的引入，为函数问题的解决提供了操作工具.因此入手时大家比较清楚，但是深入解决函数与不等式相结合的题目时，往往一筹莫展.原因是找不到两者的结合点，不清楚解决技巧.本文将呈现出针对解答题恒成立问题的几种类型和破解方法.

【方法一】分离参数，构造新函数，求其最大值或最小值

此方法的具体解题步骤是：①分离参数；②构造新函数，求其导数；③判断新函数的单调性(一般通过一次求导或二次求导进行判断)；④利用其单调性求出该函数所需要的最值；⑤根据不等关系，求出参数范围.

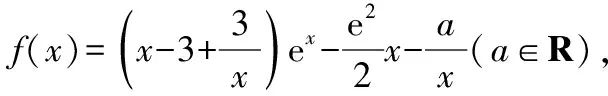
(直接分离参数)

(构造新函数)

g′(x)=x[(x-1)ex-e2]，

(求导判断单调性)

令h(x)=(x-1)ex-e2,h′(x)=xex≥0，

(再次构造新函数，进行二次求导)

所以h(x)=(x-1)ex-e2在[0,+∞)上单调递增，

且当x∈(0,2)时，h(x)<0，即g′(x)<0，

当x∈(2，+∞)时，h(x)>0，即g′(x)>0，

所以g(x)在(0,2)上单调递减，在(2,+∞)上单调递增，

所以g(x)≥g(2)=-e2，所以a≤-e2.

(根据单调性求其最小值，得到参数范围)

【点评】此题思路明确，难度不大，关键点和难点是：①如何求出所构造的新函数的单调性；②一次求导后如何再次构造出新函数(有时并不是一次求导后的函数，可能选取的只是其部分解析式).

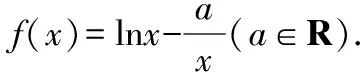
(Ⅰ)当a<0时，求函数f(x)的单调区间；

(Ⅱ)若函数f(x)在x∈[1,e]上的最小值为4，求a的值.

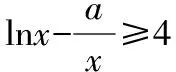
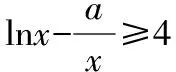
通过上述例题和变式，可以发现利用分离参数求解含参恒成立问题，避免了对参数的讨论，使问题变得更明朗，但有时也会遇到分参后，构造的新函数在端点处函数无意义，此时即使得到新函数的单调性，也无法求出最值，那么有的学生会利用大学的知识洛必达法则求其在端点处极限值，但是洛必达法则在高考中属于超纲知识，还是要慎用，那么还有什么样的方法可以解决这类问题呢？请继续看下面的方法.

【方法二】分离函数，切线搭桥，柳暗花明

此方法的具体解题步骤是：①分离函数；②求切线方程；③证明两个函数的不等关系；④得到满足充分条件的参数范围；⑤再证明出必要条件的参数范围不满足条件.

【例2】(2006·全国卷Ⅱ理·20)设函数f(x)=(x+1)·ln(x+1).若对所有的x≥0，都有f(x)≥ax成立，求实数a的取值范围.

【解析】为了减少计算，进行如下换元：令t=x+1≥1，

所以原命题“对∀x∈[0,+∞)，都有f(x)≥ax成立”

等价于“对∀t∈[1,+∞)，恒有tlnt≥a(t-1)成立”.

(分离函数)

令g(x)=xlnx(x≥1)，则g′(x)=1+lnx，所以g(x)在[1,+∞)上单调递增，

因为g′(1)=1,g(1)=0，所以g(x)在点(1,0)处的切线方程为y=x-1，

(求切线方程)

令h(x)=xlnx-x+1，则h′(x)=lnx，所以h(x)在[1,+∞)上单调递增，

所以h(x)≥h(1)=0，所以xlnx≥x-1，当且仅当x=1时，取等号，

所以tlnt≥t-1，当且仅当t=1时，取等号，

(证明不等关系)

所以若对∀t∈[1,+∞)，恒有tlnt≥a(t-1)成立，则a≤1一定满足，

又当a>1时，令F(t)=tlnt-a(t-1),F′(t)=1+lnt-a，

(判断必要性)

可得F(t)在(1,ea-1)上单调递减，所以当t∈(1,ea-1)时，tlnt

综上，a≤1.

【点评】此题如果利用方法一强行分参，求到最后可以发现，构造的新函数在端点处无意义.利用此方法很好的避免了对参数的讨论，同时也规避了在端点处无意义的情况.利用此法的关键是利用切线方程搭桥得到满足充分条件的参数范围，再构造新函数判断必要条件的参数范围不满足条件.有的学生认为借助函数的图象，不是显然成立吗？还有必要进行必要性的判断吗？在高考的解答题中，数形结合思想解题是不严谨的解法，故请读者慎用数形结合思想解主观题.

【变式训练】(2007·全国卷Ⅰ理·20)设函数f(x)=ex-e-x.

(Ⅰ)证明：f(x)的导数f′(x)≥2 ；

(Ⅱ)若对所有x≥0都有f(x)≥ax成立，求a的取值范围.

【解析】(Ⅰ)略.(Ⅱ)由题知，f′(x)=ex+e-x，所以f′(0)=2，

所以f(x)在点(0,0)处的切线方程为y=2x，

令g(x)=ex-e-x-2x，g′(x)=ex+e-x-2，由(Ⅰ)可知g′(x)≥0恒成立，

所以g(x)在[0,+∞)上单调递增，即ex-e-x≥2x，当且仅当x=0时，取等号，

所以当对所有x≥0，都有f(x)≥ax成立时，可得a≤2满足条件，

又当a>2时，令h(x)=ex-e-x-ax,h′(x)=ex+e-x-a，

综上,a≤2.

【点评】此题和例2解法一样，解题的关键点还是要把握解法的充要性，有的学生可能只进行充分性解题，没有进行必要性的判断，那么这个解法是不完整的，在考试中，只能得一半分.

上述方法如果运用到客观题中，再结合数形结合思想，那么就没有必要进行必要性判断，但是主观题中，还是必须进行必要性判断，保证解法的严谨性.下面请读者继续品读破解恒成立问题的其他解法.

【方法三】利用有效的“探路”点，得到满足条件的必要条件，减少对参数的讨论次数

高考中有的恒成立(任意性)问题进行直接分参求解时，往往计算量很大，可能有的题目利用高中的知识无法解决，所以只能对其直接构造，对参数进行分类讨论，我们知道对参数进行分类讨论是一个烦琐和易错的过程，如何减少对参数的讨论次数就显得至关重要.此方法就是利用特殊点函数值，减少对参数的讨论的次数.具体解题步骤是：①直接构造新函数；②利用有效的“探路”点，求出参数的一个必要条件；③在②中求出的必要条件下对参数进行讨论，求其单调性、最值；④下结论.

【例3】(2017·全国卷Ⅱ文·21)设函数f(x)=(1-x2)ex.

(Ⅰ)讨论函数f(x)的单调性；

(Ⅱ)当x≥0时，f(x)≤ax+1，求a的取值范围.

【解析】(Ⅰ)略.(Ⅱ)由已知可知，当x≥0时，ax+1+(x2-1)ex≥0恒成立，

令g(x)=ax+1+(x2-1)ex，由题意可得g(1)≥0恒成立，即a≥-1，所以满足条件a的集合是{a|a≥-1}的子集，故只需讨论a≥-1的情况即可.

(利用端点值，把参数范围缩小，减少讨论情况)

则g′(x)=a+(x2+2x-1)ex，设h(x)=a+(x2+2x-1)ex，

则h′(x)=(x2+4x+1)ex>0，所以g′(x)在[0,+∞)上单调递增，

又g′(x)min=g′(0)=a-1，当a≥1时，g′(x)≥0，所以g(x)在[0,+∞)上单调递增，所以g(x)≥g(0)=0，此时满足条件；

当-1≤a<1时，g′(0)<0,g′(1)=2e+a>0,

(此时发现缩小a的范围的好处)

所以g′(0)·g′(1)<0,且g′(x)在[0,+∞)上单调递增，所以存在唯一x0∈(0,1)，

使得g′(x0)=0，所以g(x)在[0,x0]上单调递减，在[x0,+∞)上单调递增，

所以当x∈[0,x0]时，g(x)≤g(0)=0，此时不满足条件.

综上所述,a≥1.

【点评】此类型题目，思路很明确，就是构造函数，分类讨论求单调性、最值.但是如果不利用特殊点进行有效的“探路”，那么就复杂多了，在高考这个争分夺秒的时刻，能使得计算简便、减少解题时间是多么的难能可贵.对于这个有效的“探路”点的选取有时选择区间端点，有时是其他点，无论是哪个点，只要能达到减少对参数讨论的次数，那么它都是有效的“探路”点.

(Ⅰ)求a的值及f(x)的最大值；

(Ⅲ)设g(x)=b(ex-x)，若g(x)≥f(x)恒成立，求实数b的取值范围.

【解析】(Ⅰ)略.(Ⅱ)略.

(Ⅲ)“不等式g(x)≥f(x)恒成立”等价于“当x>-1时,F(x)=g(x)-f(x)≥0恒成立”，

由题意可得,F(0)≥0，即b≥0，

即满足条件的b的集合是{b|b≥0}的子集，接下来只需要考虑b≥0的情况即可.

对b≥0进行分类讨论，即可求出b≥0.

【点评】此题选取的有效的“探路”点并不是区间端点值，而是x=0，极大地简化了计算.

方法三的思想给了我们很大的启发，任何题目的解法并不是一成不变，但是大致的解题方向一定有通法可循，关键在通法的基础上要形成自己的解题意识，要形成方法的迁移，只有这样，在高考中才能立于不败之地.

【方法四】直接构造函数，对参数分类讨论，巧借端点值，得到参数范围

对于方法三我们可以利用有效的“探路”点，减少对参数的讨论次数，但是有的题目选取的点不能达到其有效性，或者很难找到有效的“探路”点，此时只能对参数进行全部讨论，具体的步骤和方法三一样.

(Ⅰ)设a>0，讨论y=f(x)的单调性；

(Ⅱ)若对任意x∈(0,1)恒有f(x)>1，求a的取值范围.

【解析】(Ⅰ)略.

(Ⅱ)直接对函数f(x)进行求导有点麻烦，故对其两边取对数，再构造函数进行求解.

令g(x)=ln(x+1)-ln(1-x)-ax，

①当0≤a≤2时，ax2+2-a>0，所以g(x)在(0,1)上单调递增，

即g(x)>g(0)=0，此时满足条件；

综上所述,a≤2.

【点评】1.此题通过解析，可以发现在x∈(0,1)内很难找到有效的“探路”点，使得参数a≤2，即使找到一点使得a≤t(t>2)，通过解析可以发现x∈(2,t)这一区间依然需要进行讨论，达不到减少对参数的讨论次数；2.通过对端点值代入，可以得到g(0)=0，此时只要g(x)在(0,1)上单调递增，就一定满足条件.而如果在(0,1)范围内先减后增或单调递减，此时都不满足条件.若在(0,1)范围内，先单调递增，再单调递减，只要在单调递减的区间内找到至少一个x，使得g(x)<0，也是不满足的.

【变式训练】(2010·全国新课标卷理·21)设函数f(x)=ex-1-x-ax2(a∈R).

(Ⅰ)若a=0，求f(x)的单调区间；

(Ⅱ)若当x≥0时,f(x)≥0，求a的取值范围.

【点评】此题和例4的特点一样，只是在求解过程中，需要利用ex≥1+x这个结论进行放缩.

(作者单位：安徽省蚌埠市五河县高级中学)