新高考模式下高中数学教学方法探究

（江西省宜春市第四中学 江西宜春 336000）

一、重视基础教学

基础知识是每门学科的起点也是基石，没有扎实的基础怎么能建成高楼大厦呢？夯实基础知识是提高学生解题能力、应试能力的关键，不论是过去的高考模式还是新高考模式，基础知识都是考查的重点，细小的知识点通过问题的纽带相互交织在一起，形成一张张大网，要想解开，就必须用基础知识的利剑去各个击破。

基础知识也经常在高考试题中被单独作为考题：如集合，复数，数列及统计等内容常常单独成题。

如：（2017年全国卷（2））。为评估一种农作物的种植效果，选了n块地作试验田。这n块地的亩产量（单位：kg）分别为x1，x2，…，xn，下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是（ ）

A．x1，x2，…，xn的平均数

B．x1，x2，…，xn的标准差

C．x1，x2，…，xn的最大值

D．x1，x2，…，xn的中位数

这是一道单纯的统计类题型，知道概念就可以正确解答。

每年的高考题中，基础题所占分值还是比较可观的。要想打好基础，首先，需要重视高中数学教材中出现的各种概念、定理、公理及公式，帮助学生理解清楚，就概念来讲，教师需要引导学生注意概念中核心内容和附加条件，就定理来讲，学生需要明确定理的适用范围，切不可乱用定理，就公式来讲，学生不仅需要明确公式的使用范围，还要清楚理解公式中各变量的内涵。其次，教师需要重视对课本例题的讲解，有条理的指出具体知识点在题目中的运用方法。然后要求学生自主完成课本后练习题，并对题目进行详细讲解，这些题目同课程内容联系紧密，适当的联系能够提高学生运用知识点解决问题的熟练度，对知识点有更加深刻地认识。只要循序浙近，基础定会很牢固。

二、培养数学思维

数学思维也就是用人们通常所指的数学思维能力，即能够用数学的观点去思考问题和解决问题的能力。数学思维主要表现在思维的敏捷性，深刻性，独创性，概括性，灵活性和批判性。老师可以在数学教学中加以引导，帮助学生从以上几个方面进行训练，培养学生对问题的反应速度，对问题的分析深度，培养创新意识和独创的方法，还要学会去总结，对不同的问题要灵活对待，当然也在要有反思的态度。

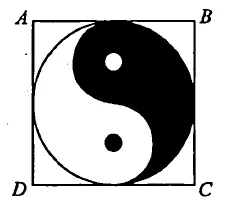
如：（2017年全国卷（4））。如图，正方形ABCD内的图形来自中国古代的太极图。正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称。在正方形内随机取一点，则此点取自黑色部分的概率是（ ）

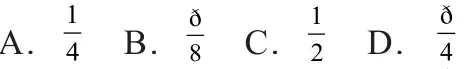
对于此题，学生只要通过认真观察就可以发现圆内的黑色部分面积与白色部分面积相等，那么黑色部分面积就是圆的面积的一半即可正确解答。

通过对数学思维的培养，在遇到问题时，就会擅长概括提炼问题，从多方面开辟思维点，从已知因素中发现新的线索，能够根据条件的变化改变思考的方向，探究问题与现实之间的联系，摆脱僵化模式，激发创造性火花，并在问题得到解决后会检验问题是否真正得到解决，发现推理过程中存在的矛盾，运算错误等问题。数学是一门严谨的学科，从知识点的构建到试题的解答，无不体现了数学学科的严谨性。因此，数学思维的培养也就特别重要。

三、提高解题能力

要想在考试中取得好成绩，不仅要有扎实的基础知识作为铺垫，而且还有要缜密的数学思维能力，还要掌握一些解题技巧。在解题时，正确地使用解题技巧能够让学生节约更多的时间并获得更高的得分率。老师在授课时可以从以下几方面传授。第一、提高审题的能力，找到问题中的已知量和未知的量；找出等量关系式或函数关系；看清关键词，力求快和准。第二、提升解题的能力，解题时充分运用方程及函数的思维方式解答，掌握必要的解题理论，熟悉基本的解题方法，模仿，运用并掌握它。再次，需要传授学生解题步骤。在高考数学测试中，解题步骤对作答的正确性有十分重要的影响。

以线性规划题的解法为例，如：（2017年全国卷（7））．

A．0 B．1 C．2 D．3

要求目标函数的最优解，需要进行画可行域，画目标函数，求最优解的解题步骤，只要计算没有问题就能快速解答。

在考试过程中，尽管有些时候学生并不一定能够完全正确的解得最终结果，但是一个合理的答题过程能够为他们正确更多得分点。

总的来讲，在新高考模式下，高中数学的有效开展依然离不开基础知识的教学、数学思维方式的培养以及解题技巧的训练。此外，为了使学生在考试过程中发挥正常水平，教师还需要强化他们的应试心理素质和抗压能力，使他们提前适应高考数学考试的紧张氛围，争取以更好的状态、更加饱满的热情迎战高考。