数形结合思想在高中数学教学中的应用

（盘锦市辽东湾实验高级中学（辽宁省实验中学辽东湾分校） 辽宁盘锦 124000）

一、数形结合在中学教学中的应用

1．利用数形结合思想解决函数最值问题

函数的最值问题，一般情况是求某个代数式或者函数的最大值或者最小值。有些是利用函数的性质解决，有些是利用不等式（均值不等式等）知识解决。针对比较复杂繁多的式子，通常采用结合其几何意义来进行分析和解决。以下是利用数形结合思想来解决函数最值问题的几个例子：[1]

（1）转化为两点间距离问题：

解析：观察式子结构，从纯代数的角度出发，很难求解，这时就应该考虑其几何意义，利用数形结合思想将代数问题转化为集合问题，巧用两地那间距离公式，即转化为：

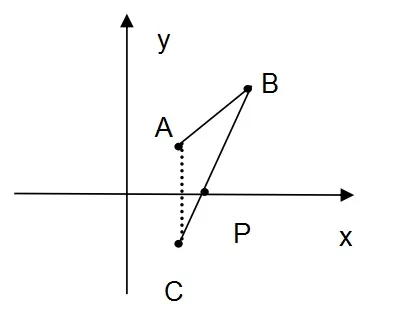
令A（1，1），B（2，2），P（x，0），则问题转化为在X轴上求一点P，使有最小值，由于AB在x轴同侧，故取A关于x轴的对称点C（1，-1），故最小值为点评：类似这种形式的函数求其最值，常采用这种找出对称点，并利用两点之间线段最短的形式来解。

（2）转化为点到直线间距离问题：

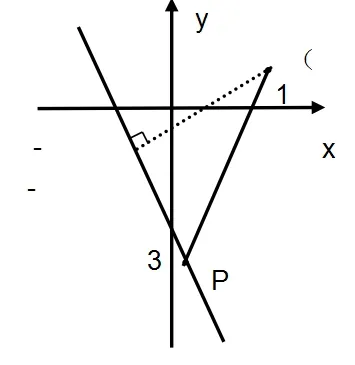
（3）转为直线斜率问题：

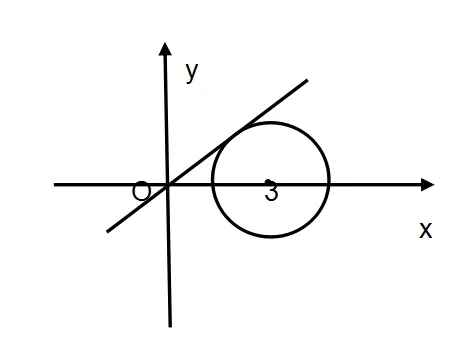
由图可见，当点A在第一象限，且与圆相切时，0A的斜率最大，经简单计算，得最大值为：

总之，“数”和“形”的结合是依靠题目特征，即所包含的几何意义而存在的。在做题的时候，首先要确定此题目是否具备应用数形结合思想的特征，如果通过对题目的观察、分析之后确定了思想，那么其次就要考虑题目中的哪些数量关系可以转化成其几何意义，找准了几何意义之后就可以借助图形来解决问题了。[2]

2．利用数形结合思想解决线性规划问题

相性规划问题是完全应用图形进行解答的一种类型题目，每套高考题都会有填空题或者选择题，已经成为了高考的热点题 ，如果学生可以准确把握题目本质，即可解答。

案例：

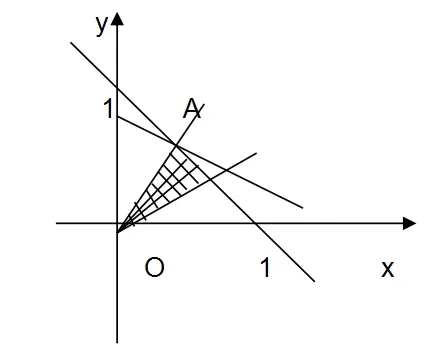
线性规划这部分的题目类型分为三类，只要在直角坐标系中根据其约束条件准确的画出可行域，再按照题目将代数式进行转化，多数转换成纵坐标的最值或者斜率的最值或距离的平方等，然后再进行计算。

二、运用数形结合思想应注意的问题

1．教师在应用数形结合思想应该注意的问题

（1）教师应具备传授学生运用数形结合思想方法解题的教学意识

在明确教学目标的前提下，对教材进行更加深入的钻研。课前充分的准备教案，并设想预期达到的效果。在授课的过程中，对每道例题都进行详细的分析，并归纳总结出哪些题型可以运用数形结合思想，而且在讲授的过程中重点提出，以便帮助学生理解、记忆。在课后，针对数形结合的题目要让学生多做练习，巩固对数形结合思想的认识和掌握。

（2）教师应注重培养学生对“数”与“形”之间的转化

在学生对此部分类型题有所了解的基础上，教师在授课的过程中每当遇到应用数形结合思想的题目就应该给学生巩固加强一遍，来加深学生的印象。这样会让学生达到一种看到题目就会猜想其是否可以应用数形结合思想来解答，达到一种条件发射，这样才可以让学生更好的运用数形结合思想。

（3）教师应注重培养学生的直观思维

授课过程中，教师不要死板的告诉学生其解题方法，而是通过让学生观察、猜想、探讨得出结论。这个过程可以让学生自己创建数学模型，产生直观的视觉效果，从而达到目的。

2．学生在应用数形结合思想应该注意的问题

在运用数形结合思想的过程中，我们发现主要以数轴和直角坐标系为工具进行辅助解题。要想让学生更好的运用数形结合思想大致可分为了解、理解、掌握、灵活运用等几个步骤。在这个过程中对学生的自主学习能力要求较高，因为数形结合的类型题种类很多，这就要求学生要定期的对老师教授的方法进行归纳总结，而且课后要多加练习，巩固知识内容。在巩固练习的过程中，有能力的同学尽量做到对题目进行变式，活稍微修改题目条件看能否继续应用数形结合思想解答，既培养了学生对数形结合思想的应用能力也增强了学生的创新意识。

总之，运用数形结合思想解题，对于学生来说不仅仅是完成一道问题，也会增强学生的认知结构，培养数学思维，提高解题能力和创新能力。尤其对于刚刚走入新课改的我们，有效的利用数形结合思想可以将以往复杂的纯代数进行转化，以繁化简，抽象变具体，在这个过程中让学生体会到数学的乐趣。