浅谈课堂上学生自主学习能力的培养

（汕头市澄海华侨小学 广东 515800）

一、重视观察情境的创设

学习任何知识的最佳途径是由自己去发现，因为这种发现印象最深，理解也最透。因而，在课堂学习中创设恰当的观察情境，训练学生的“观察”能力尤显重要。

1．观察情境创设体现趣味性

课堂上设置趣味的观察情境，能充分调动起学生的学习兴趣，使他们兴致勃勃地去观察、去发现。

例如在三年级“认识周长”一课，教师以小昆虫爬树叶比赛作为趣味情境导入新课。（播放课件：蚂蚁、七星瓢虫、毛毛虫各沿着树叶的边缘爬一圈，谁先到谁赢。） “你觉得谁会是获胜者呢？”有学生说：“是七星瓢虫。”也有学生抢着说：“是毛毛虫。”争议声中还有学生说：“是蚂蚁”。于是课件演示了昆虫爬过的痕迹。“到底谁才是获胜者呢？为什么？”学生会说：“是蚂蚁。”“因为七星瓢虫没有沿着树叶的边缘爬。”“因为毛毛虫只爬了半圈。”……在争议声中学生逐步明白：蚂蚁从一个点开始沿着树叶的边缘爬，最后回到起点，叫做“一圈”。有趣的情境既激起了学生的学习兴趣，又让学生初步感知“边线”和“封闭”，为下面学习周长做好必要的铺垫。

2．观察情境创设体现层次性

三年级下册“数学广角——搭配（二）”的课堂教学中，在学生初步掌握了衣服搭配方法、组内合作完成衣服搭配、独立记录衣服搭配过程之后，教师分别展示学生不同搭配方法的样本：讨论哪一种最优化，为什么？此时所创设的观察情境就富于层次性。

学生自己仔细观察之后，教师提问：你们能看明白是什么意思吗？哪些搭配不重复不遗漏？哪种方法更好？请说一说你观察的结果和收获。

这样，将学生已有知识经验与将要学习的知识联系起来，设置有梯度的、有层次的问题，用设台阶的方法创设观察情境，提高学生学习的整体效益。

3．观察情境创设体现探究性

观察情境富于探究性，能诱发学生的认知冲突，造成学生心理上的悬念，从而唤起学生的求知欲望，激发学习兴趣，把学生带入一种与问题有关的情境中去，进行有效的学习。

如教学“长方形面积的计算”时，在课堂上我先用电脑显示一个长方形房间（长5米、宽3米），让学生观察房间地面上色彩鲜艳的正方形砖块（屏幕上的砖块次序跳跃显示出共15块），然后屏幕下方浮现问题：怎样才能知道房间有多大?我提示学生要解决这个问题可先仔细观察屏幕上的变化：先看清整个房间，然后将房间转变成长方形方框，地面上的方砖也转变成小正方形（图1），再慢慢抽去一部分小正方形，屏幕显示转成图2、图3:

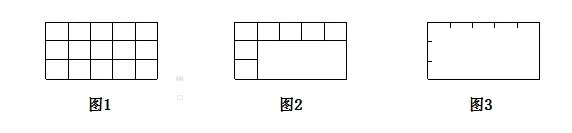
在整个演示过程中，学生先是目不转睛地看，而后很自然地发现了长方形的面积15是由5×3得来，而5是长方形的长，3是长方形的宽，用“长×宽”可求长方形的面积。

二、重视思维过程的表达

课堂上教师应要求学生借助语言，把数学思维过程表达出来。在学生对数学知识能用生活语言叙述出来的基础上，教师随时帮助他们红正错误，补充他们所说的不完整、不全面的部分，并引导用数学语言叙述。从而让学生在表达叙述的过程中更充分地理解知识的内涵。怎样让学生多表达、主动地表达呢，我认为可从以下几点去尝试：

1．多让学生自己讲解。如在学习除数是一位数的口算（69÷3）时，我先让学生单独摆小棒、分小棒，然后在分的过程中自己去思考算法，再把他所想到的口算过程讲给同学听。在学生叙述不完整、表达不准确时我才加以引导、纠正。

2．多让学生自己小结。每一节数学课都有它一定的内容和侧重点，在课末几分钟我经常让学生练习说一说:“这节课你懂得了什么道理?”、“你在哪方面得到了提高?”提问时我还注意分层次，如让能力好的学生先说，有困难的学生听，逐步消化领会后再让他们说，出现问题再请学习好的学生纠正，以提高不同层次学生的说理能力。

3．多让学生起来质疑。例如，我在讲到“0和任何数相乘都得0”这一特征并作板书时，有的学生问道：“老师，什么是任何数呢?”我立即表扬这位同学问得好，能注意观察。因为刚刚升上三年级的学生确实不能确切地理解什么是“任何数”。于是我让学生结合我所举的多个例子，再从语言上稍作引导，有的学生就逐渐地能回答出：“任何数就是所有的数”、“就是从0、1、2、3开始到1千、1万等等的数”。在这个过程中学生对由自己提出并解决的问题印象非常深刻。

4．多让学生互相评价。如学生在说解题思路时，可互相评论，说出其中好的与不好的地方，并讲清理由；或者在校对计算题时，可让学生评价对错，错的怎样改？有的学生对错误分析不到位，需要同学帮忙表达……这样充分发挥评价功能，能促使学生不断地意识自我、发展自我，提高自主学习能力。

三、重视探索过程的思考

学生本身是有个性的，每个人的思维方式也都不同，教师要鼓励学生多动脑筋多思考，学会正确的思维方法。在课堂上我觉得应多留一些时间给学生“想”，并充分肯定他们新颖的想法、独具的见解，使之形成一种氛围。训练学生善于思考的方法表现在课堂中可以是：教师提出了富于探索性的问题；练习题丰富有趣、异于寻常；练习形式自由多样；解决问题的思路多样化，、答案可多个……

如学生在学习了四边形的有关知识以后，为加深学生的系统认识，我认为练习的内容可超越课本，让学生尝试一些异于寻常的题目，从中训练学生的思考能力。具体习题如：下图中哪一个图形是“多余的”？为什么？

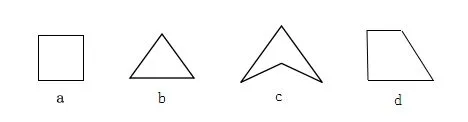
（这道题可以有几种答案：从边数想，b是多余的；从对称性想，d是多余的；从图形特征看，c是凹多边形，，是多余的。）

出示这道题后我让学生分组讨论。由于碰到难题，学生思维活跃，都能认真地在共同讨论中不断比较、判断、异中求佳，思路逐渐拓宽，最后寻求出答案。这样久而久之，能养成学生遇事肯动脑，会思考的好习惯，促进了学生创造性思维的发展，也培养了学生的自主学习能力。

四、重视操作中解决问题

儿章的本性是爱活动，好奇心促使他们什么事都要自己去尝试。我在教学中注重训练学生“做”的能力，让他们在动手操作的过程中独立地去解决问题，学生有时还能于反复摆弄的过程中激起智慧火花，在解决方法上有了自己创新的体验。

例如，在学生熟悉了长、正方形周长的计算之后，课本中出现了这样一道思考题：用四个边长1厘米的正方形摆成下面的图形，哪个图形的周长最短?

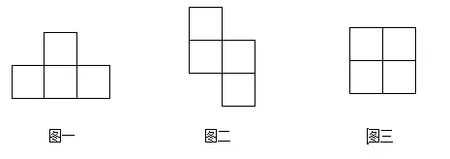
解决这道题时，我没有给学生任何提示，直接就让他们自己动手拼摆来解决问题。刚开始我发现学生大多是按题目的要求，先是拿出学具盒里的小正方形来摆出三个图形，再数一数每个图形外框中所含小正方形边长的总数，从而想出答案（图3周长最短）。于是我告诉学生还可用不同方法来解决，请大家开动脑筋，继续试验，看谁最聪明！在学生继续试着从不同角度去拼、摆、拆、数，反复试验的过程中，出现了以几种情况：（1）有的学生发现可先算出4个小正方形的周长：4×4=16，再减去图形中重复的边长：图1、图2中都有6条边重合，而图3中有8条边重合，依此可知答案。（2）有的学生发现：可用长度一致的小棒把图形的外框摆出来，再数出小棒的根数就可以比较周长了；（3）还有的学生发现可以用“移动、补充”的方法：如把图1平移如下，图2依此类推，与图3就能直接作出比较。学生在反复操作中想出了这样一些方法，有的甚至是老师没有想到的。

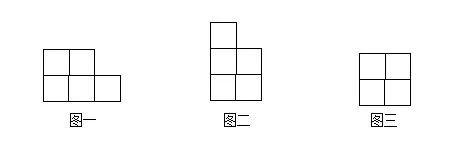
通过实践，我深刻地认识到：学生自主学习能力的培养需要一个很长的过程，在课堂教学中教师应重视学生自主学习能力的培养，充分发挥他们学习的自主性，在观察、表达、思考、操作各项训练中让学生主动地学习、实践、创新，使学习数学真正地变为学生的一种心理需要，使每一节课的学习都成为学生的乐之所在、爱之所在，并从中来促使学生的发展，这才是教学上最大的成功。