散粒体地层土压盾构掘进掌子面稳定性研究

2018-07-20王俊，聂亮，向龙，何川

铁道学报 2018年7期

王俊，聂亮，向龙，何川

(1. 四川省交通运输厅公路规划勘察设计研究院，四川成都 610041；2. 西南交通大学交通隧道工程教育部重点实验室，四川成都 610031)

散粒体介质如砂土、砂卵石、碎石土等是我国城市地铁隧道建设中遇到的典型地质条件，具有离散性强、胶结差及点对点传力等工程特点，对外界扰动反应灵敏。土压盾构在该类地层中施工时，若土仓压力控制不当可能诱发掌子面坍塌，给施工人员、施工机械以及周围环境带来严重威胁。因此，开展散粒体地层土压盾构掘进掌子面稳定性研究对我国城市地铁建设和地下空间的深度开发利用具有显著的工程意义。

目前，国内外学者采用多种手段研究盾构隧道掌子面稳定性。文献[1-4]采用极限理论进行了隧道掌子面稳定性研究，分析时假设了应力场分布(下限理论)或速度场分布(上限理论)。极限平衡理论在隧道掌子面稳定性研究中也得到广泛的运用，该方法需要假定失稳区大小与形状，如对数螺旋曲线[5]、三维楔形体[6-8]以及半球、半圆以及1/4圆[9]等。

文献[10-13]开展模型试验研究了干砂地层中隧道极限支护压力与失稳区分布，探讨了隧道埋深、土体重度等因素对掌子面稳定性的影响规律。文献[14]通过调整螺旋出土器转速探讨了考虑施工扰动条件下砂卵石地层掌子面失稳现象。

数值模拟在隧道掌子面稳定性研究中得到了广泛运用。有限元方面，文献[15]采用PlAXIS研究排水条件下土体内摩擦角对浅埋隧道稳定性的影响，结果表明极限支护压力随内摩擦角的增大而减小。文献[16-17]采用FLAC3D研究考虑渗透力作用条件下盾构隧道掌子面稳定性。离散元[18]方面，文献[19]以马德里地铁隧道为依托工程，使用PFC3D研究黏土地层土压盾构掘进与停机状态下掌子面稳定性等。文献[20-21]采用PFC3D研究了砂土地层土压盾构隧道掘进掌子面失稳现象。

综上所述，采用理论分析、模型试验以及数值模拟等方法研究了盾构隧道掌子面稳定性，研究内容主要集中在极限支护压力以及失稳区分布等方面。由于盾构开挖是十分复杂的刀盘-土体相互作用与力学大变形行为，已有研究基本没有引入盾构动态掘进过程，忽略了影响掌子面稳定性的两个重要因素：盾构刀盘切削土体对地层的扰动效应、刀盘面板对前方土体的支撑作用。前者是诱发地层失稳的重要因素，后者则可以抵挡土体移动，增强掌子面稳定性。文献[14]的模型试验考虑了施工扰动对土压盾构掌子面稳定性的影响，但限于观测手段难以从细观角度解释失稳过程与相应机理，且模型试验需耗费较大的人力物力不易开展参数研究。

鉴于此，采用PFC3D[22]开展了考虑掘进过程的散粒体地层土压盾构掘进掌子面稳定性研究。研究分两步进行：(1)以文献[14]开展的室内试验为基础，建立与之匹配的三维离散元模型，通过对比两者间结果，验证数值方法的合理性；(2)采用验证的数值方法建立原型盾构机模型(D=6.0 m)并在典型散粒体地层中开挖掘进，研究隧道埋深、地层特性以及施工扰动等因素对土压盾构隧道掌子面稳定性的影响规律，并从颗粒运动层面解释隧道失稳机理。

1 土仓压力构建与盾构机建模

1.1 范祚文模型试验简介[14]

范祚文[14]试验中盾构外径D=164 mm，开口率η为50%～70%，刀盘转速Vrot=4 r/min，开挖过程中盾构不向前掘进。模型盾构机土仓后壁安装土压力盒以量测土仓压力，并设置出土口便于人工出土。模型土主要采用中砂、小粒径卵石、重晶石粉和水配制，主要力学参数为黏聚力c=1.97 kPa、内摩擦角φ=43.1°，压缩模量Es=12 MPa，试验相似比为38.75。模型试验中刀盘转动切削开挖面土体并使其进入土仓，通过人工出土降低土仓压力模拟支护压力不足时开挖面失稳过程。

1.2 土仓压力构建

土压盾构掘进过程中千斤顶推力通过承压隔板传递给土仓内的渣土，渣土压力作用在掌子面上以抵抗前方水土压力，当两者平衡时开挖面稳定。文献[23]认为土仓隔板处的土压力小于开挖面处实际土压力，两者之间存在传递系数，该系数受开口率等因素影响变化规律复杂。简便起见，实际运用时该参数一般按经验取值，如文献[14]在处理试验数据时该系数取为1.1。故研究隧道稳定性时，若能直接得到掌子面处极限支护压力以避免选取传递系数更加合理。土压盾构施工时需要向渣土中注入添加剂提高渣土的流塑性。改良后的渣土具有良好的流塑性不能受剪，故其对隧道的支撑效应可视为作用在掌子面上的法向力，可将渣土-掌子面土体相互作用简化为三维应力边界问题。

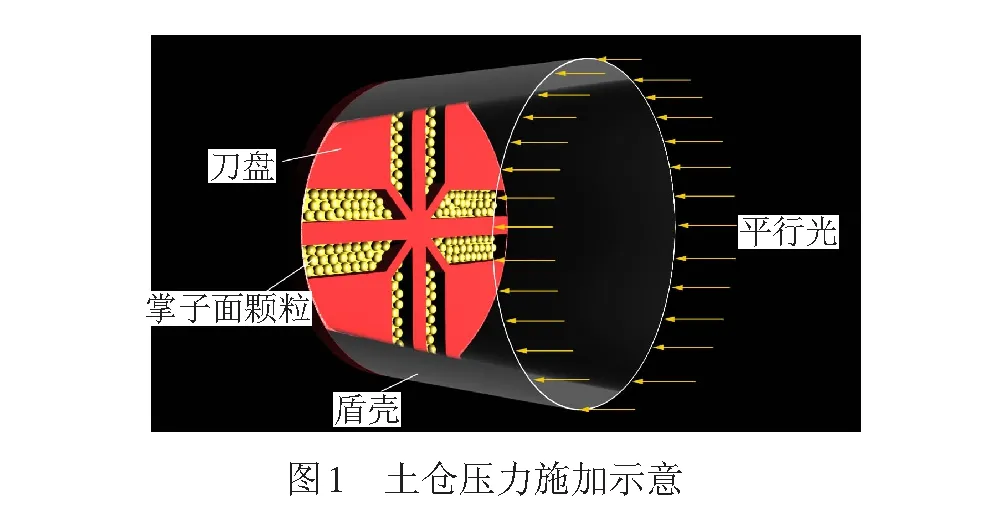
采用PFC3D内置的Fish语言进行编程[22]，将土仓压力对掌子面的支护效应抽象成作用在掌子面颗粒上的指定压力，构建上述应力边界。假设盾构机体正后方存在一束射向掌子面的平行光，所有能接收到光照的颗粒即为掌子面颗粒，颗粒所受的支护力与光照面积成正比，见图1。程序具体实现时，假设在盾构机正后方存在一个边长与盾构直径相等的平面，并对其进行离散化处理，得到一系列晶格，所有的颗粒均沿隧道轴线向离散晶格投影，得到该方向上距对应晶格最近的所有颗粒(即掌子面颗粒)，再根据颗粒在对应晶格上的投影面积Ap给掌子面颗粒施加指定的支护力f=pAp(p为仓内支护压力，kPa)。引入该三维动态柔性应力边界可极大地简化研究过程，数值模型只需考虑盾构的掘削系统而不需要考虑渣土改良、螺旋出土器等其他系统，且能给掌子面颗粒施加任意指定的土仓压力，精确研究土压力对掌子面稳定性的影响。

1.3 土压盾构建模

为了比较数值模拟与模型试验结果，建立与室内试验相匹配的盾构机数值模型。由于盾构机体刚度大，采用wall单元对其进行模拟。若采用逐个输入wall单元顶点的方法生成目标盾构机模型耗费大量时间且易出错。为提高建模效率采用以下步骤生成盾构机模型：

Step1在CAD软件中(如Rhino、Solidworks、Pro/E等均可)建立目标盾构模型；

Step2将建好的模型另存为.stl格式文件；

Step3在PFC3D中调用CAD_support.fis文件生成盾构机，并施加指定的施工参数模拟土压盾构开挖。该方法充分利用了CAD技术建模效率高的优点，能快速精确得到目标模型。

2 数值模型合理性验证

2.1 细观参数标定

采用三轴试验对模型试验土进行标定，试样应力-应变曲线见图2(a)。标定时同样采用三维柔性应力边界有效模拟室内试验中橡皮膜对试样的柔性约束，消除了传统数值三轴试验中刚性wall单元对土体侧向不均匀变形的限制，最终剪切破坏的试样见2(b)，标定好的细观参数见表1。

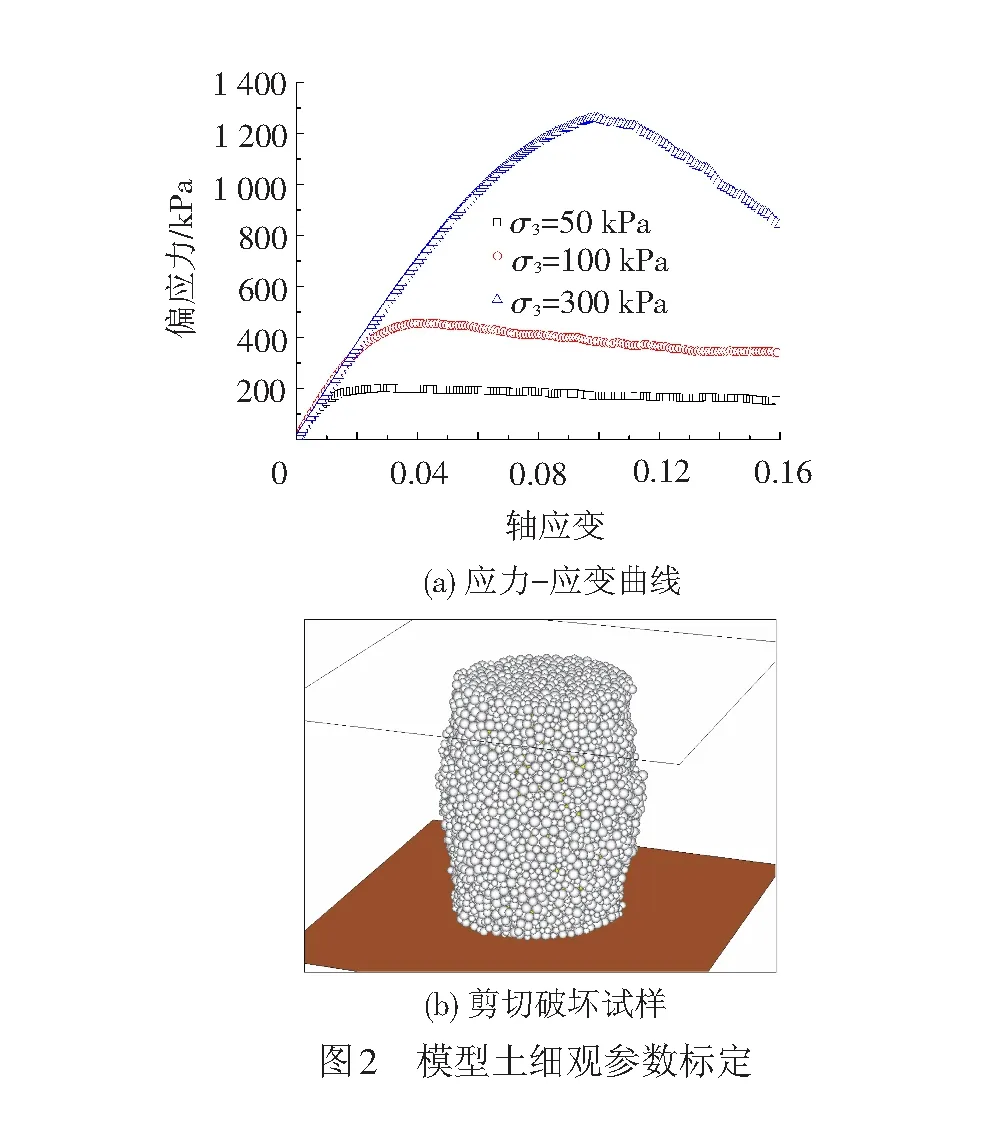
表1 模型土地层细观力学参数

2.2 PFC3D数值模型

数值模型尺寸为长×宽=1.5 m×1.2 m，高度由隧道埋深确定，与室内模型试验相同考虑了C/D为0.5、1.0两种埋深工况，隧道直径D=0.16 m。

数值模拟分以下几个步骤进行：

Step1根据标定的细观参数，采用“落雨法”分层生成地层模型，在重力作用下完成固结后删除地层顶部少量浮皮颗粒。

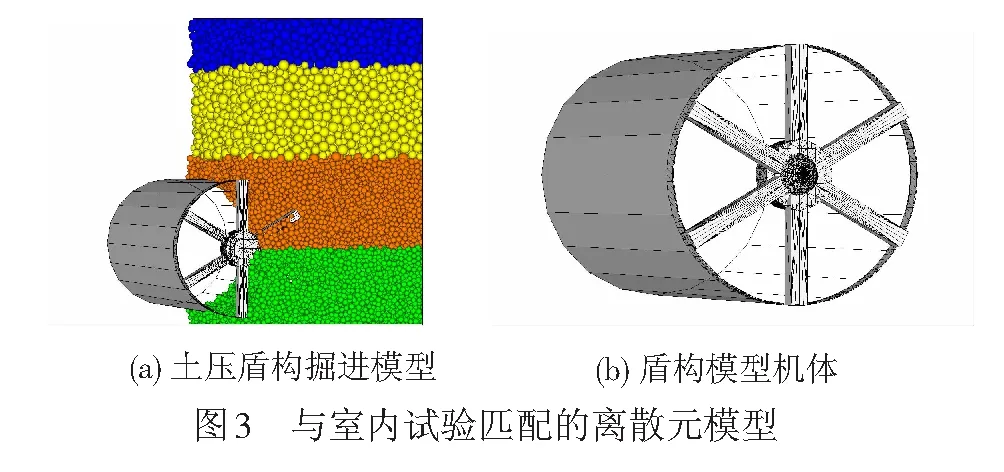
Step2在指定范围内删除地层颗粒并采用前述方法生成盾构模型，见图3。盾构刀盘与模型试验基本一致，开口率为60%。开挖过程中刀盘转速为4.0 r/min与试验相同且不向前掘进。

Step3采用前述方法识别掌子面颗粒，并施加与隧道轴线处静止土压力相等的初始支护压力，此后分步等量减少该支护压力直至0 kPa，同时密切监控掌子面前方土体位移变化，当地中测点位移突然增大时，可认为此时的支护压力为掌子面极限支护压力[10, 15]。

2.3 数值模型合理性验证

通过将数值模拟得到掌子面极限支护压力与失稳区分布并与室内试验结果进行对比,验证其合理性。C/D为1.0、2.0时典型测点沉降与土仓压力关系曲线见图4，典型测点位于隧道拱顶正前方0.02 m(1/8D)，由文献[10-15]知该点位于隧道失稳区核心部位，能及时反映地层失稳情况。

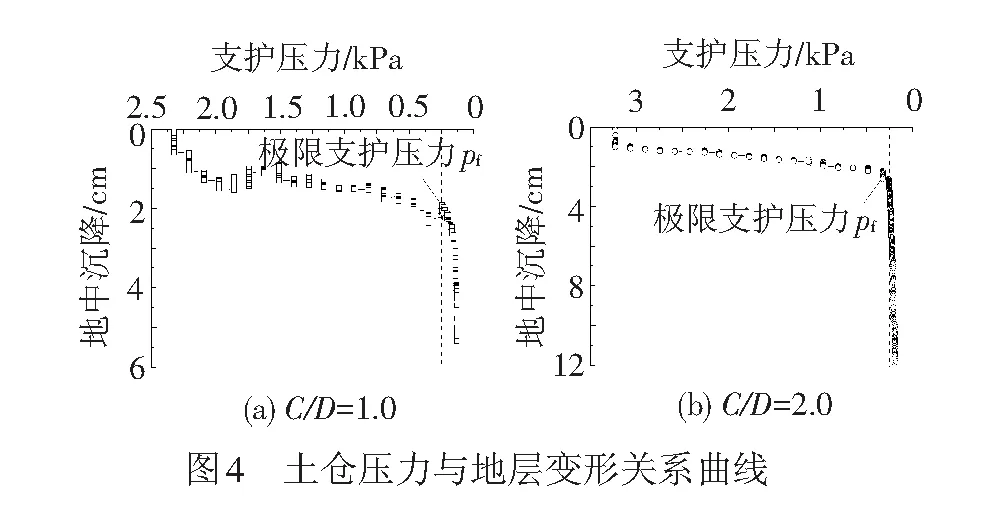
由图4可见，C/D为1.0、2.0时极限支护压力pf分别为0.25、0.32 kPa，相应的室内模型试验[14]结果为0.259 8、0.322 1 kPa，可见两者之间非常接近，可以验证数值模型的合理性。

为得到失稳区分布，研究了地层变形情况。典型横断面方向地层变形情况见图5，根据文献[21]研究可知，散粒体地层中可以通过地层沉降位移梯度判定失稳区分布，连接所有位移突增点即可得到失稳区。

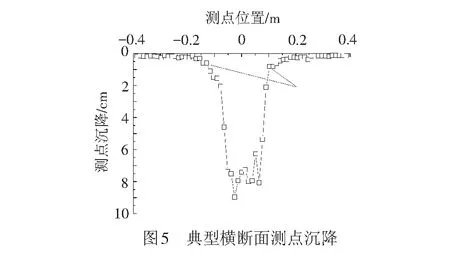
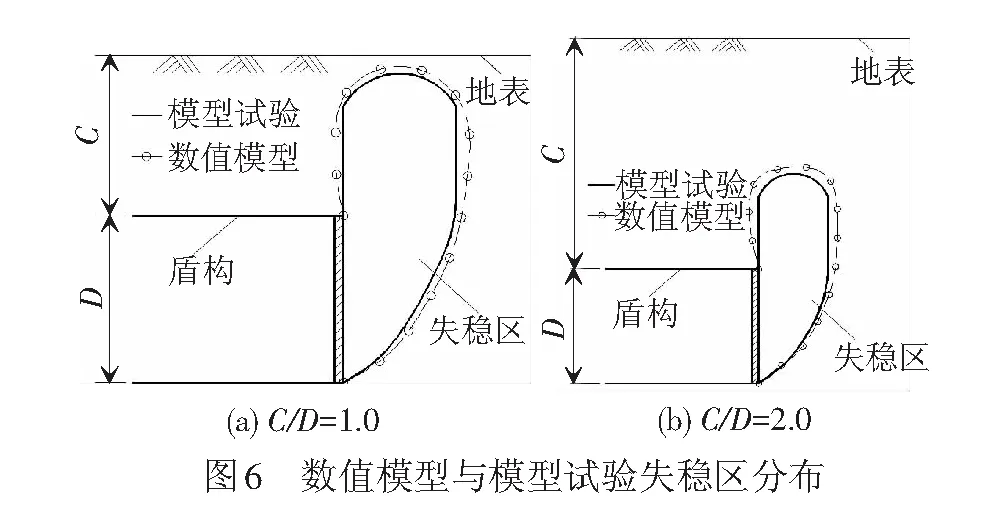
采用上述方法得到C/D为1.0、2.0时失稳区分布情况，见图6。数值模型得到的失稳区分布范围与模型试验吻合良好，前者略大于后者且向掌子面后方发展一段范围，但均未发展至地表。综上所述，数值模拟得到的掌子面极限支护压力和失稳区分布均与室内模型试验吻合较好，可以验证其合理性。

3 散粒体地层盾构掘进稳定性

土压盾构在工程性质迥异的散粒体地层中掘进时引起的地层扰动不尽相同，需要区别对待[15]。鉴于此，采用前述验证过的数值方法建立原型盾构(D=6.0 m)并在典型散粒体地层中开挖掘进，探讨了土体特性、隧道埋深、施工扰动等因素对土压盾构掘进稳定性的影响规律，并从颗粒运动层面解释隧道失稳机理。选取3种典型散粒体地层，其物理力学参数见表2。

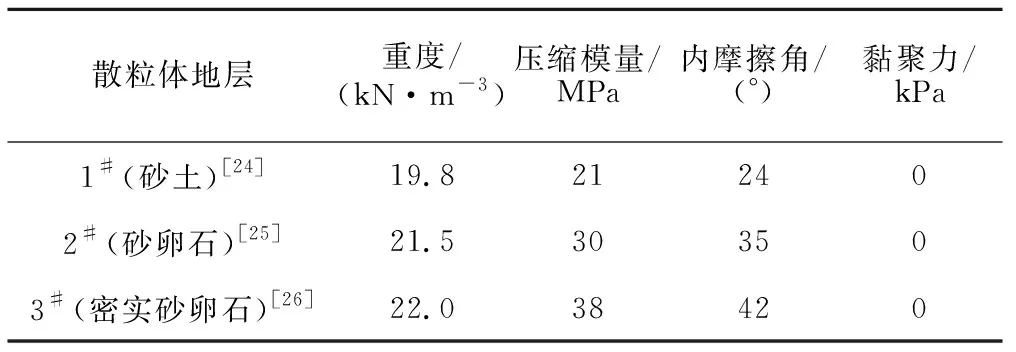
表2 典型散粒体地层力学参数

采用前述的三轴试验对以上3种散粒体地层均进行了标定，最终采用的细观参数见表3。

表3 散粒体地层细观力学参数

数值模型建立过程与2.2节基本相同，每种地层均考虑了C/D为0.5、1.0、2.0、4.0 四种埋深。盾构刀盘采用散粒体地层中土压盾构开挖常用的面板辐条形结构，由于工程中盾构面板开口率不尽相同，为减少分析变量，数值模型中土压盾构面板开口率统一取为40%，面板最小开口尺寸dop=1.20 m，dop/dmax≈4.5(dmax为砂土颗粒的最大直径)，由文献[19]知dop/davg≥3(davg为砂土颗粒的平均直径)即可确保砂土颗粒顺利进入土仓。刀盘共布置72把刮刀，并在面板中心布置一把鱼尾刀，面板开口与刀具布置详细情况见图7。开挖过程中掘进速度Vtrs=3.5 cm/min，刀盘转速Vrot=1.5 r/min，整个模拟过程中施工参数维持不变。

为监控地层位移，地中与地表测点的布设见图8。

3.1 极限支护压力

采用2.3节方法得到所有研究工况的极限支护压力，见图9。总体来讲，砂卵石地层(2#地层)中极限支护压力大于砂土地层(1#地层)但小于密实砂卵石地层(3#地层)，呈现出内摩擦角越大隧道掌子面极限支护压力越小的趋势，与Vermeer等[15]研究结论一致。此外，对砂土与砂卵石地层，极限支护压力随隧道埋深增加呈线性增长，而密实卵石土地层中C/D≤2.0时极限支护压力随埋深小幅度增加，此后基本不再变化。

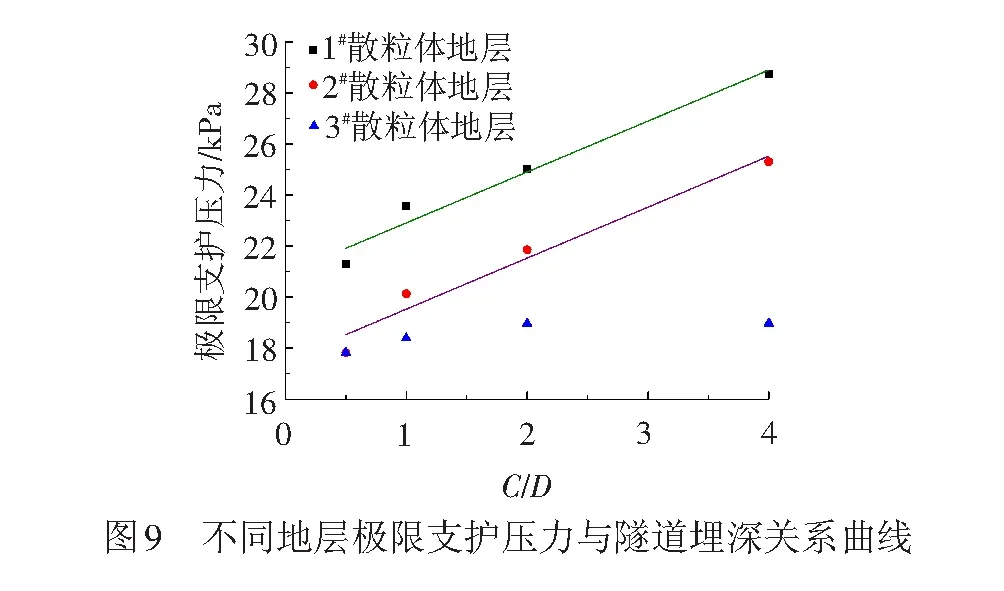
定义支护压力比η=p/p0，其中，p为支护压力，p0为初始支护压力。所有工况的极限支护压力比ηf见表4。由表4可见，极限支护压力比随隧道埋深与土体内摩擦角增加而减小。

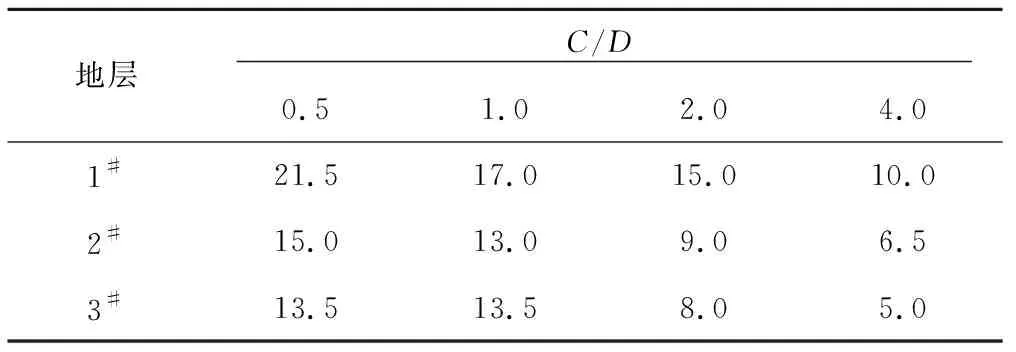
表4 掌子面极限支护压力比 %

3.1.1 与已有研究比较

以2#地层为例，引入无量纲参数pf/γD将离散元计算结果与理论研究和模型试验进行了对比，见图10。由图10可见，离散元模型得到的掌子面极限支护压力大于其他研究结果，出现该结果的可能原因是离散元分析中考虑了盾构掘进过程，刀盘不断切削土体，迫使土颗粒随刀盘转动破坏地层原有结构诱发掌子面坍塌，而既有理论分析[1-9]或应力、应变控制的模型试验[10-13]均没有考虑外界施工扰动对稳定性的影响，此时开挖面失稳实质是土体抗剪能力不足引起地层滑移的力学行为。

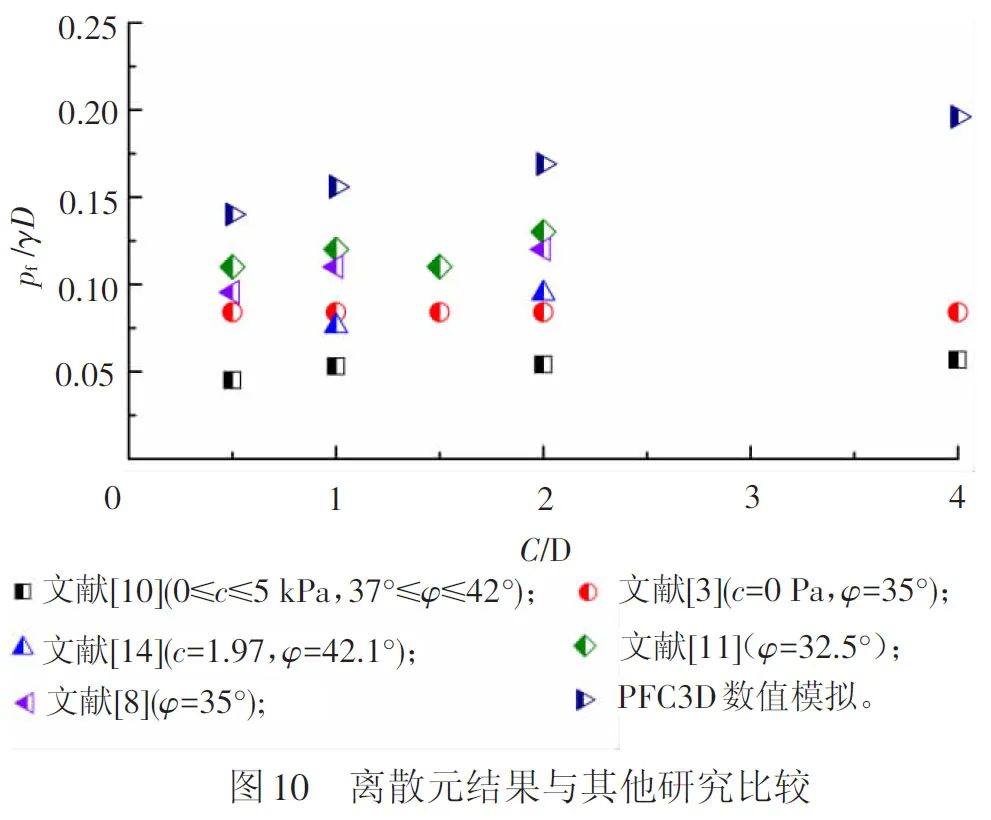
此外，离散元计算结果也大于文献[13]的模型试验，主要原因有3点：(1)2#地层的内摩擦角小于模型试验，由文献[15]研究可知，极限支护压力随土体内摩擦角增大而减小；(2)2#地层没有黏聚力，理论研究认为[2-3]，黏聚力的存在可以加强土体自稳能力，有效减低极限支护压力；(3)与室内模型试验不同，离散元模型中刀盘配备了刮刀与鱼尾刀更加接近实际工程，刀盘旋转时刀具切削土体对地层的扰动作用更大。

3.1.2 掘进过程对极限支护压力的影响

以2#地层为例，定量研究刀盘切削土体与面板支撑对稳定性的影响，研究过程见图11。

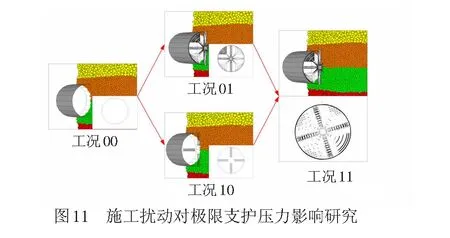
每种埋深均考虑4种工况：不考虑面板支撑也不考虑刀盘切削土体(工况00)，该工况可对应Chambon模型试验[10]；考虑刀盘支撑但不考虑刀盘切削土体(工况01)，该工况可研究安装管片和刀具维护等停机状态时掌子面稳定性；考虑刀盘切削土体但不考虑刀盘支撑(工况10)，刀盘只配备刀具没有面板，开口率接近100%；既考虑刀盘切削土体也考虑刀盘支撑(工况11)。4种工况下的计算结果见表5。由表5可见，施工扰动削弱地层的稳定性，掌子面极限支护压力增大，挡板支撑则会增强地层自稳性，减小极限支护压力。

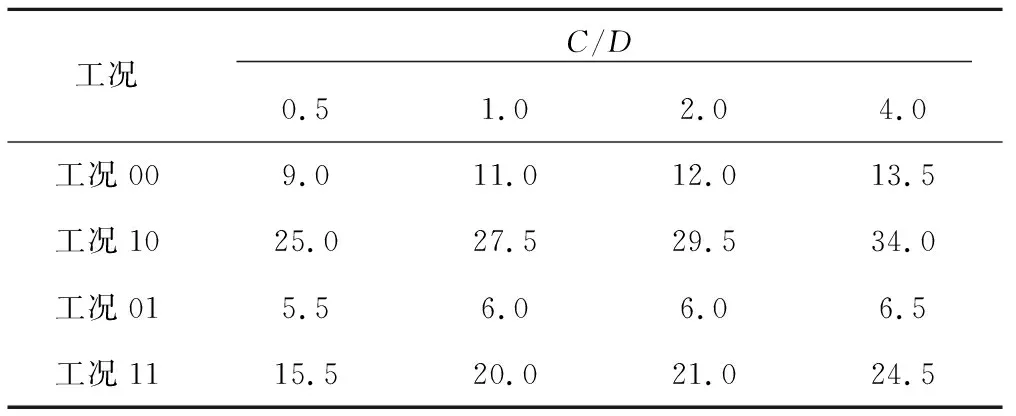
表5 不同工况下极限支护压力 kPa

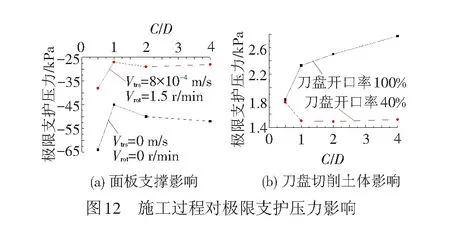
定量分析了面板支撑与刀盘旋转切削土体对极限支护压力的影响规律，见图12(a)。考虑施工扰动时极限支护压力变化率λ=(pf11-pf10)/pf10，不考虑施工扰动时λ=(pf01-pf00)/pf00，pfij为对应工况极限支护压力，其中i，j=0，1。不同施工参数下面板支撑对λ的影响规律基本相同，但盾构掘进时λ变化幅度大于停机状态。C/D=0.5时面板支撑对pf影响最大，随着埋深增大λ减小并最终趋于稳定。研究盾构掘进施工对极限支护压力的影响规律见图12(b)。面板开口率为40%时极限支护压力变化率λ=(pf11-pf01)/pf01，开口率为100%时极限支护压力变化率λ=(pf10-pf00)/pf00。不同开口率时盾构掘进对λ的影响规律不同，开口率为100%时，随埋深增加λ不断增加，C/D=0.5～1.0变化幅度最大，此后增长趋缓；开口率为40%时，C/D=0.5～1.0过程中，λ迅速降低，此后基本不再变化。

3.2 失稳区分布

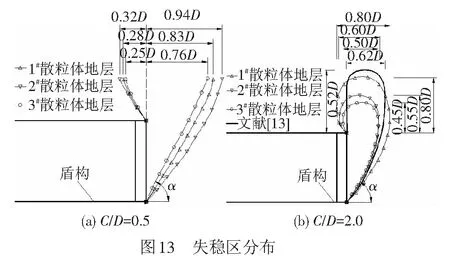
支护压力p=0 kPa时C/D为0.5、2.0的失稳区分布分别见图13。由图13可见，隧道失稳区从拱脚与拱顶发展，具体形态受埋深与土体内摩擦角影响。C/D=0.5时，由于覆土过浅，拱顶上方没有形成塌落拱，隧道失稳区均发展到地表，掌子面前方延伸范围随内摩擦角增大而减小， 1#、2#、3#地层分别为0.94D、0.83D、0.76D，此外失稳区还向隧道掌子面后方发展一定距离，延伸范围也与地层内摩擦角相关。拱脚处失稳区轮廓与水平方向夹角α分别为58°、63°、70°，约等于(45°+φ/2)，φ为土体内摩擦角。C/D=2.0时，失稳区没有发展至地表。内摩擦角越大，失稳区范围越小，3种地层失稳区向拱顶上方分别发展了0.45D、0.55D、0.80D，α分别为56°、62°、68°，与C/D=0.5工况基本相等。由于数值模型中的刀盘开口率为40%小于室内模型试验(50%～70%)，失稳区范围也相应小于模型试验。

3.5 隧道失稳细观机理研究

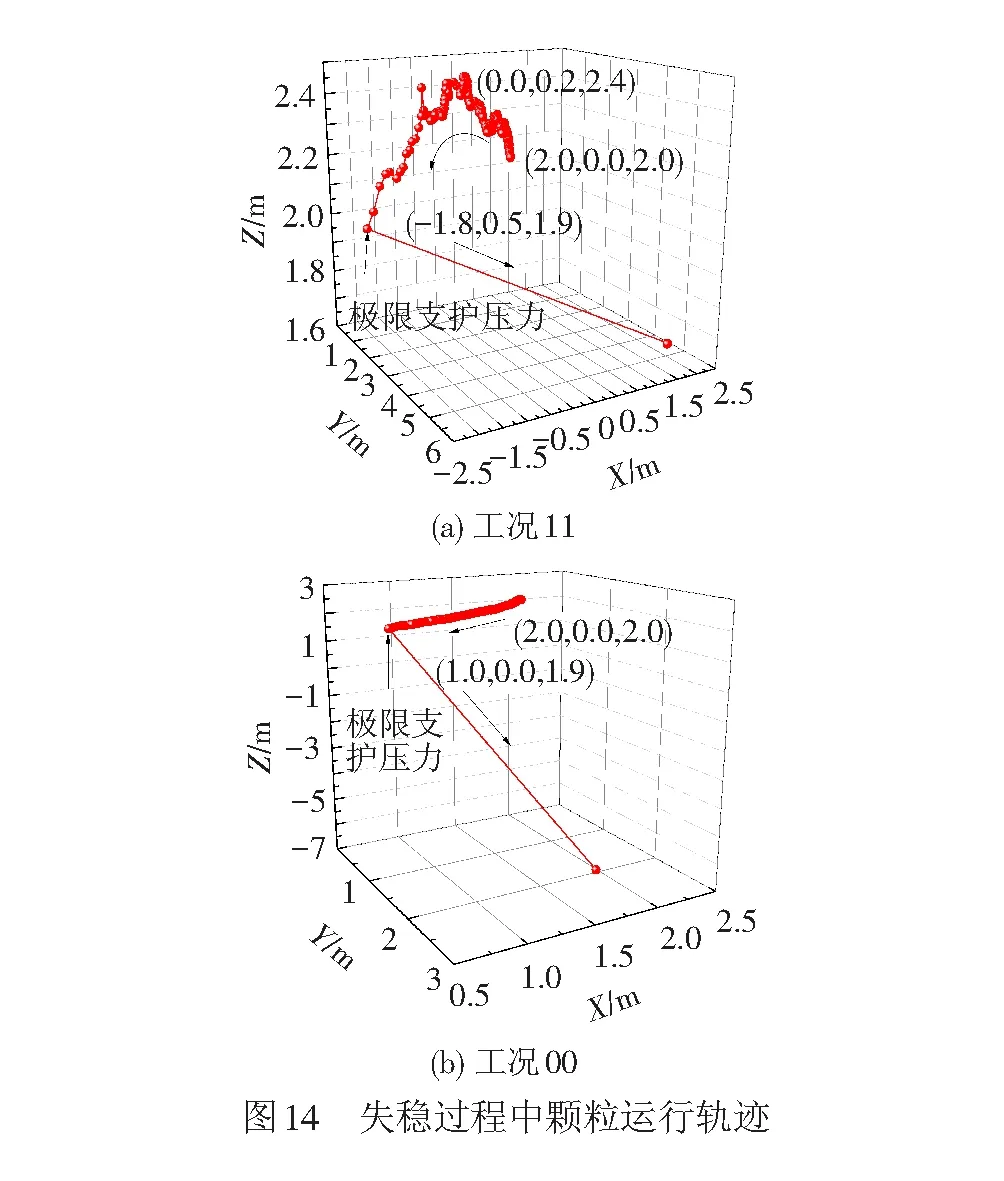
掌子面前方典型位置处(2，0，2)隧道失稳过程中颗粒三维运行轨迹见图14。由图14(a)可见，考虑施工扰动时土颗粒随刀盘运动，发生绕隧道轴线旋转的圆周运动，随支护压力的减小，有沿z方向流向隧道内部的趋势，当支护压力降至pf时，颗粒突然涌进土仓，隧道随之失稳。隧道失稳前该土颗粒在xz平面内发生了较大的被动位移，位置变化剧烈，x方向位移为3.8 m，z方向先随刀盘向上运动，再向下运动。刀盘切削土体破坏了掌子面附近土体原有结构，地层变的松散，由于散粒体地层本身无黏聚力，隧道自稳性主要由土颗粒间的摩擦力提供，故隧道稳定性被大幅度削弱。不考虑施工扰动影响时(工况00)同一土颗粒的运行轨迹见图14(b)，由图14(b)可知，此时颗粒运行轨迹比较简单与考虑施工时差异明显，颗粒主要发生向隧道轴线的收敛位移，当支护压力降为pf时，土颗粒涌进土仓，隧道失稳。