基于样本信息重构的小子样P-S-N曲线拟合方法

刘文飞， 刘志明， 薛 海， 贾裕祥

(1. 北京交通大学 机械与电子控制工程学院， 北京 100044； 2. 包头北方创业有限责任公司， 内蒙古 包头 014032)

概率疲劳寿命曲线(以下简称P-S-N曲线)是进行结构疲劳可靠性设计与评定的基础。利用疲劳试验数据拟合高精度的P-S-N曲线是疲劳研究者与统计学者长期关注的重点之一[1]。根据抽样理论，试验样本量越大，试验评估准确度就越高，越能够真实地反映产品质量水平[2]。但由于疲劳试验成本高且耗时长等条件的限制，一般情况下很少能满足抽样理论中大样本数据的要求，尤其对于尺寸较大的结构件或比较贵重的零部件只能基于小子样或极小子样进行疲劳寿命统计推断。目前国内外学者对基于小子样的结构疲劳寿命统计推断进行了相关研究，如在舰船、航空、铁路等领域基于小子样疲劳试验数据采用贝叶斯方法进行疲劳寿命评估[3-5]，拟合S-N曲线时常采用最小二乘法、极大似然法、异方差理论等方法与理论[6-7]，也有采用现代智能算法与其他算法相结合的方式对小子样进行寿命评估[8-9]。此外，国家标准中金属材料疲劳试验数据统计方案与分析方法也给出了小子样疲劳试验数据的处理方法[10]。但上述研究尚未提及样本的疲劳寿命标准差与应力水平变化规律不惟一时的处理方法，而此现象在零部件疲劳试验中时有发生。

本文基于中寿命区对数疲劳寿命分布规律与寿命等效原理，针对小子样的疲劳寿命标准差与应力水平整体呈近似线性关系，但在部分应力水平下不呈线性关系时，提出了样本信息重构方法，有效降低了部分应力水平下小样本与异常样本对疲劳寿命均值与标准差的影响，确保样本疲劳寿命等效转换的精确度，并通过与寿命等效原理相结合，最大限度地应用了疲劳试验信息，形成了基于样本信息重构并符合疲劳寿命等效原理的极大似然法与基于样本信息重构的最小二乘法，通过应用疲劳试验数据对本文提出的两种方法与传统的极大似然法与最小二乘法进行对比分析，最终确定了基于小子样试验数据拟合高精度P-S-N曲线的方法。

1 基于样本信息重构的寿命等效原理

1.1 S-N曲线数学表达式

S-N曲线代表了材料的疲劳性能，通常用数学表达式来描述其规律。对于金属材料，在中寿命区的S-N曲线可用幂函数形式表示，即

SmN=C

( 1 )

式中：S为应力水平；N为在S应力水平下材料的寿命；m、C是与材料、应力比、加载方式等有关的参数，由试验确定。

对式( 1 )两端分别取对数，则有

lgN=lgC-mlgS

( 2 )

令

X=lgSY=lgNA=lgCB=-m

( 3 )

可得

Y=A+BX

( 4 )

由式( 4 )可知，疲劳寿命N与应力水平S在对数坐标系中呈线性关系。

1.2 基本假设

大量的疲劳试验已证实，在中寿命区对数疲劳寿命一般遵循正态分布[7]。假设试验有n个应力水平，试样总数为m，第i个应力水平下的试样数为mi，第i个应力水平下的第j个试样的疲劳寿命为Yij，结合式( 3 )，其概率密度函数为

( 5 )

式中：i=1,2,…,n；j=1,2,…,mi；μi与σi分别为试样在第i个应力水平下的对数疲劳寿命均值与标准差。

其概率分布函数为

( 6 )

1.3 疲劳寿命等效原理

由式( 1 )可知，当加载方式、应力比、载荷形式，以及试验方法等确定后，在指定应力水平下，试样的寿命受材料自身性能与试样加工质量等因素的影响。在试验过程中，虽然无法实现对同一试样在不同应力水平下进行疲劳试验，但是由“寿命概率分位点一致性原理”[11]可知，在中寿命区范围内，同一试样在不同应力水平下其寿命具有相同的概率分布，即同一试样在不同应力水平下的疲劳寿命概率分布F(Yij)恒定，结合式( 6 )可得

( 7 )

式中:T为常数。

由式( 7 )可知，根据各应力水平下的对数寿命的均值与方差，可实现同一样本的疲劳寿命可以在不同应力水平下相互等效，此方法可根据现有试验样本，增加不同应力水平下的样本数量，最大限度地利用了试验全部样本信息，特别为小子样在不同应力水平下的样本扩展提供了较好的方法。但此方法是基于可获得各应力水平下精度较高的寿命均值与标准差，而寿命均值和标准差分别与应力水平存在着一定的内在联系，因此找出其较理想的对应关系尤为重要。

1.4 寿命均值与应力水平关系的确定方法

在第i个应力水平下试样的疲劳寿命均值计算方法为

( 8 )

由式( 4 )可知，在中寿命区疲劳寿命与应力水平相关，且大量试验表明，试验样本的寿命均值与应力水平在对数坐标系下有较好的线性对应关系，可采用最小二乘法进行拟合，即使在个别应力水平下存在极小子样的情况，也可保证中值S-N曲线的拟合精度。

1.5 寿命标准差与应力水平关系的确定方法

为了获得P-S-N曲线，疲劳试验通常采用升降法在4～5个应力水平下进行，对于可靠性试验一般在每个应力水平下需要15个样件，但是即使在试验控制的非常精确的时候，疲劳试验结果也有可能出现较大的差异。这种差异部分来自于试样的化学成分、热处理、表面状态等的不一致性，部分来自于工程材料的内禀特性——疲劳失效的随机过程[10]。一般用方差或标准差代表样本的分散度，标准差计算方法为

( 9 )

在小子样或极小子样的情况下，试验数据分布情况很难准确地说明真实分布情况，甚至有可能出现与真实分布相悖的情形。例如，虽然对数寿命标准差与对数应力水平在整体上呈线性关系，但在部分应力水平下，存在低应力水平的寿命标准差比高应力水平的寿命标准差小的情形，与一些学者认同的线性异方差理论或同方差理论相悖[12-13]。为了遵循不同材料的自身特性，本文给出了3种不同情形下应力水平与标准差关系的确定方法。

(1) 当不同应力水平下对数寿命标准差与对数应力变化规律近似呈线性关系时，可采用线性异方差理论或最小二乘法进行拟合。

(2) 当不同应力水平下对数寿命标准差近似相等时，可将不同应力水平下对数寿命标准差求均值后作为各应力水平下的标准差。

(3) 当寿命标准差与应力水平的变化规律不惟一时，可采用样本信息重构方法对试验数据进行处理，然后采用最小二乘法拟合重构后的应力水平与标准差的关系曲线。

1.6 样本信息重构方法

大量试验结果显示，在中寿命区绝大部分金属材料的对数寿命标准差与应力水平近似存在线性关系[14]，但在试验中常常会发生部分高应力水平下寿命标准差比低应力水平下寿命标准差大或相等的情形，因此本文重点给出样本的对数寿命标准差与对数应力水平整体呈线性关系，但在部分相邻的应力水平下不呈线性关系时的处理方法，具体方法如下：

当相邻的2个应力水平下的对数寿命标准差随对数应力水平变化的趋势与整体变化趋势不一致时，将2个应力水平合并为1个应力水平，在新的应力水平下有

(10)

当相邻的3个应力水平下的对数寿命标准差随对数应力水平变化的趋势与整体变化趋势不一致时，将3个应力水平合并为1个应力水平，在新的应力水平下有

(11)

2 基于小子样P-S-N曲线拟合方法

对于1.5节中基于前2种情形时的P-S-N曲线拟合，国内外学者已给出较多的处理方法，且基本已有定论。本文针对当寿命标准差与应力水平的变化规律不惟一的情形，提出了2种拟合P-S-N曲线的方法，分别为：基于样本信息重构并符合疲劳寿命等效原理的极大似然法与基于样本信息重构的最小二乘法，最终通过应用疲劳试验数据对2种方法进行对比分析，选出了1种拟合精度较高且偏于安全的方法。

2.1 极大似然法拟合P-S-N曲线的基本原理[15]

极大似然法测定疲劳性能曲线时，首先在每个应力水平Si下分别使用一个试样进行试验，相应的对数疲劳寿命为Yi，然后在某一指定应力水平Sd下，试验一组试件，获得q个对数疲劳寿命观测值Ydj(j=1,2,…,q)，同时在中等寿命区线段，采用2个假定：对于各级应力水平，对数疲劳寿命都遵循正态分布；正态母体平均值和母体标准差均与对数应力水平成线性关系，即

μi=μd+αXi-Xd

(12)

σi=σd+βXi-Xd

(13)

式中：Xi、Xd分别为Si与Sd在对数坐标系下的值；μd与σd分别为试样在应力水平Sd下的对数疲劳寿命均值与标准差；α、β是待定常数。

破坏概率为p的对数疲劳寿命为

Yp=μ+upσ

(14)

根据上述假定，似然函数可写为

(15)

将式(12)、式(13)代入式(15)，并且两边取自然对数可得

当lnL达到最大值时，对应的α、β就是参数α、β的极大似然估计；或对上式分别求α、β的偏导，并分别令其为零，也可求出α、β的值，即

通过上述方法可得出P-S-N曲线方程为

Yp=μd+upσd+(α+upβ)(Xi-Xd)

(16)

2.2 基于样本信息重构并符合疲劳寿命等效原理的极大似然法

本文提出的极大似然法是将样本信息重构与寿命等效原理相结合，提高样本寿命标准差的准确度，保证寿命等效的精度，最终采用极大似然法对等效后的数据进行P-S-N曲线拟合，具体步骤为：

Step1根据1.4节的寿命均值与应力关系的确定原则拟合出对数应力水平与对数寿命均值直线，然后通过该直线计算出不同应力水平下的寿命均值。

Step2根据1.5节中给出的第(3)种方法计算出各应力水平下的寿命标准差。

Step3根据寿命等效原理，结合Step1与Step2得出的寿命均值与标准差，将不同应力水平下的疲劳寿命等效到特定的应力水平下，一般以样本数量较多的应力水平确定为特定应力水平，实现疲劳寿命在不同应力水平下的等效。

Step4采用极大似然法对等效后的数据进行P-S-N曲线拟合。

2.3 基于样本信息重构的最小二乘法

最小二乘法对各应力水平下的样本数量无特殊要求，因此本文提出的基于样本信息重构的最小二乘法无需进行寿命等效，具体拟合步骤为：

Step1根据2.2节中的Step1与Step2得出样本重构后各应力水平下的寿命均值与标准差。

Step2通过式(14)，计算出不同应力水平下破坏概率为p的对数寿命Yp。

Step3采用最小二乘法对不同应力水平下的对数寿命Yp进行拟合，得出P-S-N曲线。

3 算例分析

为了验证本文提出的基于小子样的P-S-N曲线拟合方法的精度，本文对切割光滑板材T型接头的Q450NQR1试样进行疲劳试验，加载方式为轴向拉-拉循环，应力比R=0.1，正弦波加载，加载频率为70 Hz左右，寿命循环数控制在105～2×106之间，采用升降法进行试验[16]，试验数据见表1。

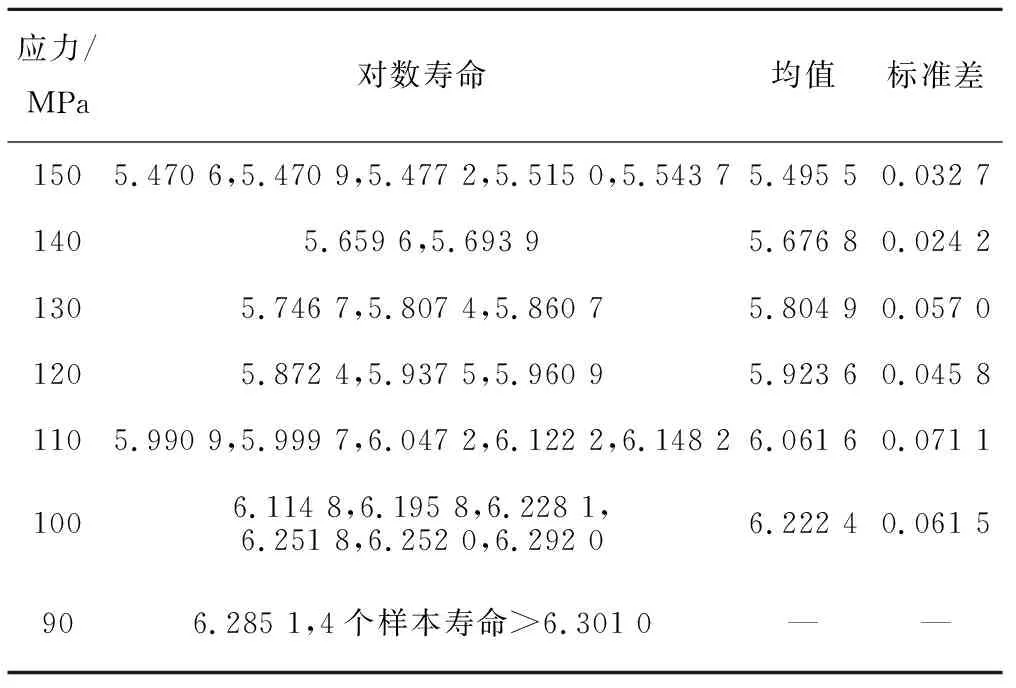
表1 Q450NQR1疲劳寿命试验数据

采用1.4节的确定原则对表1中的试验数据进行分析处理，拟合后的样本寿命均值与应力水平的关系为

Xi=3.555 5-0.249 4μi

(17)

采用1.5节中的第(3)种方法对相邻2个应力水平下的样本信息进行重构，重构后的应力水平与标准差见表2，拟合后的寿命标准差与应力水平的关系为

σi=0.548 4-0.238 4Xi

(18)

同时根据式(17)可得出重构后的应力水平对应的寿命均值见表2。

表2 样本信息重构后的寿命均值与标准差

3.1 极大似然法拟合P-S-N曲线

根据式(17)与式(18)，可得出各应力水平下的寿命均值与标准差，见表3。

表3 拟合后的寿命均值与标准差

试验数据在110 MPa应力水平下的样本数量相对较多，且比100 MPa应力水平更接近其他应力水平，因此选110 MPa为特定应力水平。

根据1.3节中的寿命等效原理，将表1中试验数据直接进行寿命等效，等效后的数据见表4。

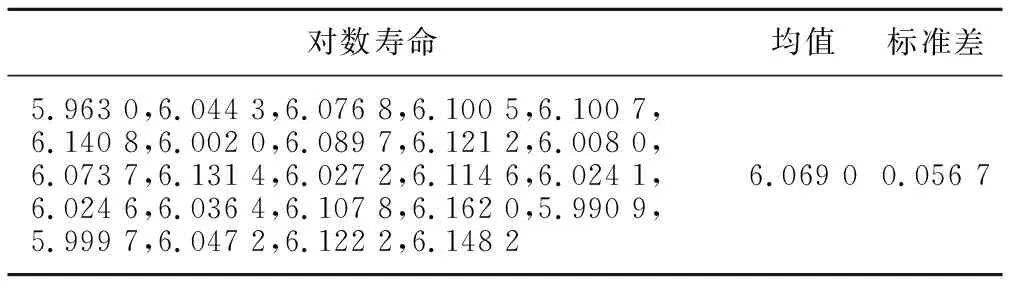
表4 试验数据的等效寿命

将表1中的对数寿命与表3中的所有数据进行寿命等效，等效后的数据见表5。

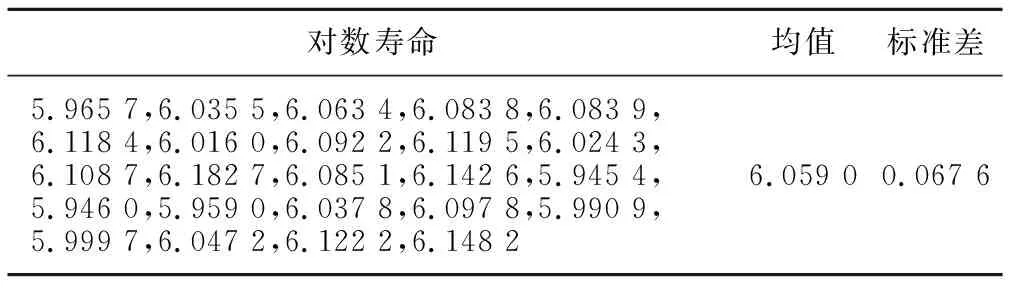
表5 样本信息重构后的等效寿命

采用极大似然法对表1与表4中的数据进行分析处理，拟合后的P-S-N曲线称为极大似然法1，数学表达式为

Yp=6.069 0+0.056 7up-

(3.839 6+0.177 8up)(Xp-2.041 4)

采用极大似然法对表3与表5中的数据进行分析处理，拟合后的P-S-N曲线称为极大似然法2，数学表达式为

Yp=6.059 0+0.067 6up-

(3.930 5+0.277 2up)(Xp-2.041 4)

根据以上给出的2种拟合方式，分别拟合存活率p为50%、90%、99.9%时的P-S-N曲线，见图1。

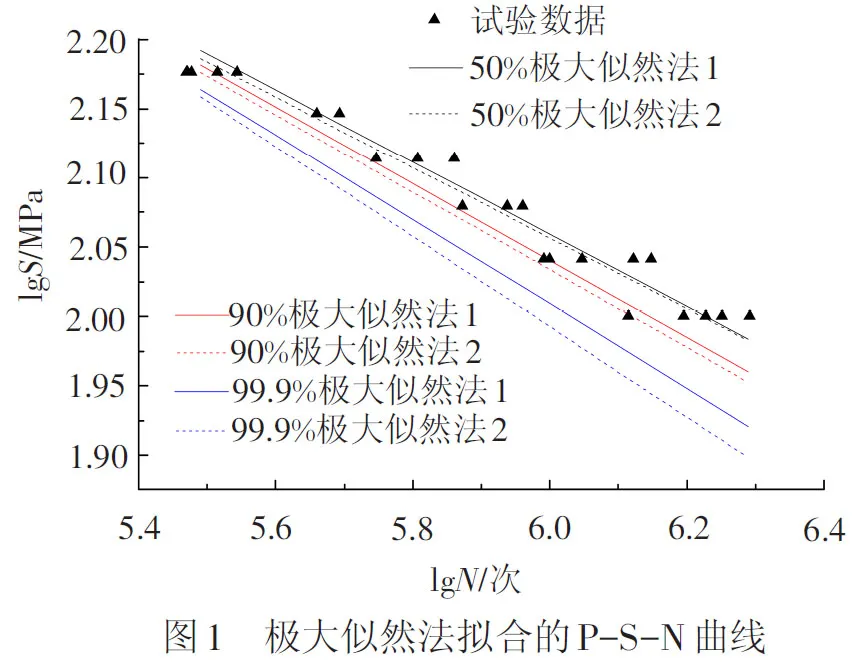
从图1拟合效果可知：

(1) 采用2种极大似然法拟合的曲线未出现存活率高的曲线上穿存活率低的曲线，符合疲劳寿命分布的客观规律，同一方法随着应力水平的降低与存活率的增大，疲劳寿命偏差逐渐增大，符合疲劳寿命的分散度随应力水平降低而增大的规律。

(2) 采用2种极大似然法拟合的中值S-N曲线随着应力水平的降低，疲劳寿命趋为一致。

(3) 极大似然法2比极大似然法1更偏于安全，是因为极大似然法2拟合的数据是经样本信息重构与寿命等效后的数据，而极大似然法1是对试验数据进行直接寿命等效，未考虑样本数量与异常样本对整体样本分布的影响，从而使得极大似然法2的寿命标准差要稍大一些。

3.2 最小二乘法拟合P-S-N曲线

根据最小二乘法直接对表1中的试验数据进行拟合的曲线称为最小二乘法1；根据2.3节的方法对表2的数据分析处理，拟合的曲线称为最小二乘法2，采用两种方法分别拟合存活率p为50%、90%、99.9%时的P-S-N曲线，见图2。

从图2拟合效果可知:

(1) 采用最小二乘法与上述极大似然法拟合的曲线整体特征基本一致。

(2) 通过对试验数据进行样本信息重构和寿命等效，在高应力区最小二乘法1在最小二乘法2的下方，但在低应力区呈相反趋势。

(3) 在存活率大的条件下，最小二乘法2比最小二乘法1要更偏于安全，是因为经样本信息重构与寿命等效后的寿命标准差要稍大一些。

3.3 对比分析

为了确定最优的拟合方法，采用上述4种方法分别拟合存活率p为50%与99.9%时的重构或等效后的试验数据，见图3。

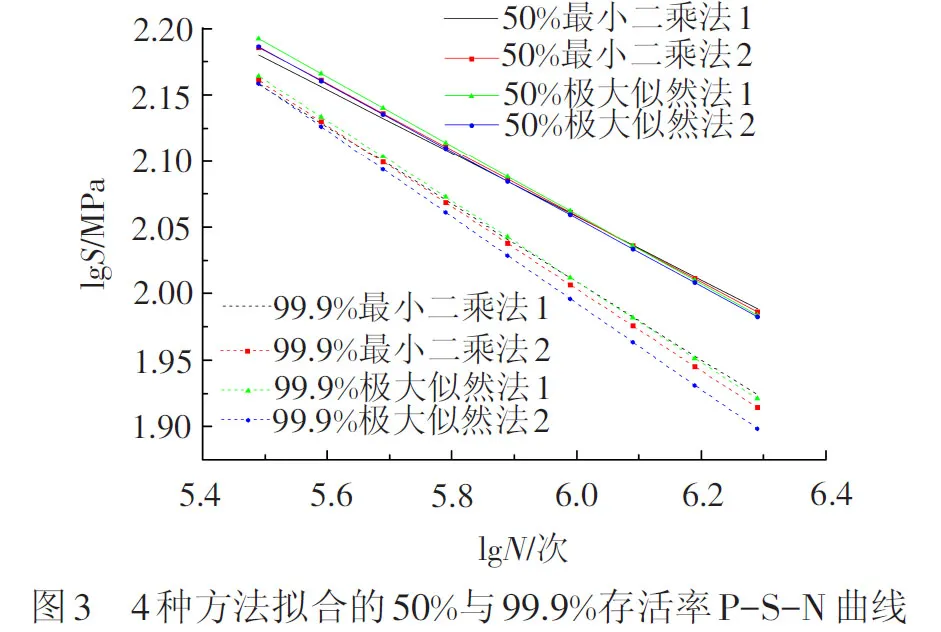
从图3拟合效果可知：

(1) 存活率为50%时，疲劳试验数据中对数寿命均值与对数应力水平自身有较好的线性关系，因此通过极大似然法或最小二乘法拟合S-N曲线基本趋于一致。

(2) 存活率为99.9%时，最小二乘法1在最上方，极大似然法2在最下方，因此极大似然法2给出了更偏于安全的拟合结果。

4 结论

(1) 本文提出了样本信息重构的方法，有效降低了个别异常样本与小子样对寿命均值与标准差的影响，提高了各应力水平下寿命均值与标准差的精度，保证了疲劳寿命等效的准确度。

(2) 本文提出了基于样本信息重构的寿命等效原理，不仅考虑了不同应力水平下样本数量对样本整体分布的影响；而且将所有应力水平下的样本疲劳寿命等效到特定的应力水平下，扩展了样本数量，修正了寿命均值与方差，最大程度逼近材料的真实疲劳寿命。

(3) 采用基于样本信息重构并符合疲劳寿命等效原理的极大似然法，基于样本信息重构的最小二乘法与传统的极大似然法，最小二乘法对试验数据进行了P-S-N曲线拟合，并通过对比分析4种方法的拟合效果，最终得出基于样本信息重构并符合疲劳寿命等效原理的极大似然法拟合的P-S-N曲线精度较高，且偏于安全。