大风环境下高速列车加速运行气动特性研究
2018-07-20刘智超梁习锋牛纪强
刘智超, 周 丹, 梁习锋, 牛纪强
(1. 中南大学 轨道交通安全教育部重点实验室, 湖南 长沙 410075; 2. 中南大学 轨道交通安全关键技术国际合作联合实验室, 湖南 长沙 410075;3. 中南大学 轨道交通列车安全保障技术国家地方联合工程研究中心, 湖南 长沙 410075; 4. 中南大学 交通运输工程学院, 湖南 长沙 410075)
高速列车具有速度高、质量轻、抗倾覆能力差等特点,相对于无风环境,大风环境下其气动特性变化更加显著[1-4]。高速列车在运行过程中不可避免的存在出站等加速运行的情况,而当存在环境风时,高速列车在加速运行过程中气动力、力矩等会发生较大变化,影响乘客乘坐舒适性,严重时可能会威胁到列车的运行安全。
为了提高列车在风环境中的运行安全性,近几十年国内外研究人员通过实车试验、模型试验和数值计算方法,对列车在横风下的空气动力学性能进行了大量研究。Baker等[5-7]对横风下高速列车的气动特性及周围流场进行了数值模拟,研究得到横风下气动载荷的频率及利用阵风模拟自然风的可行性。考虑到横风作用下的非定常特性,部分学者采用DES方法对高速列车横风下非定常气动特性进行了数值模拟[8-9]。田红旗[10-11]和毛军等[12]分别通过风洞试验和数值模拟方法得到了大风环境下高速列车阻力系数与风速、风向角及车速之间的关系表达式,并提出部分减阻措施。意大利学者通过风洞试验研究了不同地形及横风对高速列车气动性能的影响[13-14]。Cheli等[15]通过风洞试验和数值模拟相结合的方法重点研究了EMUV250高速列车在横风状态下的运行状况并得到其气动载荷系数。大部分学者主要研究了横风环境下高速列车匀速运行时气动载荷及周围流场变化,而对于高速列车匀加速过程中气动载荷及流场变化的研究则鲜有涉及。
本文采用数值计算方法,利用滑移网格技术,对横风风速为15 m/s时,高速列车分别以加速度0.5、1.0、1.5 m/s2匀加速运行过程的流场进行了仿真模拟。根据模拟结果,得到了高速列车加速过程中列车表面压力、周围流场结构、气动力及力矩的变化规律及不同加速度对高速列车气动载荷的影响。
1 数值模拟方法
1.1 数值求解方法
本文列车运行最高速度为200 km/h,横风速度为15 m/s,对应的马赫数小于0.3,在计算中空气按照不可压缩黏性流考虑[16]。采用基于有限体积法的国际主流CFD软件——Fluent求解列车周围流场;计算中通过Fluent中的UDF功能控制列车的运行速度,以实现列车的匀加速。横风下列车周围流场处于强湍流状态。计算初始时刻,首先对大风条件下列车静止在线路上进行计算,直到在整个计算区域列车初始状态下的流场结构建立起来之后,再模拟列车的加速运行过程。采用三维、非定常、不可压缩的N-S方程和Realizablek-ε湍流模型求解整个流场。压力-速度耦合的求解采用SIMPLE算法,空间压力采用标准格式离散。为获得更高的计算精度,提高计算结果的准确性,动量方程、湍流方程、湍流耗散率均采用具有二阶精度的二阶迎风离散格式。为了能通过相对较少的时间求出给定时刻的解,时间离散格式采用一阶全隐离散格式[17]。由于列车加速运行过程中车速一直在变化,经过多次试算,选择以最高运行速度200 km/h运行时的最优时间步长0.005 s作为整个加速过程的时间步长,能兼顾计算效率和计算结果的准确性。
1.2 模型与网格
为保证高速列车运行过程中气动力和力矩模拟的精确性,在计算模型中保留了列车的转向架、风挡等结构;考虑到计算能力的限制和编组长度中中间车变化规律一致等特点[12],将列车缩减为3节(头车,中间车和尾车),以车高3.7 m为特征长度H,则全长20.65H,宽0.91H,高H。图1为列车几何模型。

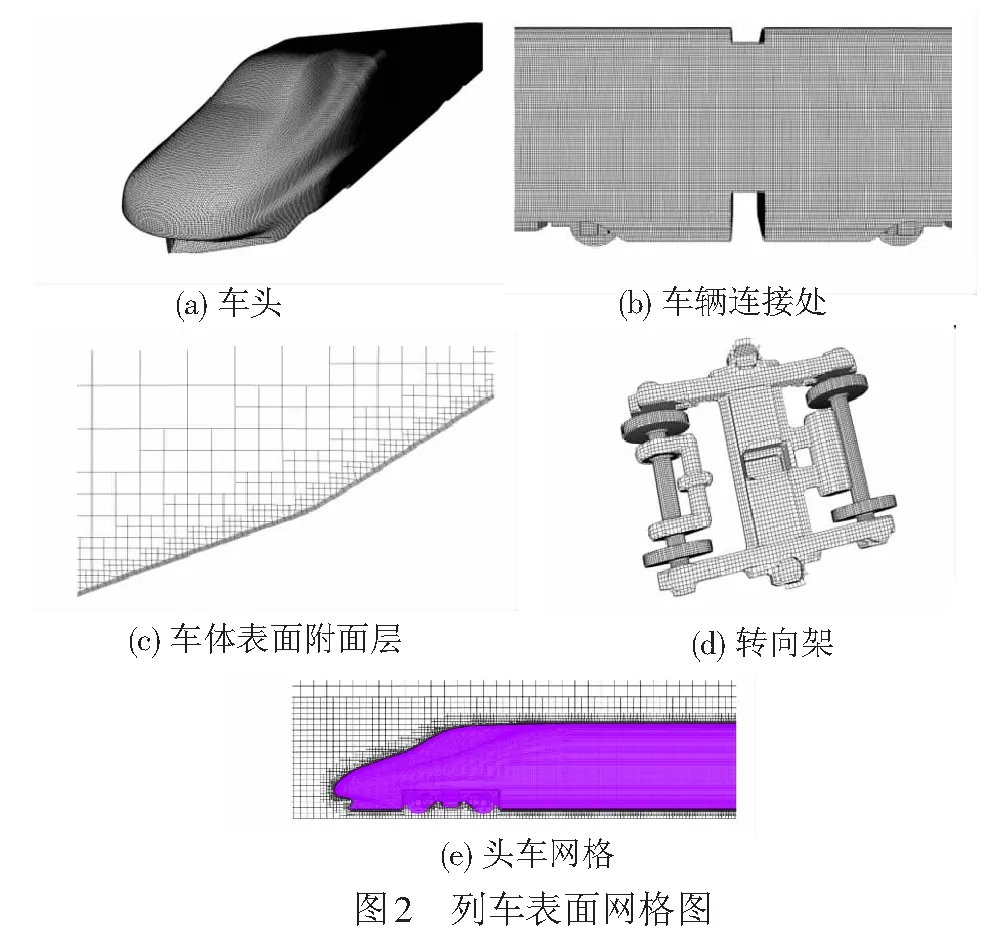
采用滑移网格技术模拟列车在横风下匀加速运行状况,流场信息通过交换面进行传递。采用开源软件Openfoam对车体周围滑移区域进行网格离散,车身表面设置10层网格来模拟附面层,使y+数值控制在30~300之间。其网格见图2。
1.3 计算域与边界条件
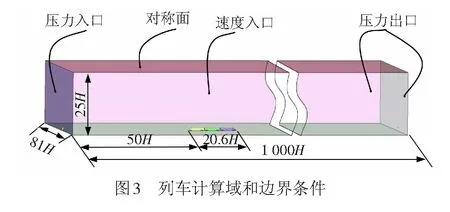
图3为列车的计算域和边界条件。整个计算域长1 000H,包括列车加速运行距离(1 m/s2加速运行距离长418H)、匀速运行距离、车尾预留距离,其中车尾距离出口端50H;宽81H,迎风侧入口距离轨道中心线26H,背风侧距离轨道中心线55H;高25H。数值模拟计算中一般将实际问题划分为有限区域进行,在区域边界上给定边界条件。列车前进方向为X轴正方向,水平面上垂直于列车前进方向为Y轴方向,垂向水平面为Z轴方向。横风方向沿Y轴,且按均匀来流给定速度大小,在横风入口为速度入口边界条件(u,v,w)in=(uf,0,0)in,横风出口为压力出口边界条件,出口静压为0 Pa。由于整个计算域近尾车和近头车的2个端面已经远离列车主流区域(50H及以上),基本不会对列车周围流场产生影响。在尾车端面设置压力入口边界,近头车端面设置压力出口边界,保证2个端面边界处基本与周围大气一致。2个区域的边界分界面设置为交换面边界条件,进行数据交换。列车所在区域的运行速度为列车运行速度。流域上下底面按光滑壁面处理,给定无滑移边界条件。
2 数值计算结果验证
2.1 气动系数计算公式
为便于研究分析,本文将列车表面压力、阻力、侧向力进行无量纲化,得到无量纲系数——列车表面压力系数Cp、阻力系数Cx、侧向力系数Cy。其分别为:
压力系数
( 1 )
阻力系数
( 2 )
侧力系数
( 3 )
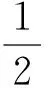
数值模拟中气动系数均方根值计算式为
( 4 )
式中:xi为各个时刻下空气动力系数;n为样本总数。
2.2 风洞试验
风洞模型试验的试验介质与真实情况相同,是研究列车气动特性应用最广泛的手段之一[16]。通过风洞试验数据和数值计算结果的对比,验证数值计算结果的准确性。风洞试验在中国空气动力研究与发展中心低速所8 m×6 m风洞中进行,其试验装置见图4。

2.3 风洞与数值计算结果对比
列车匀速运动状态下数值计算的非定常气动力系数均方根值与风洞试验得到的阻力系数和侧向力系数对比见图5。
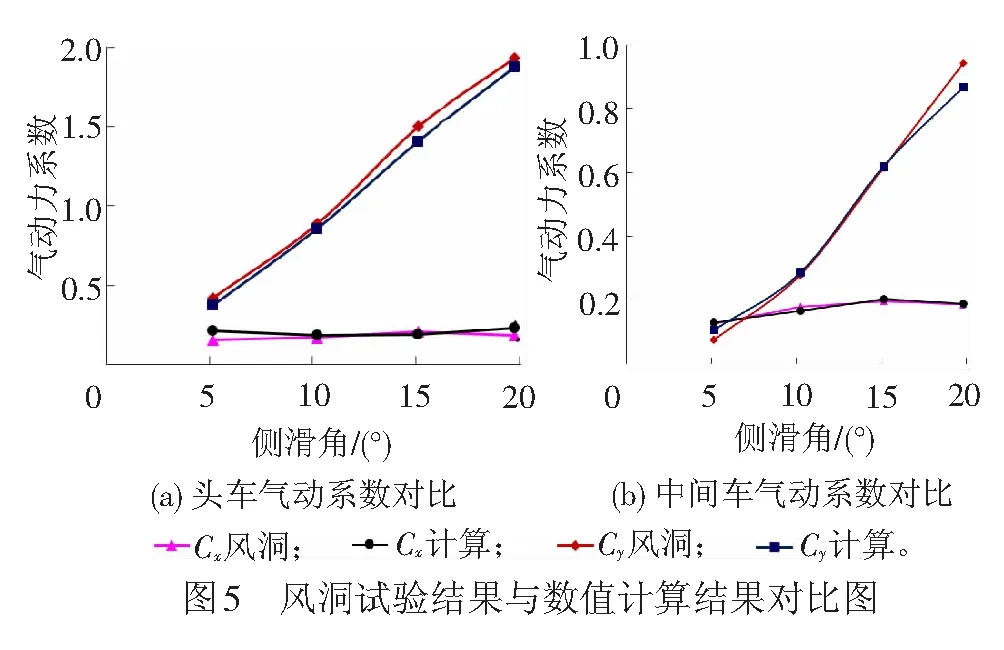
由于列车运行过程中,头车所受气动载荷的影响最大,本文以头车和中间车的阻力系数及侧向力系数进行对比分析。由图5可以看出无论是阻力系数还是侧向力系数,数值计算结果与风洞试验结果的规律基本一致,二者系数吻合较好,经计算,最大误差在10%之内,满足本次计算的要求。
3 数值计算结果分析
3.1 高速列车加速运行气动性能变化规律
高速列车在大风环境下匀加速运行时,由于环境风与列车风的耦合作用及列车运行速度的不断变化,列车表面压力、流场结构、气动载荷分布规律均不同于列车匀速运行。因而,本文对高速列车以1.5 m/s2的加速度在15 m/s横风环境中匀加速运行过程中, 0 s(列车静止)、10 s(车速54 km/h)、20 s(车速108 km/h)、30 s(车速162 km/h)、37 s(车速200 km/h)时刻下的气动性能进行对比分析。
3.1.1 表面压力
图6为大风环境下高速列车以1.5 m/s2匀加速运行过程中, 0、10、20、30、37 s时刻下的车体表面压力分布对比图。
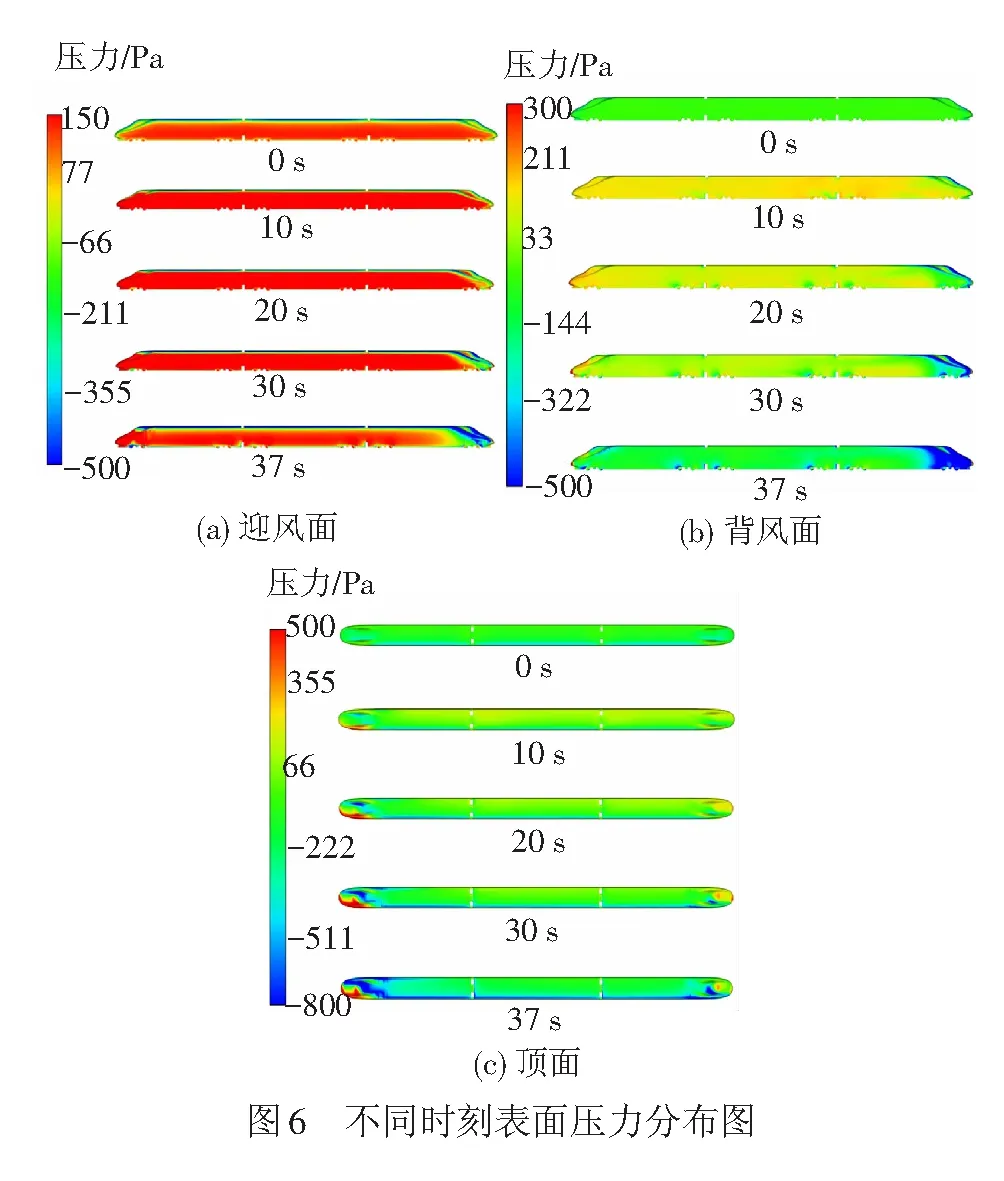
由图6可以看出:高速列车静止时,迎风面为正压,背风面为负压,且头、尾车压力呈现对称分布。列车在匀加速运行过程中,除尾部流线型区域外,列车的迎风面基本处于正压状态;列车背风面和顶面基本为负压和微正压状态;随着匀加速时间的增加(即车速的增加),在头车鼻尖偏向迎风面的区域形成的正压逐渐增大,气流在头车流线型过渡处与车体发生分离,导致此处压力逐渐减小,形成负压;尾车的鼻尖周围区域逐渐形成较小的正压,同时尾车流线型过渡处形成较大的负压并随着列车运行时间的增加,负压的绝对值迅速增加。
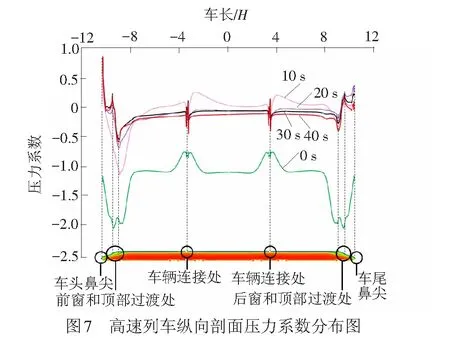
图7为高速列车匀加速运行不同时刻的纵向剖面表面压力系数分布图。从图中可以看出在高速列车匀加速运行的不同时刻,头车、尾车和车辆连接部位压力波动存在明显差异。随着列车匀加速时间的增加,鼻尖附近的正压区域逐渐增大,10 s(车速增加到与风速大小相等)时,压力波动范围最大。0 s时(列车静止,在15 m/s的横风作用下),整车的压力关于中间车的中间位置对称分布,鼻尖处为负压,且与其他时刻的压力分布差异显著。
3.1.2 流场结构
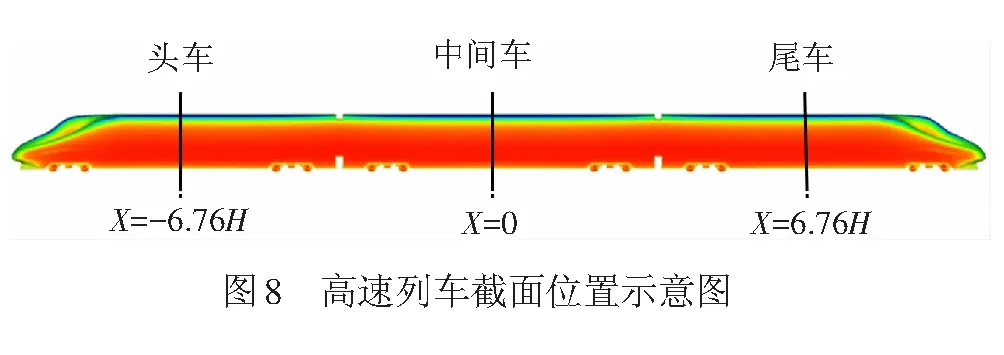
本文选取高速列车3个截面位置的流场结构进行研究,其中中间车中间位置为0处,头车选取离中心-6.76H处,尾车为6.76H处。图8为高速列车截面位置示意图,图9为匀加速不同时刻列车截面流线图。

由图9可以看出,在横风作用下,高速列车周围流场结构随匀加速运行过程不断发生改变。0 s(即高速列车静止,仅受到横风作用)时,列车背风侧车体附近形成2个近似上下对称的涡结构系。同一时刻,列车表面(X=-6.76H)形成的涡不断向列车后方运动,并最终脱离列车表面而渐渐消失。随列车运行时间的增加,列车下方的涡渐渐远离列车表面并最终与列车表面脱离,列车上方的涡逐渐向列车下方移动,得到充分发展后逐渐远离列车表面,涡强减弱,最终消失。20 s时,X=6.76H处截面可以看出,在匀加速后列车下方的涡几乎完全消失。
3.1.3 气动载荷
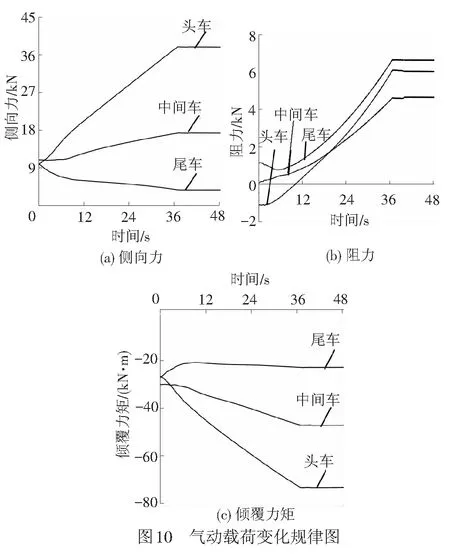
图10为在15 m/s横风作用下,高速列车在以1.5 m/s2匀加速运行过程中,侧向力、阻力和倾覆力矩的变化曲线。由图10可知,高速列车在匀加速运行过程中侧向力、阻力、倾覆力矩呈非线性增大趋势,其中头车变化最大。高速列车匀加速37 s后头车的侧向力是匀加速10 s后的2.03倍,中间车为1.46倍,尾车为0.61倍。匀加速37 s后中间车的阻力为匀加速10 s后阻力的6.96倍,尾车为6.23倍。匀加速37 s后头车的倾覆力矩是匀加速10 s后的1.74倍,中间车为1.42倍,尾车为1.11倍。
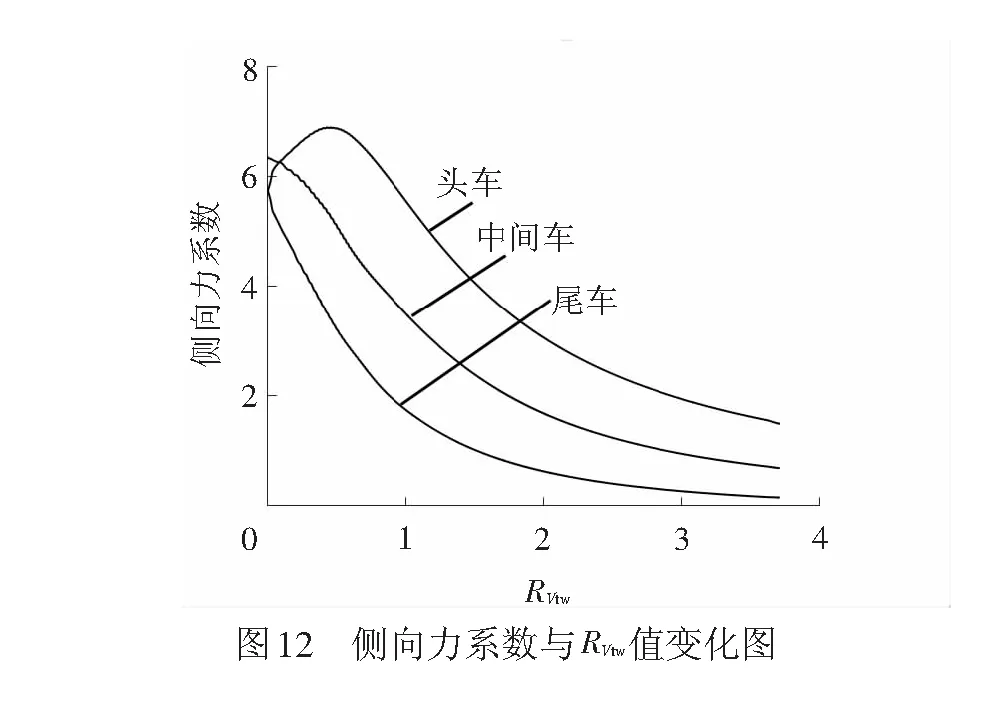
为进一步探索加速过程中气动载荷产生变化的原因,将车速和风速进行无量纲化,即横坐标为车速与风速的比值RVtw=Vt/Vw。图11、图12,分别表示阻力系数、侧向力系数与RVtw值之间的关系。
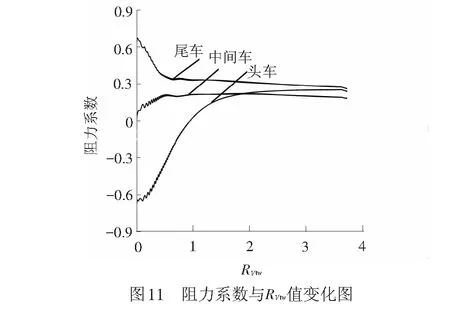
由图11可以看出,头车阻力系数随车速的增加由负转正;中间车阻力系数随车速的增加而增大;尾车阻力系数随车速的增加而减小。在匀加速过程中,各车阻力系数变化率随RVtw值的减小而减小,且在RVtw值大于3时,各车阻力系数的变化率低于0.05。
图12显示头车的侧向力系数在车速小于风速数值时,先增加后迅速减小;中间车和尾车的侧向力系数随车速的增加而减小。侧向力系数的变化率随RVtw的减小而迅速减小,且在RVtw值大于3时,各车侧向力系数的变化率低于0.6。
因此,在横风风速一定时,随着列车运行速度的增加,风速对阻力系数和侧向力系数的影响不断减小。气动力系数的变化率随RVtw值的增大而迅速减小。
3.2 加速度对列车气动性能影响分析
在横风作用下,高速列车匀加速运行过程中,气动性能不断发生变化。当采用不同加速度时,达到相同速度所需的时间不一致,其侧向力、阻力、倾覆力矩在不同时间也将产生相应的变化。由于在列车匀加速过程中头车气动载荷变化最大,本文选取不同加速度下头车的阻力、侧向力、倾覆力矩进行分析,得到不同加速度对高速列车匀加速过程中气动性能的影响。图13为高速列车在15 m/s横风作用下,分别以0.5、1.0、1.5 m/s2的加速度从静止匀加速到200 km/h过程中侧向力、阻力、倾覆力矩随时间的变化图。
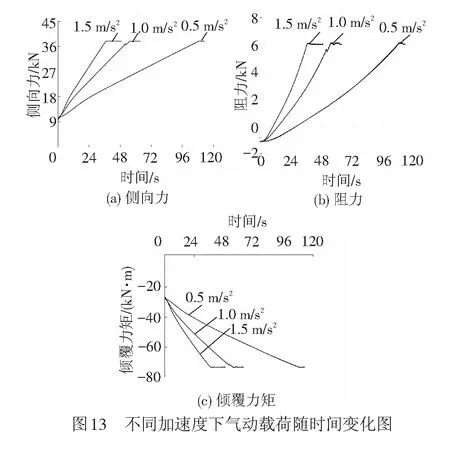
由图13可以看出,高速列车以不同加速度运行过程中,侧向力、阻力、倾覆力矩的变化规律基本相同,即随着列车匀加速时间的增加,头车的侧向力、阻力、倾覆力矩不断增大。在列车以0.5 m/s2加速度运行时,头车侧向力变化率为0.251 6 kN/s,而当加速度达到1.5 m/s2时,头车侧向力变化率达到0.755 kN/s,即在匀加速过程中,随着加速度的增加,侧向力、阻力、倾覆力矩随时间的变化率不断增大。变化率越大,短时间内高速列车气动载荷变化越大,可能严重影响列车的安全运行和乘客的舒适性。
为进一步分析高速列车运行过程中加速度对车速与气动载荷的影响,对高速列车以0.5、1.0、1.5 m/s2的加速度从静止匀加速到200 km/h过程中侧向力、阻力、倾覆力矩随车速的变化进行了研究,见图14。
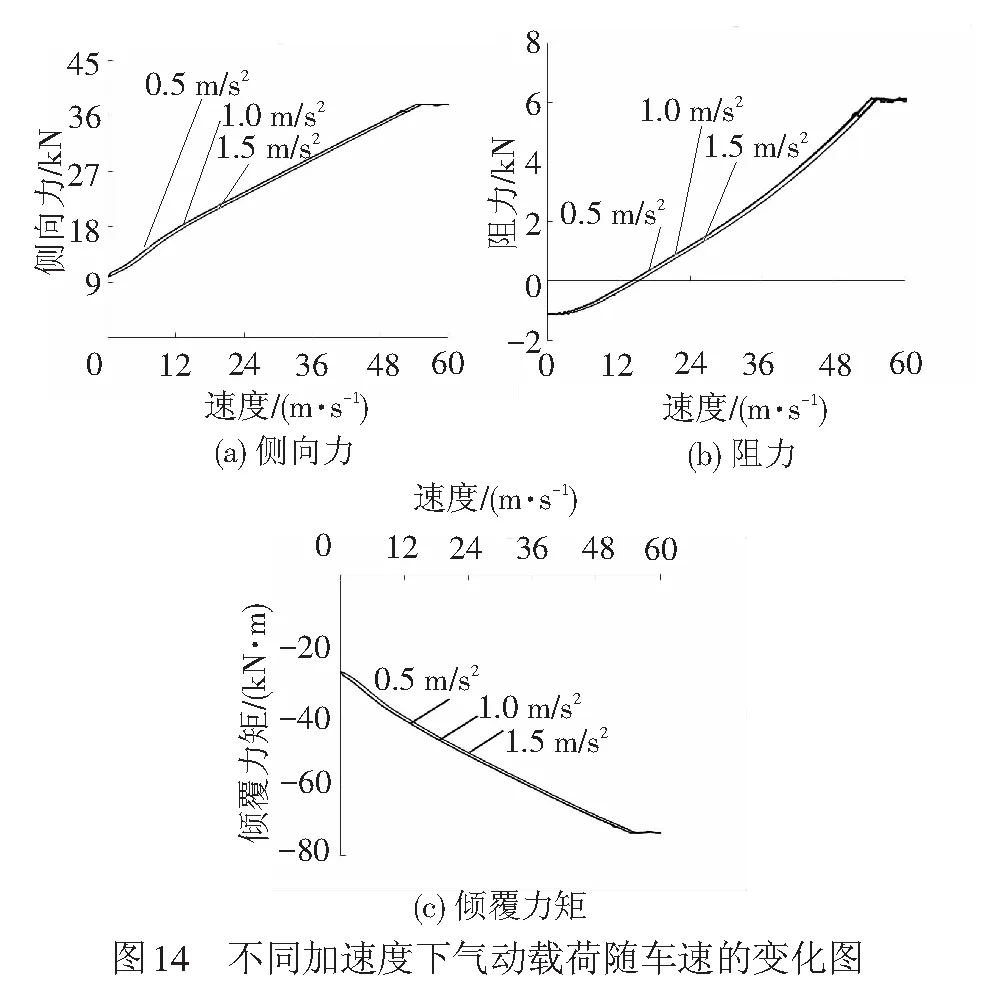
由图14可以看出,无论高速列车的加速度为多少,列车运行到相同速度时的气动载荷是一致的。高速列车运行过程中,气动载荷随车速的变化规律与气动载荷随时间的变化规律一致。
4 结论
通过对在15 m/s的大风环境下高速列车从静止匀加速到200 km/h运行过程中的压力、速度、气动载荷等进行分析,得到以下结论:
(1) 在横风的作用下,高速列车在匀加速运行过程中,迎风面(除尾部流线型部位外)基本为正压,背风面和顶面基本为负压;列车静止时鼻尖处不再为正压,且整车的压力关于中间车中间位置呈对称分布。
(2) 高速列车匀加速的不同时刻,头车、尾车和车辆连接部位压力存在明显波动,当列车运行速度大小与风速大小相等时,压力波动最剧烈。
(3) 大风环境中,高速列车静止时背风侧形成2个近似上下对称的涡系,随着匀加速时间的增加,列车下方的涡得到充分发展后逐渐远离列车表面,涡强度减弱,最终消失。
(4) 在横风风速一定时,随着列车运行速度的增加,风速对阻力系数和侧向力系数的影响不断减小。气动力系数的变化率随车速与风速比值的增大而迅速减小。当车速与风速的比值大于3时,各车阻力系数的变化率降到0.05以下,侧向力系数的变化率降到0.6以下。
(5) 当高速列车以0.5 m/s2加速度运行时,头车侧向力变化率为0.251 6 kN/s,而当加速度达到1.5 m/s2时,头车侧向力变化率达到0.755 kN/s。高速列车在以不同的加速度运行时,随着加速度的增加,侧向力、阻力、倾覆力矩的变化率不断增大,将导致短时间内高速列车气动载荷的变化增大,可能严重影响列车的安全运行和乘客的舒适性。
