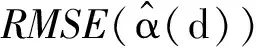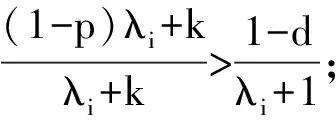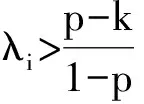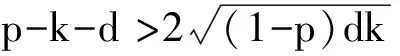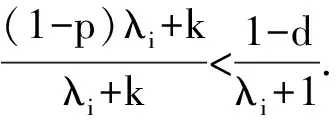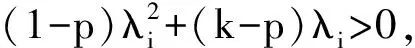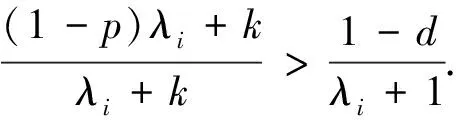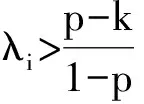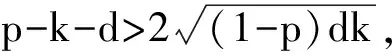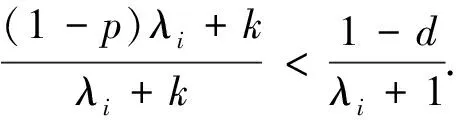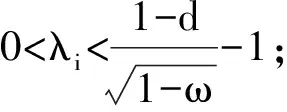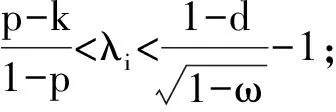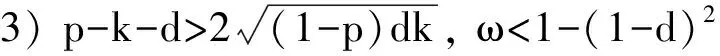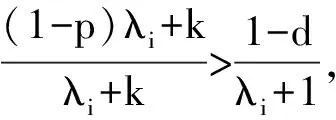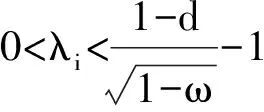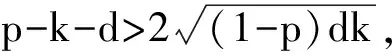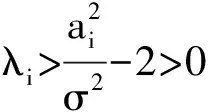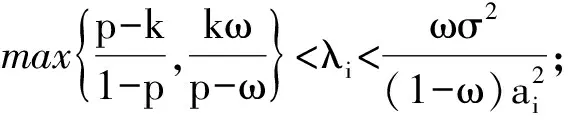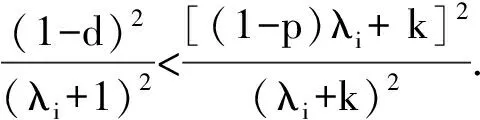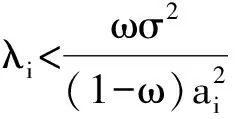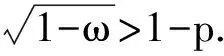平衡损失函数下几乎无偏估计的统计性质
2018-07-19王文钐赵世舜
王文钐, 赵世舜
(吉林大学 数学学院, 长春 130012)
0 引 言
考虑线性模型:
y=Xβ+ε, ε~N(0,σ2I),
(1)
其中: y是n×1的观测向量; X是秩为m的n×m矩阵; β是m×1的未知参数向量; ε是n×1的随机误差向量. 线性模型(1)的典则形式为y=Zα+ε. 设矩阵X′X特征根λ1≥λ2≥…≥λm>0的标准正交化特征向量为ρ1,ρ2,…,ρm, 记Q=(ρ1,ρ2,…,ρm)′, Z=XQ, α=Q′β, 则
Z′Z=Q′X′XQ=Λ=diag(λ1,λ2,…λm).
当矩阵X存在复共线性时, X′X的病态使得(X′X)-1的部分特征值较大, 导致参数β的估计在m维空间某些方向上严重偏离实际值. 为了克服这种病态现象, 可引入各种有偏估计, 如文献[1]的主成分估计、文献[2]的岭估计和文献[3]的Liu估计等. 为有效降低有偏估计的偏差, Kadiyala[4]提出了几乎无偏估计的概念, 并在此基础上得到了一类几乎无偏压缩估计. 由于几乎无偏估计在克服数据共线性的同时减少了估计量的偏差, 因此受到广泛关注[5-7]. 文献[6]在Liu估计的基础上提出了几乎无偏Liu估计; 文献[8]讨论了几乎无偏Liu估计的预测性质. 文献[9]在Stein岭型主成分估计的基础上, 对其进行几乎无偏化, 得到了几乎无偏Stein岭型主成分估计, 并证明其在均方误差下优于最小二乘估计. 本文在文献[9]工作的基础上, 进一步讨论几乎无偏Stein岭型主成分估计与几乎无偏Liu估计在平衡损失函数下的性质.
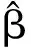
其典则形式为
其中0 其中:k>0; 0 引理1在平衡损失函数下, 几乎无偏Liu估计与几乎无偏Stein岭型主成分估计的风险差为 证明: 由于 其中: 所以 又由于 故 由于 其中: 从而 又由于 因此在平衡损失函数下, 有 证毕. (2) (1-p)λi(λi+1)+(λi+1)k>(1-d)(λi+k), 定理1当λi,ai,k,p,ω,d满足下列条件之一时, 在平衡损失函数下, 几乎无偏Liu估计优于几乎无偏Stein岭型主成分估计: (3) 从而有 结论成立. 再由1)的证明知结论成立. 从而有 结论成立. 证毕. 定理2当λi,ai,k,p,ω,d满足下列条件之一时, 在平衡损失函数下, 几乎无偏Stein岭型主成分估计优于几乎无偏Liu估计: (4) 结论成立. 从而 进而有 结论成立. 证毕.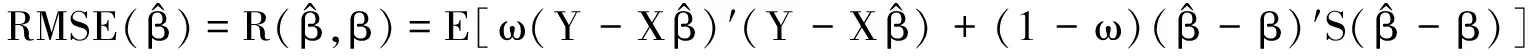
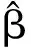

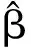

1 主要结果