模糊模范畴中的余极限

周 鑫

(1. 伊犁师范学院 数学与统计分院, 新疆 伊宁 835000; 2. 东北师范大学 数学与统计学院, 长春 130024)

模糊集[1]用于刻画客观事物的不确定性, 定义为: 设X是一个非空集合, 集合X的模糊子集可由隶属函数A:X→[0,1]刻画, 其中:X称为A的承载集, 记为K(A)=X; [0,1]称为真值集. 为了使模糊集概念能刻画更一般的事物, Goguen[2]引入了L-fuzzy子集的概念, 其真值集由比[0,1]更一般的完全分配格L替代; Rosenfeld[3]引入了模糊子群的概念, 使得模糊代数有了更深入的发展; Negoită等[4]引入了模糊模的概念; 潘福铮[5-6]介绍了模糊模范畴, 并研究了该范畴中的有限生成模糊模及正合序列等问题.

极限理论是范畴学中的重要概念之一[7], 目前, 模糊模范畴中关于极限和余极限[8]的研究已有许多结果. 例如: 赵彬[9]研究了分子格范畴中的极限问题; Gunduz等[10]定义了模糊模范畴中的正向系统及反向系统， 并讨论了正向系统上的正向极限与反向系统上的反向极限以及两个极限函子的正合性问题. 由于模糊模构成的反向系统上的反向极限函子不能保持正合序列的正合性, 因此进一步引入了反向极限的第一导出函子. 汤建钢等[11-12]利用极限理论研究了格值集合范畴的层结构性质, 并证明了集合范畴中L-fuzzy结构与层结构的同构关系; 张晓媛等[13]研究了定向空间范畴DTop的逆极限和余极限, 得到了其逆极限和余极限的一致性结果; Boroński等[14]证明了拓扑图上模糊动力系统的极限问题可实现为流形上模糊动力系统的吸引子等问题; 文献[15]讨论了L-fuzzy模范畴的极限问题. 本文在文献[10，15]的基础上, 利用范畴理论, 将模糊模范畴中的正向系统和反向系统推广到更广泛的J型图, 并给出模糊模范畴中的余极限有点式和无点式刻画. 对于文献[10]给出的模糊模范畴中余极限的存在性性质, 本文通过引入模糊模范畴中余积的结构性定理, 进一步得到了余极限的存在性、唯一性和结构性定理, 并讨论模糊模范畴中极限与余极限的关系.

1 预备知识

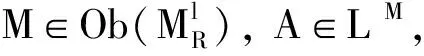
1)A(x+y)≥A(x)∧A(y);

2)A(rx)≥A(x);

3)A(0)=1, ∀r∈R,x,y∈A.

则称A是M的模糊左R-子模, 简称为模糊左R-模或模糊模. 当需要指出承载集时, 也记为AM.

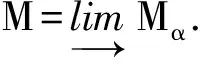
图1 F上的余锥形Fig.1 Cocone on F

图2 F的余极限Fig.2 Colimit of F

2 模糊左R-模的余极限

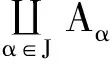
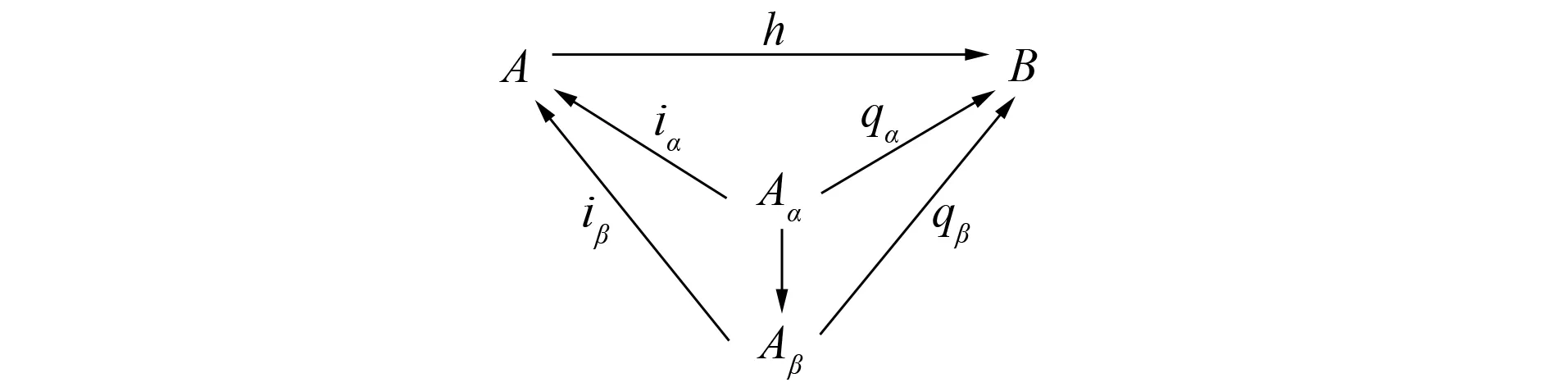
图3 F(L )的余极限Fig.3 Colimit of F(L )

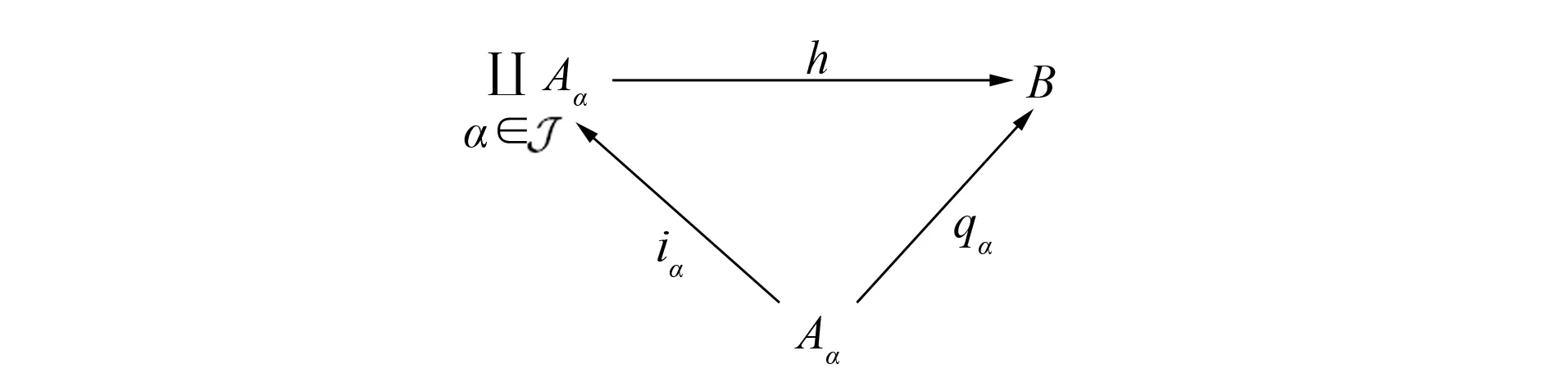
图4 {Aα}α∈J的余积Fig.4 Coproduct of {Aα}α∈J

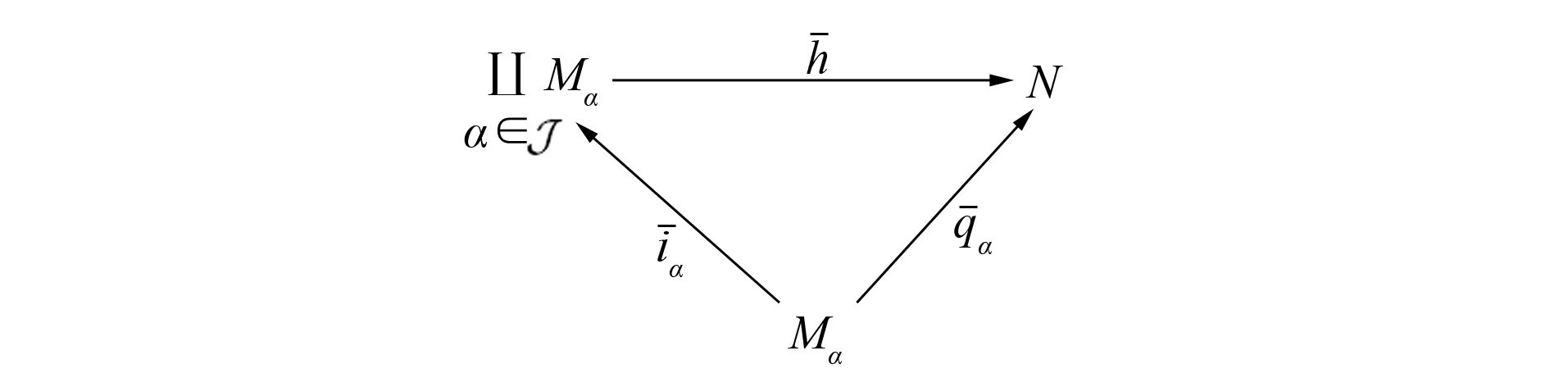
图5 {Mα}α∈J的余积Fig.5 Coproduct of {Mα}α∈J

图6 不交并为余积Fig.6 Disjoint union is coproduct

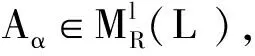
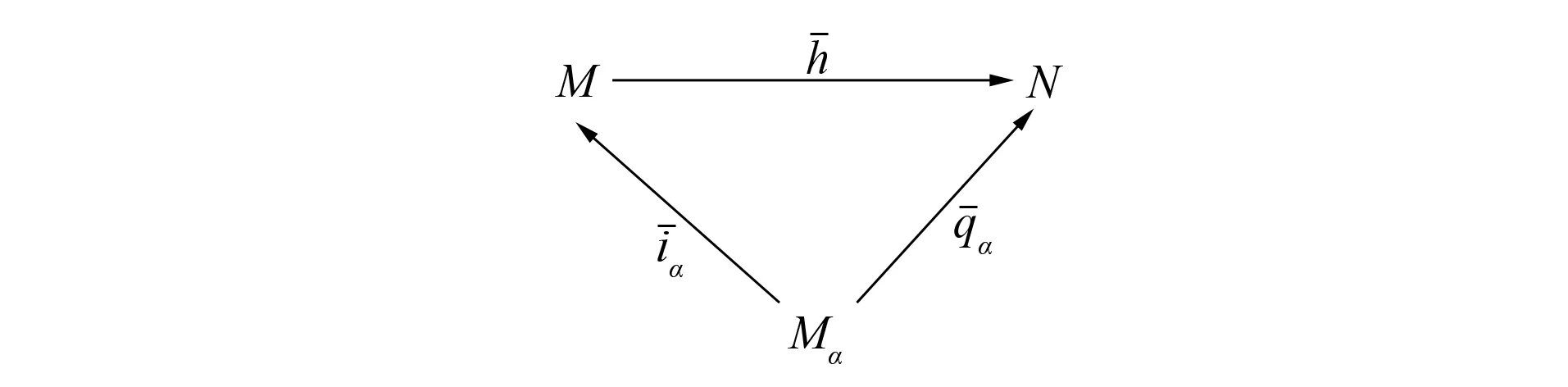
图7 {Mα}α∈J的余极限Fig.7 Colimit of {Mα}α∈J

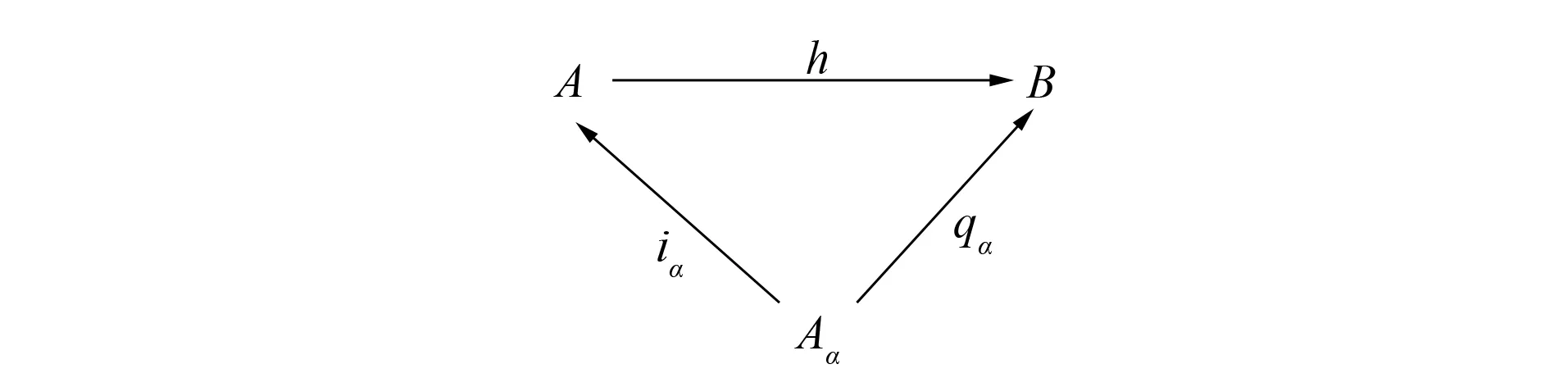
图8 {Aα}α∈J的余极限Fig.8 Colimit of {Aα}α∈J

图9 {Mα}α∈J余极限唯一Fig.9 Uniqueness of colimit of {Mα}α∈J

图10 {Aα}α∈J余极限唯一Fig.10 Uniqueness of colimit of {Aα}α∈J

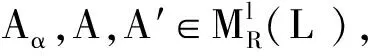
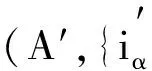
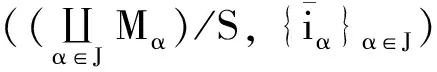
则由定理2及引理1, 得

是{Aα}α∈J的余极限.

注2余核、推出、余积及余等值子均为特殊的余极限, 故可根据定义4得到相应的概念.

3 余极限函子的伴随性

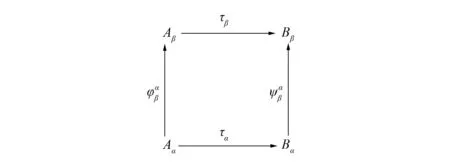
图11 自然变换τFig.11 Natural transformation τ

图12 函子τ与μ的交换Fig.12 Commutative diagram of functors τ and μ

则

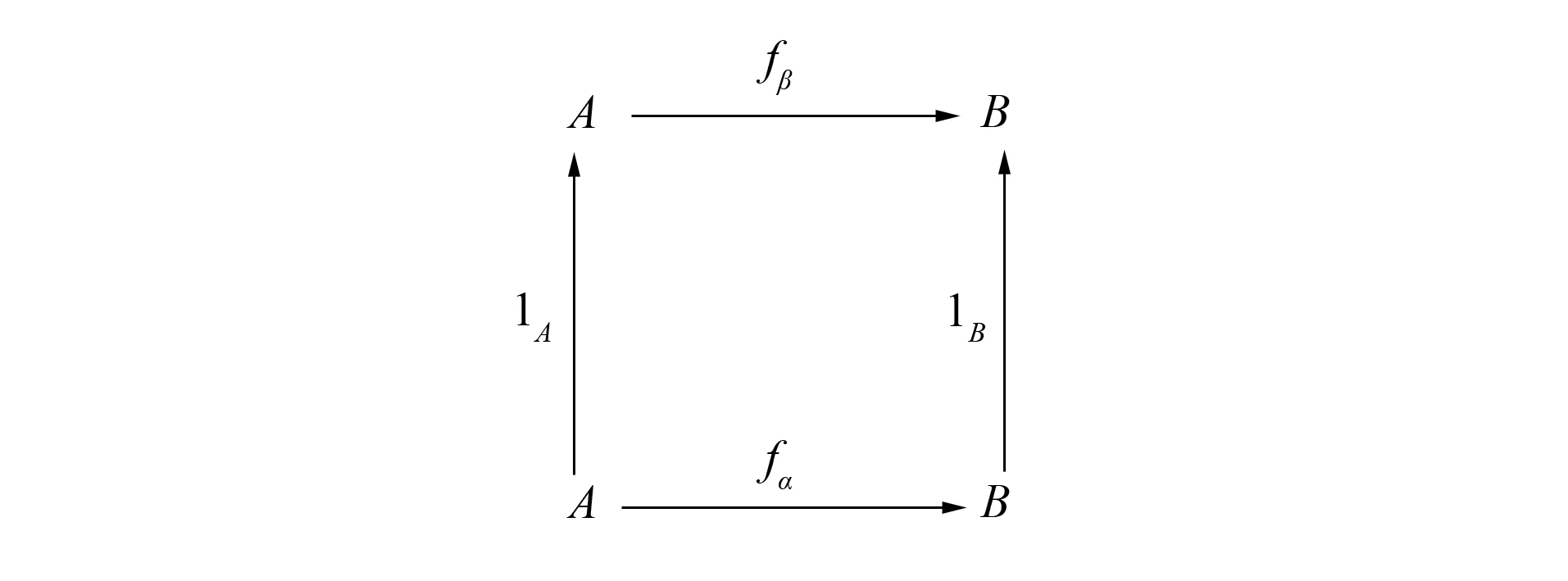
图13 自然变换|f|Fig.13 Natural transformation |f|

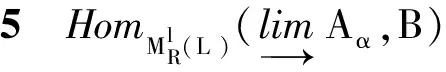
证明: 由文献[15]中定理4.4的证明及文献[19]中引理2.6.6的证明类似可得.

证明: 只证1)的第一部分, 其他类似可得.

定理7设I,J是两个小范畴, 则余极限与小范畴的顺序无关, 即

其中:α∈Ob(I );β∈Ob(J ).

证明: 由定理1和定理5可得.