左截断右删失数据下尺度参数与协变量相关时广义指数分布的估计及应用
2018-07-19王纯杰佟知真
赵 波, 王纯杰, 李 群, 佟知真
(长春工业大学 数学与统计学院, 长春 130012)
基于参数模型的统计推断是生存分析领域中的一个重要分支[1-3]. 广义指数分布[4]能在多方面弥补经典参数分布的不足, 在航空、工程、医学和生物科学等领域应用广泛, 因此双参数广义指数分布在参数模型的研究中得到广泛关注[5-9]. 关于不同数据类型的生存时间或失效时间特征的分析处理, 也是生存分析领域中的研究热点. 其中, 基于右删失数据、区间删失数据、截断数据以及双删失数据等广义指数分布参数模型的研究已有许多结果[1,10-13]. 但基于左截断右删失数据的参数模型研究文献报道较少[14-18].
本文主要基于左截断右删失数据和双参数广义指数模型, 针对尺度参数是否受到协变量因素影响建立两种模型, 采用极大似然估计法估计参数, 并利用Newton-Raphson迭代算法求解, 用随机模拟分析验证估计结果的有效性和一致性, 并将两种模型分别应用于电子变压器寿命数据集[18-19]和Channing house数据集[10]中, 给出其生存函数和风险函数.
1 左截断右删失数据下广义指数的参数估计
1.1 左截断右删失数据
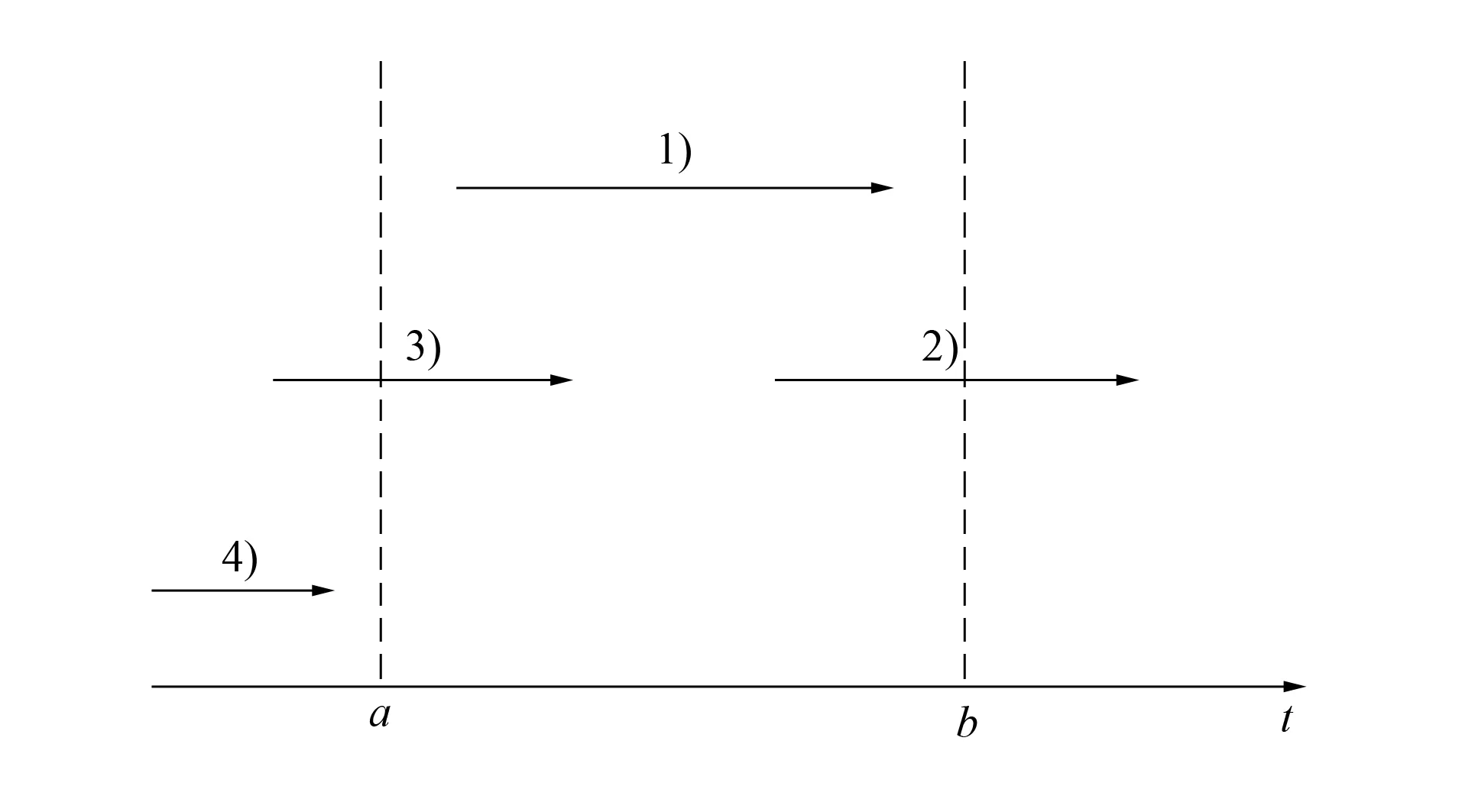
图1 左截断右删失数据实例Fig.1 Example of left truncated and right censored data
假设实验开始时间点为a, 实验结束时间点为b, 则如图1所示的左截断右删失数据包含以下4种情形: 1) 完整数据, 即兴趣事件从开始到结束都发生在区间[a,b]内; 2) 发生了右删失, 即到实验结束时兴趣事件仍在继续; 3) 发生了左截断, 即在实验开始时兴趣事件已经发生; 4) 完全左截断, 即在实验开始时兴趣事件已经结束. 实验开始时, 情形4)已经发生, 收集不到该情形下的数据, 所以本文主要考虑情形1)~3).
1.2 广义指数分布
广义指数分布是由单参数指数分布向双参数分布的一个推广, 一般记作GE(α,λ), 与单参数指数分布同为连续型分布, 其分布函数为
F(t;λ,α)=(1-exp{-λt})α,t>0,α>0,λ>0,
概率密度函数为
生存函数为
S(t;λ,α)=1-F(t;λ,α)=1-(1-exp{-λt})α,t>0,α>0,λ>0,
风险函数为
其中α和λ分别表示双参数广义指数分布的形状参数和尺度参数. 当α=1时, 风险函数可表示为h(t;λ,1)=λ, 与时间变量无关, 密度函数表示为f(t;λ,1)=λexp{-λt}, 即广义指数分布退化为指数分布.
1.3 参数估计
假设T表示观测时间变量,ti=min{yi,Ci}(i=1,2,…,n)表示第i个个体从兴趣事件发生到兴趣事件结束的时长,yi表示观测的兴趣事件从开始到结束的时长(右删失数据下的完全数据);Ci表示右删失时间. 当存在截断时,τi表示左截断时间. 设δi表示删失指示函数, 当δi=0时, 表示观测数据发生右删失, 当δi=1时, 表示观测数据未发生右删失;νi表示截断指示函数, 当νi=0时, 表示观测数据发生左截断, 当νi=1时, 表示观测数据未发生左截断. 当不考虑协变量存在时, 数据结构为D={ti,δi,νi,τi;i=1,2,…,n}; 当考虑协变量矩阵X存在时, 观测数据结构为D={ti,δi,νi,τi,Xi;i=1,2,…,n}. 取集合S,S1和S2分别表示全集、左截断数据集及S1关于S的补集(即未发生截断, 右删失数据和完整数据组成的集合), 记作S1={i:νi=0},S2={i:νi=1}.
在左截断右删失数据下, 参数的似然函数为
(1)
其中:θ表示未知参数;G(τi)表示截断部分的分布函数. 整理可得
(2)
根据左截断右删失数据下常见分布形式截断部分分布函数的取法[16-18,20], 取截断点的分布与兴趣时间一致为广义指数分布, 即G(τi)=(1-exp{-λτi})α, 所以在左截断右删失数据下, 广义指数分布的似然函数可表示为
因此, 对数似然函数为
1.3.1 广义指数参数模型 由于不考虑分布的尺度参数受协变量因素的影响, 因此可直接根据该数据类型下广义指数分布的对数似然函数, 用极大似然估计法和Newton-Raphson迭代算法极大化求解, 估计参数θ=(λ,α). 对似然函数LL(λ,α;D)分别关于参数λ和α求偏导, 并令其偏导数为0:
(5)
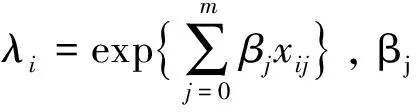
因此关于参数θ=(α,β0,β1,…,βm)的一阶导数为
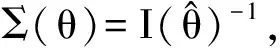
(7)
Newton-Raphson迭代算法步骤如下:
1) 给定参数迭代的初始值θ0=(λ0,α0);

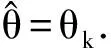
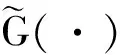
2 数值模拟
根据反解法生成广义指数分布的随机数, 即F(t;θ)=1-S(t;θ)=U,U服从均匀分布U(0,1), 反解出分布函数中的事件发生时间t. 所以当尺度参数不受协变量因素影响时,t=-λ-1log(1-U1/α); 当尺度参数受协变量因素影响时,
文献[14]中生成左截断右删失随机数的方法, 用R软件实现随机模拟. 考察不同样本量n=100,300,500, 不同删失比p=0.4,0.6和截断比q=0.3下的参数估计效果.
当尺度参数不受协变量因素影响时, 假设兴趣时间变量T服从参数为θ=(α,λ)的广义指数分布, 截断部分时间的分布与兴趣时间变量T的分布一致, 但其截断数受截断比q控制. 删失时间点分布服从参数为k的指数分布, 参数k的取值由删失比p的取值决定.
模拟ⅠT服从参数为α=1.2,λ=0.6的广义指数分布. 实验模拟在不同样本量n=100,300,500下, 根据删失截断分成两组, 一组删失比和截断比分别为0.4,0.3, 另一组删失比和截断比分别为0.6,0.3, 循环1 000次, 求出参数估计值, 并与真实参数值进行比较分析, 模拟结果列于表1.

表1 模拟Ⅰ(α=1.2, λ=0.6)的模拟结果*
*EST表示样本估计值; BIAS表示估计的样本偏差; SE表示标准误差; SEE表示标准差; RMS表示标准均方误差; CP表示置信水平为95%置信区间的覆盖概率.
当尺度参数受协变量因素影响时, 设兴趣时间变量T服从参数为θ=(α,λi=exp{β0+β1x1i})的广义指数分布, 协变量x1服从概率为0.5的二项分布, 即x1~B(n,1,0.5).
模拟Ⅱ 形状参数α=1.2, 决定尺度参数的两个回归参数为β0=0.8,β1=0.6. 实验模拟在样本量n=100,300,500、删失比和截断比分别为0.4,0.3的条件下循环模拟1 000次, 模拟结果列于表2.
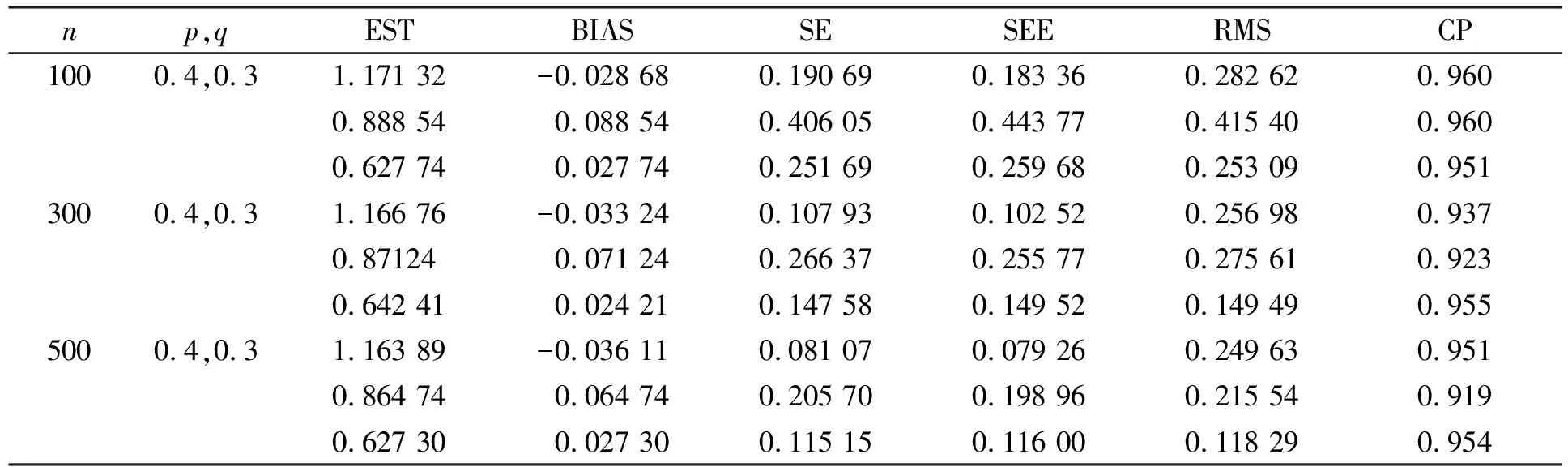
表2 模拟Ⅱ(α=1.2, β0=0.8, β1=0.6)的模拟结果*
*EST表示样本估计值; BIAS表示估计的样本偏差; SE表示标准误差; SEE表示标准差; RMS表示标准均方误差; CP表示置信水平为95%置信区间的覆盖概率.
由表1和表2可见, 估计值基本接近真实值, SE,SEE,RMS的取值较接近, 估计稳定, 且随样本量的增大, 估计的偏差和标准差均减小, 因此在该种数据类型下, 估计的结果有很好的稳定性和一致性, 表明Newton-Raphson迭代算法在极大似然估计中能精确、有效地估计模型参数.
3 实例分析
例1电子变压器寿命数据集[18-19]. 该数据集共有286个观测值, 正常失效数据39个, 发生删失的数据247个, 发生截断的数据167个, 所以其删失比和截断比分别为86.36%,58.39%. 用t表示跟踪的寿命时长,τ表示观测的截断部分时间,δ,v分别表示删失和截断的示性变量, 发生删失或者截断, 则δ或v取0, 反之取1.
考虑在左截断右删失数据下, 广义指数分布的参数模型, 可得变压器的生存(可靠性)函数为
S(t;λ,α)=1-(1-exp{-λt})α,
危险率函数为
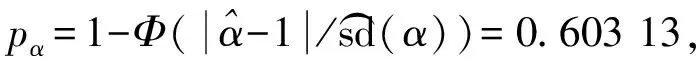

表3 变压器寿命数据分析结果
例2美国Channing house 数据集[1,10]. 该数据集, 即1964-01至1975-07美国加州帕洛阿尔托市退休中心462名老年居民的死亡时间数据集. 其中数据只有实际寿命超过实验起始点时才能观测、记录, 因此退休居民进入实验的年龄即为所需截断点. 进入年龄小于840个月(70 a)的个体组成的数据子集表示发生截断, 截断比为18.0%, 截断部分用τ表示, 示性函数v取0表示截断, 取1表示未发生截断; 存活超过实验截止时间表示删失, 删失比为61.8%, 示性函数δ取0表示删失, 取1表示未发生删失. 该数据集中有女性365名, 男性97名, 用协变量x表示,x=1表示女性,x=2表示男性.
在带有尺度参数回归时, 可得生存函数为
S(t;α,β0,β1)=1-(1-exp{-exp{β0+β1x}t})α,
风险函数为
当尺度参数不受协变量影响时, 利用广义指数参数模型, 并根据性别分组分析, 结果列于表4. 由表4可见, 男性和女性的生存函数形状参数、尺度参数较接近, 男性和女性的生存函数基本相同.

表4 当尺度参数不受协变量影响时, Channing house数据分析结果
当尺度参数受协变量影响时, 利用广义指数尺度参数回归模型将性别因素作为协变量处理, 结果列于表5. 由表5可见, 截距项β0=1.865 37, 协变量性别的回归系数β1=0.012 94, 计算协变量β1对应的p值为0.206 34, 表明性别因素对生存概率的影响不显著, 性别因素对加州帕洛阿尔托市退休中心老年居民生存概率的影响不明显.

表5 当尺度参数受协变量影响时, Channing house数据分析结果
