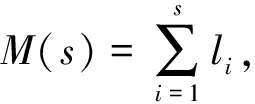图形密码中层次级联图的几种标号
2018-07-19王露露李敬文
王露露, 李敬文, 姚 兵,2
(1. 兰州交通大学 电子与信息工程学院, 兰州 730070; 2. 西北师范大学 数学与统计学院, 兰州 730070)
1 引言与预备知识
图形密码是利用人们对图形记忆优于对文本记忆的特点而设计的一种新型密码[1-2]. 用户不需要记忆冗长的字符串, 只通过识别或记住图形即可进行身份验证. 如果图形数量足够大, 则图形密码的密钥空间远远超过文本密码, 从而可以更好地抵抗暴力破解和字典攻击等. 因此, 图形密码能提供比文本密码更强的安全性.
图形密码利用拓扑图加数论等技术产生, 具有动态性强、智商高、组合方式无穷多、存储量多和运算快等优点. 文献[3-4]提出“图结构+图论”的新型密码设计思想, 是一种设计使用者方便、破译困难的图结构密码. 但图结构密码的设计需要图论提供足够多的图结构、图标号以及灵活多变的组合. 目前, 关于各类图的各种标号研究已有很多结果[5-11]. 层次级联图, 即将路一层一层的联接起来, 使得下一层路的顶点数比上一层的顶点数多2个而形成的图. 本文利用层次级联图这种特殊的图, 研究一种新型的图形密码.
定义1[5-7]如果(p,q)-图G有一个映射f:V(G)→[0,q], 使得不同顶点u,v∈V(G)均满足f(u)≠f(v), 且边标号集合定义为
f(E(G))={f(uv)=|f(u)-f(v)|:uv∈E(G)=[1,q]},
则称f为图G的一个优美标号, 图G称为优美图. 此外, 如果树T有一个完美匹配M和优美标号f, 使得树T的每条边uv∈M都满足f(u)+f(v)=n-1, 则称T为强优美树,f称为T的强优美标号.
定义2[5-7]若图G是偶图, 其顶点集合的二部划分(X,Y)满足max{f(x):x∈X} 定义3[5-7]如果(p,q)-图G有一个映射f:V(G)→[0,2q-1], 使得不同顶点u,v∈V(G)均满足f(u)≠f(v), 且边标号集合定义为 f(E(G))={f(uv)=|f(u)-f(v)|:uv∈E(G)=[1,2q-1]o}, 则称f为图G的一个奇优美标号, 图G称为奇优美图. 设当n=1时, 层次级联图的总个数为p1=5, 一层的层次级联图G1顶点的序列号分为两部分, 分别为X1={x1,x2,x3}和Y1={y1,y2}, 顶点之间的边为E(G1)={x1y1,x2y2,y2x3,y2x1}. 设当n=2时, 层次级联图的总个数为p2=11, 二层的层次级联图G2顶点的序列号分为两部分, 分别为X2=X1∪{x4,x5,x6}和Y2=Y1∪{y3,y4,y5}, 顶点之间的边为 E(G2)=E(G1)∪{x3y3,x5y5,y3x4,y4x5,y5x6,y5x3}. 设当n=3时, 层次级联图的总个数为p3=19, 三层的层次级联图G3顶点的序列号分为两部分, 分别为X3=X2∪{x7,x8,x9,x10}和Y3=Y2∪{y6,y7,y8,y9}, 顶点之间的边为 E(G3)=E(G2)∪{x6y6,x7y7,x8y8,x9y9,y6x7,y8x9,y9x10,y9x6}. 依次设当n=k时, 层次级联图的总个数为pk=(k+2)(k+1)-1,k层的层次级联图Gk顶点的序列号分为两部分, 分别为 (1) 顶点之间的边为 E(Gk)=E(Gk-1)∪{x(k+1)k/2y(k+1)k/2,…,y(k+1)k/2x(k+1)k/2+1,…,y(k+2)(k+1)/2x(k+1)k/2}. (2) 顶点的序列号如图1所示. 图1 层次级联图的顶点序列号Fig.1 Order number of vertices of hierarchical-graph 定理1层次级联图G是集有序优美图. 证明: 因为层次级联图G有p=(k+2)(k+1)-1个顶点, 故给出图G的标号函数f如下: 1)f(xi)=i-1,i=1,2,…,(p+1)/2; 2)f(yj)=p-j,j=1,2,…,(p-1)/2. 记f(X)={xi}=[0,(p-1)/2],f(Y)={yj}=[(p+1)/2,p-1], 易见fmax(X) f(X)∪f(Y)=[0,(p-1)/2]∪[(p+1)/2,p-1], 所以 f(V(G))=f(X∪Y)=[0,p-1]. 其次证所有边标号互不相同. 用数学归纳法证明: 设当n=1时, 层次级联图的总个数为p1=5, 一层的层次级联图G1顶点的序列号分为两部分, 分别为X1={x1,x2,x3}和Y1={y1,y2}, 且顶点之间的边为E(G1)={x1y1,x2y2,y2x3,y2x1}, 则G1的顶点标号和边标号分别为f(X1)={0,1,2}和f(Y1)={3,4},f(E(G1))=|f(X1)-f(Y1)|={1,2,3,4}成立; 假设当n=k时, 层次级联图的总个数为pk=(k+2)(k+1)-1,k层的层次级联图Gk顶点的序列号分为如式(1)所示的两部分, 顶点之间的边为式(2), 则Gk的顶点标号和边标号分别为f(Xk)=[0,(pk-1)/2]和f(Yk)=[(pk+1)/2,pk-1], 且f(E(Gk))=|f(Xk)-f(Yk)|=[1,pk-1]成立; 则当n=k+1时, 层次级联图的总个数为pk+1=(k+3)(k+2)-1,k+1层的层次级联图Gk+1顶点的序列号分为两部分, 分别为 (3) 顶点之间的边为 E(Gk+1)=E(Gk)∪{x(k+2)(k+1)/2y(k+2)(k+1)/2,…,y(k+2)(k+1)/2x(k+2)(k+1)/2+1,…,y(k+3)(k+2)/2x(k+2)(k+1)/2}, 则Gk+1的顶点标号和边标号分别为 且 图2 层次级联图的集有序优美标号Fig.2 Set-ordered graceful labelling of hierarchical-graph 成立. 于是证明了所有边标号互不相同, 即f(E(G))=[1,p-1], 且 fmax(X)=(p-1)/2<(p+1)/2=fmin(Y), 故层级联图G是集有序优美标号. 证毕. 图2为定理1的一个实例. 证明: 1) 构造层次级联图G的另一个标号 2) 给层次级联图G的每个顶点添加一个悬挂点, 得到层次级联图H, 在H中顶点xi的悬挂点为wi(i={1,2,…,(p+1)/2}), 顶点yj的悬挂点为zj(j={1,2,…,(p-1)/2}). 新添加的顶点标号为m(wi)=2p-1-h(xi),m(zj)=2p-1-h(yj). 当i={1,2,…,(p+1)/2},j={1,2,…,(p-1)/2}时, 显然有 h(xi)∪h(yj)=[0,2(p-1)]e,m(xi)∪m(yj)=[1,2p-1]o, 故h(V(H))=[0,2p-1]. 下面证所有边标号互不相同. 当i={1,2,…,(p+1)/2}时,h(xi)=2f(xi)=2(i-1), 此时m(wi)=2p-1-h(xi), 所以有 |m(xi)-h(xi)|=|2p-1-4(i-1)|=2p-4i+3. 当j={1,2,…,(p-1)/2}时,h(yj)=2f(yj)=2(p-j), 此时m(zj)=2p-1-h(yj), 所以 |m(yj)-h(yj)|=|2p-1-4(p-j)|=2p-4j+1. 当i={1,2,…,(p+1)/2},j={1,2,…,(p-1)/2}时, h(xi)=2f(xi)=2(i-1),h(yj)=2f(yj)=2(p-j). 用数学归纳法证明: 设当n=1时, 一层的层次级联图H1顶点的序列号分为两部分, 分别为X1={x1,x2,x3}和Y1={y1,y2}, 顶点之间的边为E(H1)={x1y1,x2y2,y2x3,y2x1}, 则H1的顶点标号和边标号分别为2f(X1)={0,2,4}和2f(Y1)={6,8},h(E(H1))=|2f(X1)-2f(Y1)|={2,4,6,8}成立; 假设当n=k时,k层的层次级联图Hk顶点的序列号分为如式(1)所示的两部分, 顶点之间的边为 据介绍,种植之前技术员为种植户提供测土服务,以土壤检测数据为依据,制定种植的底肥方案和追肥方案,底肥采用二铵或者复合肥。“今年也大面积示范不施底肥,全程追施液体肥。追肥采用配肥站提供的液体配方肥。液体配肥站采用工厂生产好的高浓缩的大量元素水溶肥、中量元素水溶肥、微量元素水溶肥为原料,根据不同作物的不同生产阶段的养分需求,应合作社和农户的要求,现场配置成液体配方肥,配好的配方肥直接进入田间使用。” E(Hk)=E(Hk-1)∪{x(k+1)k/2y(k+1)k/2,…,y(k+1)k/2x(k+1)k/2+1,…,y(k+2)(k+1)/2x(k+1)k/2}, 则Hk的顶点标号和边标号分别为2f(Xk)=[0,(pk-1)]和2f(Yk)=[(pk+1),2(pk-1)],h(E(Hk))=|2f(Xk)-2f(Yk)|=[2,2(pk-1)]成立; 当n=k+1时,k+1层的层次级联图Hk+1顶点的序列号分为如式(3)所示的两部分, 顶点之间的边为 E(Hk+1)=E(Hk)∪{x(k+2)(k+1)/2y(k+2)(k+1)/2,…,y(k+3)(k+2)/2x(k+2)(k+1)/2}, 则Hk+1的顶点标号和边标号分别为 且 成立. 于是h(E(H))=[1,2p-1]. 又因为H有一个完美匹配 M={ximi|i=1,2,…,(p+1)/2}∪{yjzj|j=1,2,…,(p-1)/2}, 从而可知H是强优美标号. 证毕. 图3为定理2的一个实例. 图3 层次级联图H强优美标号的形成过程Fig.3 Formation process of strongly graceful labelling of hierarchical-graph H 结论成立, 证毕. 图4为定理3的一个实例. 定理4给层次级联图G的每个顶点任意加叶子点得到图K, 则图K具有奇优美标号. 图4 层次级联图G的性质Fig.4 Properties of hierarchical-graph G 证明: 设图G有q=p-1条边, 令s=(p+1)/2,t=(p-1)/2, 集有序奇优美标号函数为g. 定义V(X)={xi:g(xi)=2f(xi),xi∈V(G)}是偶数,V(Y)={yj:g(yj)=2f(yj)-1,yj∈V(G)}是奇数;V(G)=V(X)∪V(Y), 其中:V(X)={xi:i∈[1,s]};V(Y)={yj:j∈[1,t]},s+t=|G|. 根据集有序奇优美标号的定义可知,g(xi) |V(K)|=|V(G)|+M(s)+M(t),E(K)=E(G)+M(s)+M(t). 定义图K的标号函数为k, 有以下3种情形: 1)k(xi)=g(xi),i∈[1,s];k(yj)=g(yj)+2(M(s)+M(t)),j∈[1,t]. 2)k(x1x1,1)=1,k(x1,1)=k(x1)+k(x1x1,1)=1, 因此k(x1)=0. 特殊边标号为k(x1x1,j)=2j-1,j∈[1,l1]. 特殊点标号为k(x1,j)=k(x1)+k(x1x1,j)=2j-1,j∈[1,l1]. 一般边标号定义为 一般点标号定义为k(xi,j)=k(xi)+k(xixi,j),j∈[1,li],i∈[2,s]. 3)k(ytyt,1)=2(M(s)+M(t))-1,k(yty1)=k(yt)-k(ytyt,1),k(ytyt,l)=k(ytyt,1)-2(l-1)=2(M(s)+M(t))-2l+1,l∈[1,k1]. 边标号为 k(yi,j)=k(yi)-k(yiyi,j),j∈[1,ki],i∈[2,t]. 下面证明图K的标号函数k是奇优美标号. 易见k(xi)(i∈[1,s])是偶数;k(yj)(j∈[1,t])是奇数;k(xi,j)(j∈[1,li],i∈[1,s])是奇数;k(yl,r)(r∈[1,kl],l∈[1,t])是偶数. 显然k(xi,j)≠k(yl,r). 注意到k(xi) 所以 k(xs,ls)=k(us)+2M(s)-1 k(yt,1)=k(x1)-2(M(s)+M(t))+1=g(yt)+1>g(xs)=h(xs). 因此对任意的x,y∈V(K),k(x)≠k(y). 设图K的边标号函数k(E(K))满足 {k(xy):xy∈E(K)E(G)}=[1,2(M(s)+M(t))-1]o, {k(xy):xy∈E(G)⊆E(K)}=[1+2(M(s)+M(t)), 2q-1+2(M(s)+M(t))]o, 则 k(E(K))=[1,2q-1+2(M(s)+M(t))]o=[1,2|E(k)|-1]o. 证毕. 图5为定理4的一个实例. 图5 层次级联图K奇优美标号的形成过程Fig.5 Formation process of odd-graceful labelling of hierarchical-graph K 综上, 本文提出了一种图作为新型图形密码的图结构, 并证明了层次级联图的相关标号, 表明层次级联图具有集有序优美标号、强优美标号、奇优美标号以及一些顶点所具有的性质.
2 主要结果