高等几何思想方法在初等几何中的应用

吴华玥

高等几何作为高师院校数学与应用数学专业学生必修的基础课程，其对初等几何的理解和教学起到指导性的作用.［1-3］通过对高等几何的学习使我们找到高等几何与初等几何的联系，并能领悟到高等几何在初等几何中的应用，从而更加深入地了解高等几何与初等几何的内在联系，可以从另一高度来看待初等几何的内容，使我们对初等几何中一些定理的生成有了新的理解，有利于更好地教学.由于高等几何包含射影几何、仿射几何与欧式几何，而欧式几何是射影几何与仿射几何的特例，因此本文将从射影几何和仿射几何两部分来探讨高等几何思想方法在初等几何中的应用.

1 仿射几何思想方法在初等几何中的应用

仿射几何作为高等几何的重要组成部分，是研究高等几何在初等几何中应用的桥梁，一些初等几何问题常常需要通过仿射几何的性质来研究.通过对仿射几何的研究，本文将总结一些仿射几何在初等几何中的应用，下面将从仿射变换和仿射坐标系两方面来讨论仿射几何思想方法在初等几何中的应用.

1.1 仿射变换的应用

变换的思想是一类很重要的数学思想，而仿射几何所研究的几何恰恰是通过仿射变换的不变性质和仿射不变的量以及图形经过变换后的形状和位置之间的关系来实现的.仿射变换具有同素性、结合性，且仿射变换保持共线三点的简比不变.利用仿射变换的性质，可以将一般图形经过某种特殊的仿射变换变换成特殊图形，如：将任意三角形变换成正三角形，将任意四边形变换成正方形或长方形，将任意椭圆变换成圆等，根据具体的仿射不变性或仿射不变量来解题，从而将一个复杂的初等几何问题简单化.

例1 ΔABC，点D为BC边上的中点，连结AD，在AD上任取一点P，连结BP，CP，延长BP，CP分别交AC，AB于E，F，求证EF//BC.

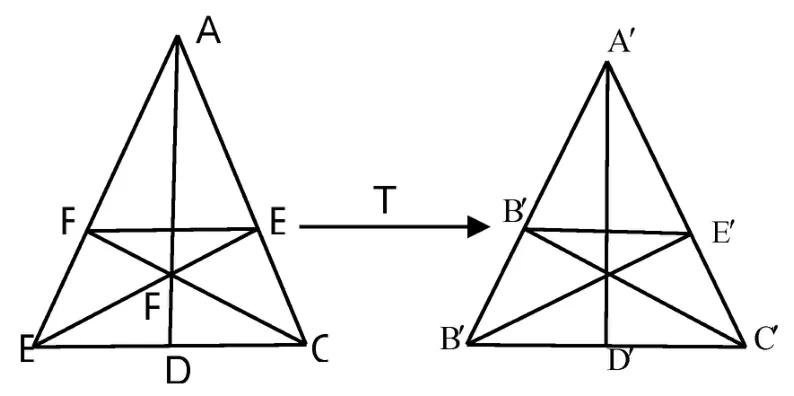
图1 三角形变换成正三角形

证明 如图1所示，将ΔABC经一仿射变换T后对应正 ΔA′B′C′，由仿射性质知，点D对应D′，点P对应P′，点E对应E′，点F对应F′，且A′D′为正 ΔA′B′C′的中线.因为 ΔA′B′C′是正三角形，所以A′D′还是B′C′边上的高，又B′，P′，E′与C′，P′，F′关于A′D′对称，且E′，F′到B′C′的距离相等，于是E′F′//B′C′，因为平行性为仿射不变性，故在ΔABC中EF//BC.

上面通过仿射变换将任意一个三角形变成正三角形，通过运用高等几何的方法来解决初等几何问题，能让我们从另一角度解决初等几何问题，从而使解题思路更加清晰，解题步骤更加简便，可见高等几何的思想方法对初等几何的指导性作用.

仿射变换不仅对简单的三角形适用，对椭圆等复杂图形仍然适用.

例2 现有一椭圆的外切三角形为ΔA′B′C′，三个切点A′1,B′1,C′1分别与对应顶点A′,B′,C′连线，求证：三线交于一点.

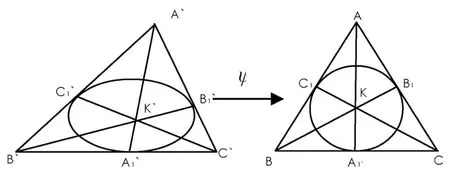
图2 三角形的内切椭圆变换成内切圆

证明 如图2所示，将ΔA′B′C′经一仿射变换ψ后变为正 ΔABC，于是 ΔA′B′C′的内切椭圆经仿射变换ψ后变为ΔABC的内切圆，则有A对应A′，B对应B′，C对应C′，因为ΔABC与ΔA′B′C′存在唯一一个仿射变换ψ，且仿射变换保持结合性，ΔABC的内切圆各切点为A1,B1,C1，所以有A1对应A′1，B1对应B′1，C1对应C′1，又因为A1A，B1B，C1C交点为K，故A′1A′，B′1B′，C′1C′交点为K′.

例3 平行四边形ABCD，点E，F分别是AB，BC边上的点，有EF//AC.求证：SΔAED=SΔCDF.

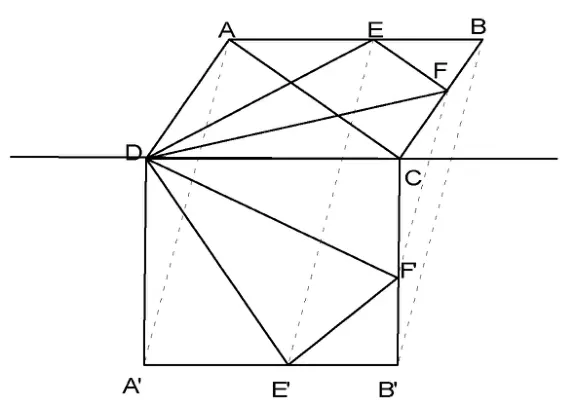
图3 平行四边形变换成正方形

证明 平行四边形ABCD经仿射变换后，变成正方形A′B′CD，则有E对应E′，F对应F′，如图3所示.

在正方形A′B′CD中，由E′F′//A′C，则因为A′B′=B′C，所以B′E′=B′F′，于是有A′E′=CF′，因为，所以ΔA′E′D≅ ΔCDF′，又因为两个多边形面积之比是仿射不变量，所以，故SΔAED=SΔCDF.

1.2 仿射坐标系的应用

与笛卡尔坐标系相比，仿射坐标系的建立具有任意性，可以根据具体的情况建立适当的仿射坐标系.因此对于一些初等几何问题可以利用建立仿射坐标系的方法，将几何问题用代数方法进行解决，使解题思路更加简洁，计算过程更加方便.

例4 在ΔABC的BC边上取D,E两点，将BC三等分，连结AD,AE，取AC中点F，连结BF，求BG:GH:HF.

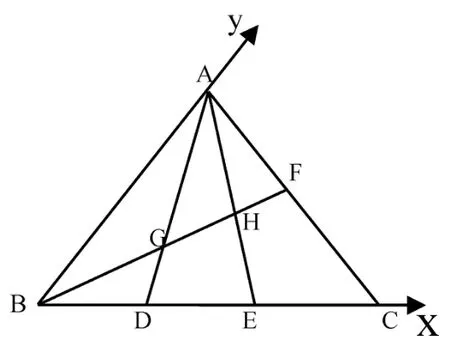
图4 三角形建立仿射坐标系

解 如图4，以B点为原点建立仿射坐标系，取B(0,0)，A(0,1)，D(1,0)，E(2,0)，C(3,0)，因为F为AC中点，则.从而得到直线BF方程为，直线AD方程为y=-x+1，直线AE方程为，从而知BF与AD交点，BF与AE交点，由定比分点公式有，从而，即.同理可得，故BG:GH:HF=5:3:2.

2 射影几何思想方法在初等几何中的应用

射影几何是高等几何中非常重要的一部分，仿射几何事实上属于射影几何的一个特例，所以射影几何的思想方法在初等几何的应用相比仿射几何的思想方法在初等几何中的应用更加广泛些.在射影几何中有许多定理与方法在初等几何中都有相应的应用，比如：Desargues定理、交比和调和比、配极原则、对偶原理等，本文将从Desargues定理以及交比和调和比这两个基本理论入手，结合具体的初等几何问题，讨论射影几何思想方法在初等几何中的应用.

2.1 Desargues定理的应用

Desargues定理是射影几何中的一个基础定理，在射影几何中许多定理以它为根据.利用De⁃sargues定理及其逆定理，可以证明初等几何中关于点线结合的命题如：三点共线问题，并使证明过程更加简便.

定理1 如果两个三点形对应顶点的连线交于一点，则对应边的交点在一条直线上.

例5 三边形的垂心，重心，外心三点共线.

已知三边形的垂心，重心，外心分别为H，I，K，且BC,AC的中点分别为P，Q，求证：点H，I，K三点共线.

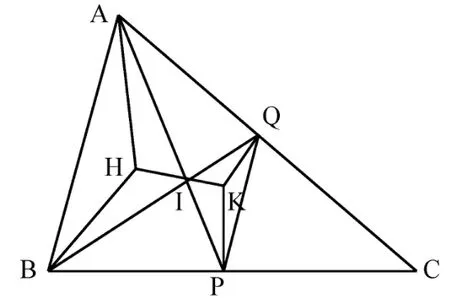
图5 三点形

证明 如图5所示，考虑三点形ABH与KPQ，由中位线性质，其所对应的AB与PQ，AH与KP，BH与KQ平行，则AB与PQ，AH与KP，BH与KQ分别交于D∞、E∞、F∞.由于D∞、E∞、F∞三点共线，所以由Des⁃argues逆定理知AP,BQ,HK交于一点，又AP,BQ交于一点I，故H，I，K三点共线.

2.2 交比和调和比的应用

与仿射几何相同的是射影几何也存在射影不变性质和射影不变量，而交比则是最基本的射影不变量，调和比则是交比的一种特殊情形，即在共线四点的交比中当交比值为-1时，则该交比值-1叫作调和比.运用交比和调和比的一些定理可以使初等几何中一些复杂的证明题变得简单化.［4］

定理2 一线段的中点就该线段两端所定的第四调和点为无穷远点；反过来，成调和共轭的四点中，如果有一点为无穷远点，则与其配偶的那一点必为以另一点偶为端点的线段的中点.

在初等几何中证明两条线段相等或者证明两个角度相等都是比较常见的初等几何证明问题，而采用有关交比和调和比的一些定理能直接解决一些复杂的平分线段或者平分角度的问题.

例6 已知四边形ABCD，AD与CB交于M，AB与CD交于N，AC与MN交于P，BD//MN，求证：MP=PN.

证明 由于在射影几何中平行则相交于无穷远点，如图6所示.设BD⋂MN=H∞，在完全四点形ABCD中，由定理3可知(MN， )PH∞=-1，故P为MN的中点，即MP=PN.

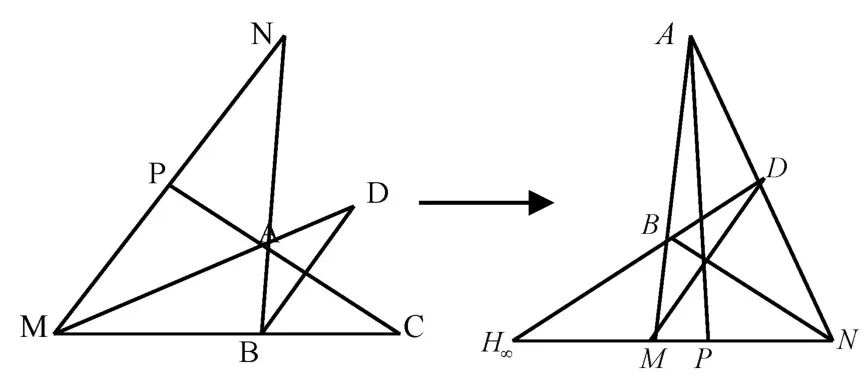
图6 变换前后的四边形

2.3 射影几何的有关定理在初等几何作图中的应用

在射影几何中，二次曲线的极与极线是其重要内容之一，有关于圆的切线在初等几何作图中也是必不可缺的.［5-7］本文将利用在射影平面中非常重要的极与极线的相关理论来解决初等几何中有关圆的切线作图问题，例如利用二次曲线的极与极线快速且准确地画出圆的切线.

例7 过圆外一点P作其切线.

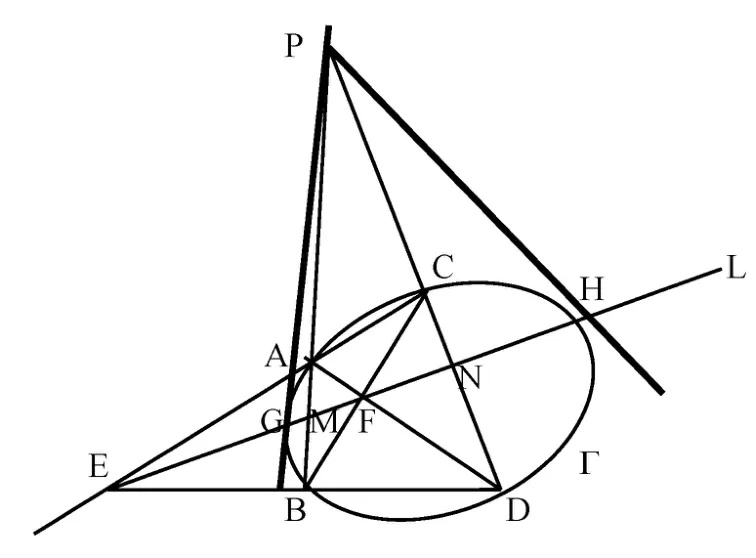
图7 二次曲线

解 在射影平面上要想作其切线，首先画出已知二次曲线Γ外一点P的极线L，如图7所示.

具体作图步骤如下：①过点P任意作两条直线，分别与二次曲线Γ交于点A,B,C,D；②AC与BD交于E，AD与BC交于F；③连结EF则为所求极线L.

证明EF与AB交点为M，EF与CD交点为N，对于完全四点形ABCD，通过每一对角点有一组调和线束，考虑调和线束E(CDPF)，用AB去截得 (CD,PM)=-1，用CD去截得(CD,PN)=-1.因为PM与二次曲线Γ交于A,B两点，所以M为P的共轭点，同理N为P的共轭点，从而MN为P的极线，即EF为P的极线.

因为P在二次曲线Γ外，极线L与二次曲线Γ交于G,H，而点G,H在极线L上，所以与点P共轭，由配极原则P一定在G的极线上，但G在二次曲线Γ上，所以它的极线就是二次曲线Γ在点G处的切线，即点P在二次曲线Γ过G点的切线上，则PG是圆的切线.同理可得PH也是切线.

3 结论

对初等几何而言，高等几何具有鲜明的指导性和应用性特征，将高等几何的原理以及方法与初等几何方法结合起来使用，值得我们进一步研究.对于将来要成为教师的我们而言，不仅仅要会用初等几何的知识解决初等几何问题，更加需要结合高等几何内容对初等几何知识有更深入的了解，不仅知其然，还要知其所以然，从更高的角度去理解和把握初等几何的实质，为初等几何的教学工作打下坚实的基础.