基于灰色马氏链模型的国内游客量预测

张水利，王玉琼，屈 聪

由于国家经济高速发展，人们的生活水平显著提高，近几年国内游客量逐年增加，对我国旅游业的发展有着重大影响.马氏链具备“无后效性”，即要确定过程将来的状态，知道它此时情况就够了，与过去所处的状态无关［1］.灰色预测模型能解决历史数据少、序列的完整性和可靠性低的问题，能将无规律的原始数据进行生成得到规律性较强的生成序列，运算简便，易于检验［2］.陈杏莉，廖文杰［3］利用灰色马尔可夫预测模型对入境旅游人数进行了研究，结果表明利用灰色马氏链模型进行预测，精度更高.为了预测国内未来几年的游客量，本文以2006-2016年的国内游客量为原始数据，建立了灰色马氏链模型，对2017-2019的国内游客量进行了预测.

1 马氏链模型

1.1 马氏链的定义

定义1［1］随机过程{Xn,n=0,1,2,…}

称为Markov链，若它只取有限或可列个值（若不另外说明，以非负整数集{ }0,1,2,… 来表示），并且对任意的n≥0，及任意状态i,j,i0,i1,…,in-1,有 P{Xn+1=j|Xn=i,…,X1=i1,X0=i0}=P{Xn+1=j|Xn=i}，式中，Xn=i表示过程在时刻n处于状态i，称{ }0,1,2,… 为该过程的状态空间，记为S.

定义2［1］称条件概率 P{Xn+1=j|Xn=i}为Markov链{Xn,n=0,1,2,…}的一步转移概率，简称转移概率，记为 pij，它表示处于状态i的过程下一步转移到状态 j的概率.

一步转移概率矩阵为 P=(pij)=

定理1［1］（C-K方程）对一切 n,m＞0,i,j∈S，有

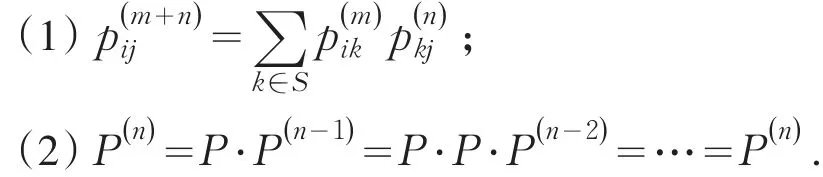
1.2 马氏性检验

将原始数据划分为n个状态，为了便于区分，用fij表示状态从i转移到j的一步频数转移矩阵，有，其中

给定置信度α，根据数据表可查出的值，若，则说明原始数列满足马氏性.

2 GM（1，1）预测模型

2.1 GM（1，1）建模步骤

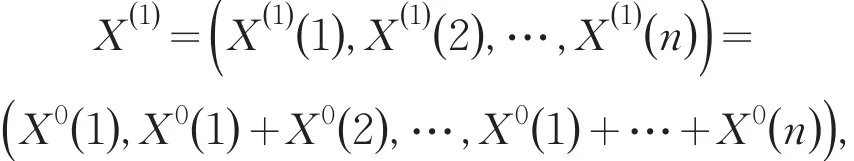
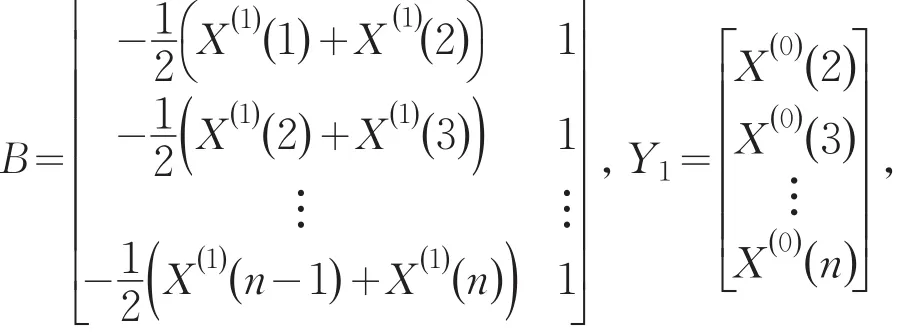
求解得到灰色预测公式［3-4］为

2.2 数据检验

把2006-2016年国内游客量数据作为原始数据，即x={1394,1610,1712,1902,2103,2641,2957,3262,3611,4000,4440}；

计算数列的级比为：

2.3 GM（1，1）模型的检验

根据MATLAB编程得到：灰色预测模型方程中a=-0.1166,u=1.3292×103，且104，则灰色预测方程为关联度检验e=0.9996，均方差比c=0.0845，小误差概率p=1，精度等级均达到1级，可见对原数据进行灰色预测的效果较好.

3 灰色马氏性模型

3.1 划分状态

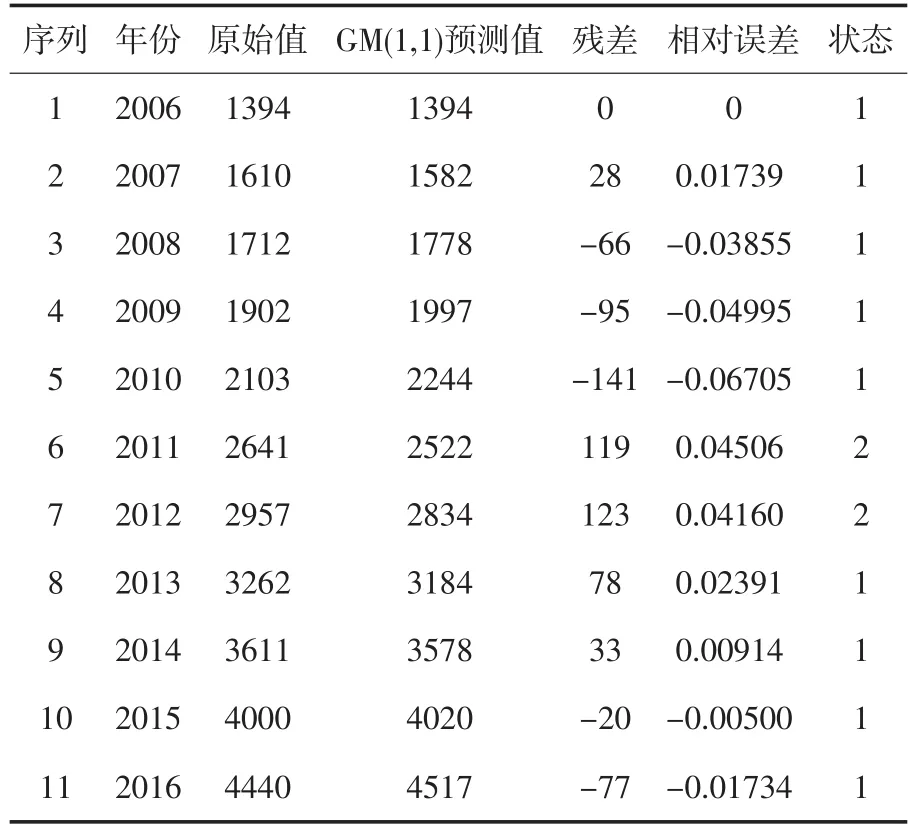
表1 GM（1，1）预测值，残差及状态划分

3.2 检验马氏性

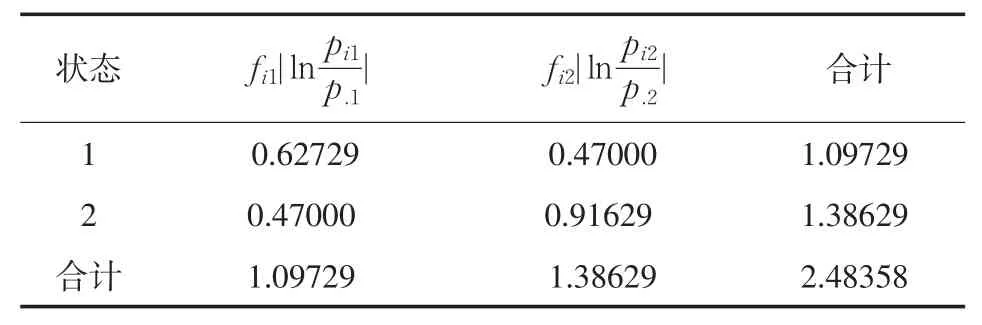
表2 卡方统计量计算

χ2=2×2.48358=4.96716，给定的置信度α=0.05，查表可知由于χ2=4.96716＞χ2(1=3.841)，所以原始数据序列具有马氏性.

3.3 计算预测值

结合状态区间范围和灰色预测值［5-6］，确定灰色马氏链模型的预测值，用M(k+1)表示，则每一个区间的计算得到的预测结果为状态1：

根据GM（1，1）模型及灰色马氏链模型对2017-2019年进行预测，并计算相对误差，结果如表3所示.

从表3可以看出，GM（1，1）模型的相对误差绝对值的平均值为3.1499%，灰色马氏链模型相对误差绝对值的平均值为2.187%，与GM（1，1）模型相比，预测精度提高了0.9629%.因此利用灰色马氏链模型进行预测时，效果更好.

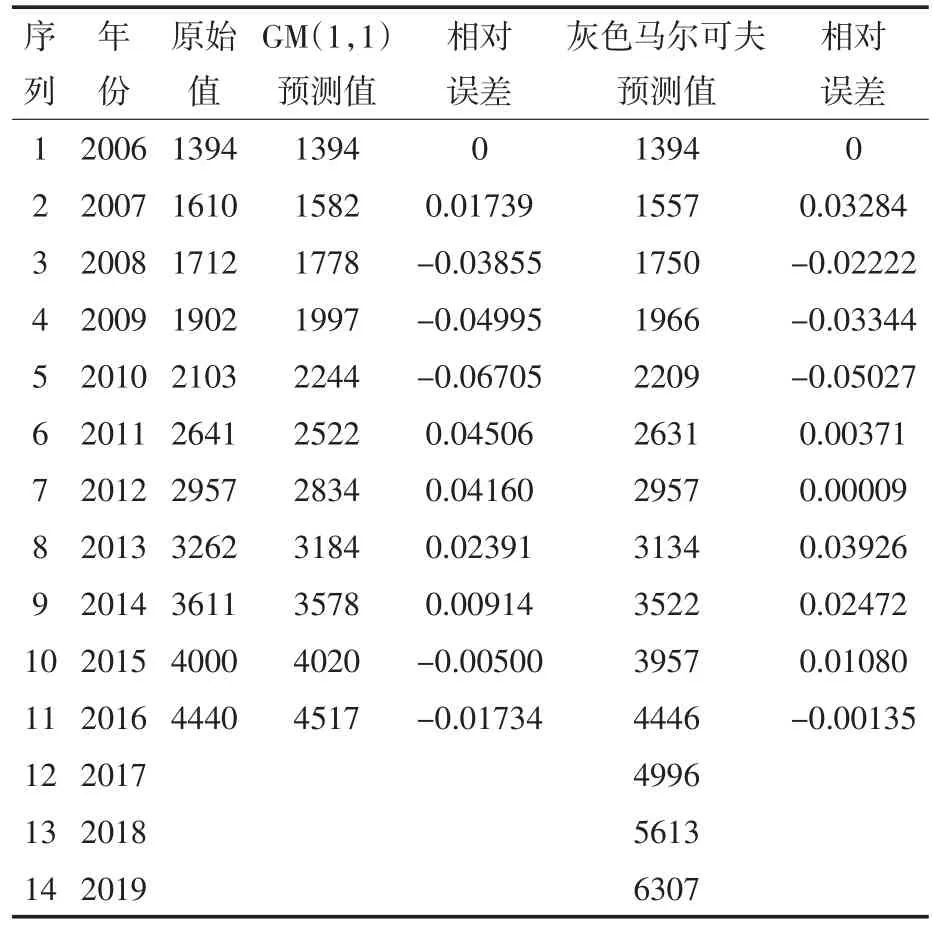
表3 灰色马尔可夫预测值及相对误差

4 结论

与GM（1，1）模型相比，灰色马氏链模型的预测精度更高，因此利用灰色马氏链模型对2017-2019年我国游客数量进行了预测，国内游客人数分别为4996万人，5613万人，6307万人.结果表明：我国游客仍将持续增长.可见我国未来旅游业发展前景会越来越好，旅游业的发展也将成为未来服务行业的重点，能够带动我国经济可持续发展.