两变量设计洪水估计的不确定性及其对水库防洪安全的影响

尹家波，郭生练，吴旭树，刘章君，熊　丰

（武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉　430072）

1　研究背景

洪水作为一种多变量随机水文事件，通常需要多个特征量才能完整描述。为了考虑各个特征量之间的内在相关性，Copula函数被引入多变量洪水频率分析中［1］。对于多变量水文频率分析计算，边缘分布和联合分布函数的确定都依赖于水文序列的样本容量，而如果样本容量太小，就会导致所估计的函数参数存在不确定性，从而使联合设计值估计产生很大的不确定性［2］。如何定量评价联合设计值估计的不确定性尤为重要。

近年来，国内研究重点主要集中在单变量估计的不确定性上。例如：鲁帆等［3］通过贝叶斯MCMC方法估计边缘分布函数参数及设计值的后验分布，并据此进行极值洪水的频率分析；胡义明等［4］利用Bootstrap方法，研究了样本抽样不确定性对水文设计值的影响，并分析了该方法在不同参数估计方法间的有效性；冯平等［5］依据贝叶斯理论将先验信息和样本信息有机结合，采用Gibbs-MCMC算法对P-Ⅲ型频率分布曲线参数的不确定性进行估计，并对比分析了非一致性序列修正前后的不确定性区间。尽管上述文献能够较好地描述单变量水文频率分析方法的不确定性，但是对多变量设计洪水的不确定性研究在国内则尚未发现［2］。国外已经开展多变量水文频率分析不确定性的研究，但仍处于起步阶段，如何对边缘分布和Copula函数的不确定性进行耦合是研究的难点。Serinaldi［6］通过Monte Carlo随机模拟方法，提出了描述两变量水文设计值估计不确定性的ALGO系列算法；Dung等［7］基于Bootstrap技术，将重现期等值线上的联合设计值进行随机模拟，并通过模拟设计值的分布规律分析了两变量设计值的不确定性。但是上述方法未能充分考虑水文事件发生的内在规律，忽略了重现期等值线上不同联合设计值的发生概率，使两变量设计值估计产生了较大的任意性和不确定性，而且无法定量评价该不确定性。同时，上述研究主要集中于如何估计联合设计值，事实上坝前最高水位才是影响水库安全的最重要因素［8-9］，国内外学者将设计洪水联合估计值引入水库防洪安全设计中，但却没有考虑联合设计值估计不确定性对水库调洪结果造成的影响。

本文基于Copula函数和Parametric Bootstrap方法，考虑两变量设计值的最可能组合模式，建立可描述两变量设计洪水估计不确定性的C-PBU（Copula-based Parametric Bootstrap Uncertainty）模型，同时提出定量评价两变量不确定性的度量指标，最后通过偏不利典型和相似特征典型两种洪水过程选取模式，对比分析联合设计值估计不确定性对水库最高调洪水位的影响。

2　Copula函数和联合重现期

Copula函数可以将多个具有不同形式边缘分布的随机变量联结起来构造联合分布。令洪峰Q的概率分布为FQ(q)，洪量W的概率分布为FW(w)。依据Sklar定理，Q和W的联合分布函数可以用Cop⁃ula函数C表示成f(q，w)=c(u，v)［10］，其中u=FQ(q)，v=FW(w)。

f(q，w)相应的联合概率密度函数可表示为［11-13］：

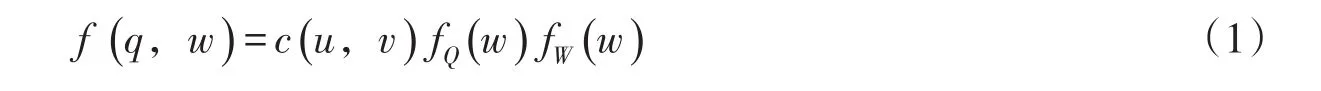
Volpi等［13］对联合重现期进行过定义和讨论，对于联合重现期的选择应当由研究对象的工程特性来确定，一般采用OR重现期作为水库的防洪标准，其定义如下［12-14］：

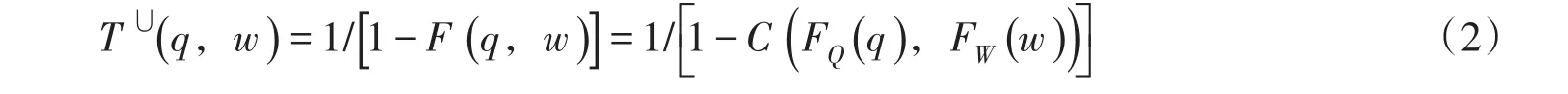
式中：T⋃(q，w)即为（Q，W）的联合重现期，以年为单位。

3　基于Copula函数和Parametric Bootstrap方法的C-PBU模型

3.1最可能组合法的数学描述Serinaldi［6］提出ALGO-C算法描述两变量设计值估计的不确定性，Dung等［7］借鉴该算法采用参数型Bootstrap方法研究了Mekong流域联合设计值估计的不确定性。但上述方法未考虑重现期等值线上不同联合设计值的发生概率，不仅增加了计算的复杂性，还会额外增加设计值估计的任意性和不确定性。事实上，重现期等值线上虽然有无数组联合设计值满足防洪标准，但是并非所有的组合模式都符合水文事件发生的内在规律［10-13］。在工程设计中，人们通过对实际发生洪水的内在特性规律分析，通常关心洪水事件的最可能组合模式［12］。因此，为了避免联合设计值选取的任意性及盲目性，本文从洪水发生可能性最大的角度，采用洪峰Q与洪量W最可能发生的组合模式作为联合设计值。

设计洪水峰量最可能组合模式是指（Q，W）在满足防洪标准的条件下，f(q，w)取最大值时的两变量联合设计值。通过构建以下联合方程求解该问题：

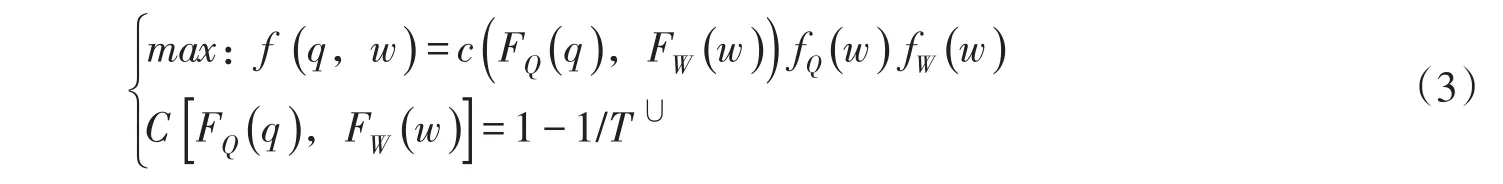
边缘分布函数及联合函数在Q及W的定义域内是连续的，故在联合重现期约束下的f(q，w)存在最大值。本文采用拉格朗日乘子法求解该问题，构造拉格朗日函数如下：

分别对q、w和λ求偏导数，并令其为0，得到下式：

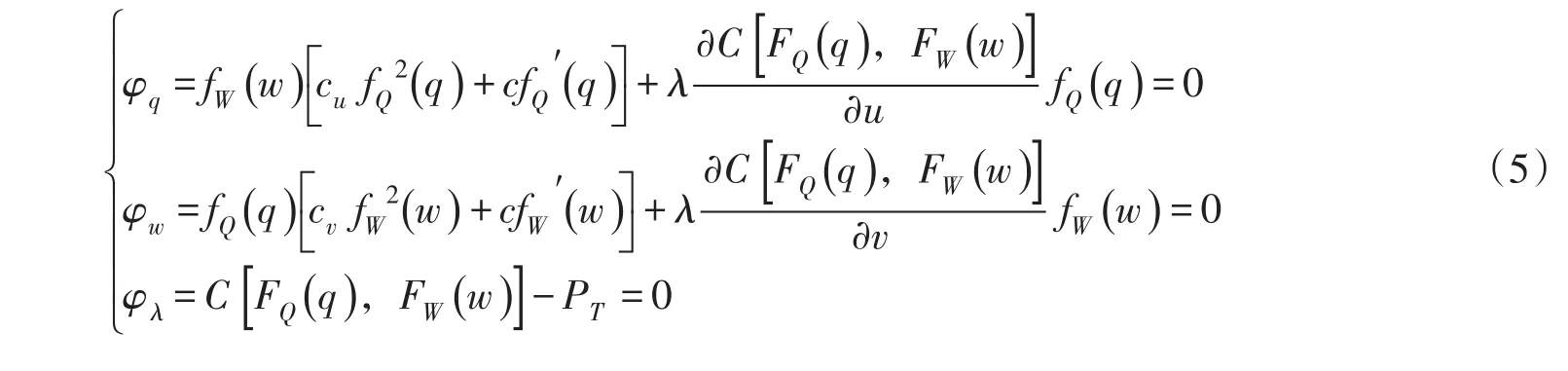
式（5）可通过数值解法求解，如二分法、牛顿迭代法等。

3.2C-PBU模型现有研究证明，Copula函数类型选取不当会对模拟序列设计值估计带来显著的不确定性［6-7］。本文为了减小该项不确定性，通过AIC统计量最小准则［13-14］对模拟的新样本序列的联合分布函数进行优选。由于Archimedean族Copula函数在水文领域中应用广泛，而且适用于描述正相关或负相关的水文变量，故本文仅考虑该族函数。为了描述两变量设计值估计的抽样不确定性，考虑两变量设计值估计的最可能组合模式，建立了C-PBU模型，主要步骤如下：

（1）根据实测样本系列估计洪峰Q和洪量W的边缘分布及Copula函数参数，建立两变量联合分布函数F(q，w，)可得到W关于Q的条件分布函数：

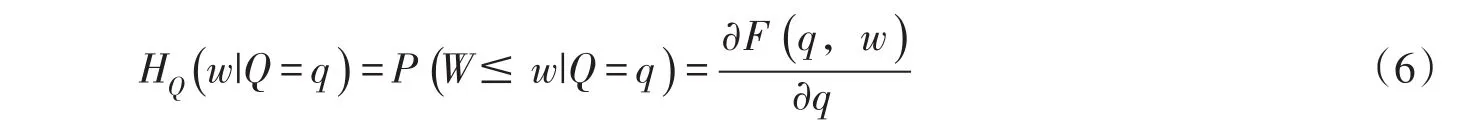
（2）设置Parametric Bootstrap需要模拟的样本容量n，产生n组服从［0，1］均匀分布的两个独立的随机数[r1i，r2i]，i=1，2，…，n；令r1i为洪峰qi发生的累积概率得到洪峰模拟值qi。

（3）令r2i表征洪峰qi发生时洪量wi的条件概率分布函数值，即r2=HQ(wi|Q=qi)，从而可依据计算得到wi。

（4）设置Parametric Bootstrap模拟次数为B，重复步骤（2）—（3）B次，即可得到B组样本容量为n的新序列(qij，wij)，其中i=1，…，n，j=1，…，B。

（5）对于模拟的B组新样本序列，通过线性矩法（L-moment）估计边缘分布函数的参数。

（6）对于模拟的B组新样本序列，分别通过Gumbel-Hougaard（G-H）、Clayton和Frank Copula函数构建联合分布，采用Kendall秩相关性系数法［7］估计参数值，选取AIC值最小的Copula函数作为联结函数，于是得到B个最优的联合分布函数Fj（q，w）。

（7）对于步骤（6）得到的每一个联合分布函数Fj（q，w），给定某一联合重现期T∪，考虑两变量设计洪水的最可能组合模式，即通过求解式（5）得到重现期等值线上的最可能设计值（qTj，wTj）。

（8）对于给定的联合重现期T∪，对B组最可能联合设计值，采用最大密度区域（Highest density re⁃gions，HDR）方法［15］得到对应于某一给定的置信水平α的(1-α)置信区域。HDR是一种非参数估计方法，根据点据的空间信息进行分析，从而求出包含(1-α)空间点集的最小区域。置信区域越大，则表示不确定性越大；反之，置信区域越小，则设计值估计的不确定性越小。

3.3不确定性度量指标现有方法［6-7，10］均未能对两变量估计的不确定性进行定量评价，为此本文提出采用横向平均偏移幅度（DQ）、纵向平均偏移幅度（DW）、置信区域面积（S）和平均欧氏距离（d）作为两变量估计不确定性的度量指标。DQ（和DW）分别用于度量洪峰（和洪量）与实测样本系列推求的设计值在一维空间的估计偏差；S和d用于度量模拟设计值点据与实测样本系列设计值的空间距离；4个度量指标越小，则表征不确定性越小。通过窗格舍取法计算置信区域的面积，其他指标的计算公式如下：

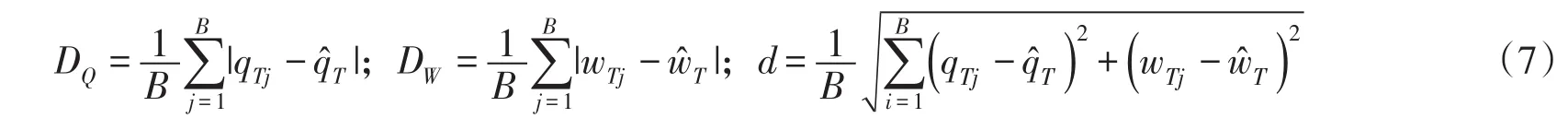
4　考虑洪水过程随机性推求设计洪水过程线

设计洪水过程线是水库防洪调度的基本依据，通常只选取一场或几场典型洪水过程进行放大，我国规范推荐选取峰高量大、主峰靠后的典型洪水过程，本文称之为偏不利典型洪水。Requena等［8］为了考虑洪水过程的随机性，根据洪水峰量设计值与M年实测洪水过程特征量的相似性来选择相应的典型过程，本文称为相似典型洪水，将该方法与C-PBU模型结合，具体如下：

在联合重现期T∪下，对于C-PBU模型步骤（7）得到的B组最可能联合设计值（qTj，wTj），首先计算qTj和wTj的比值统计最大、最小峰量比max rTj和min rTj。采用下式对模拟系列的峰量比进行归一化处理，产生（0，1）之间的峰量比系列RTj：

从M场实测洪水中选取偏差绝对值最小(min{SSTjk})的实测洪水过程，作为模拟值的相似特征典型洪水，该方法考虑了流域洪水的特点和多样性。

选取了偏不利或相似典型洪水过程后，均采用变倍比放大方法［16］来获得设计洪水过程线：

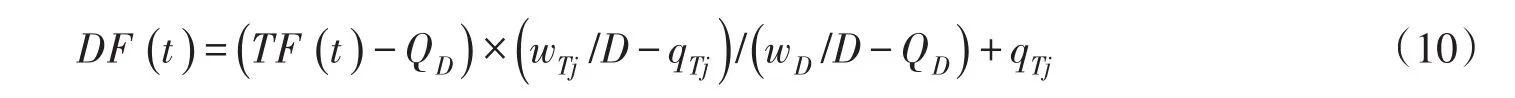
式中：DF(t)、TF(t)分别为设计洪水过程和典型洪水过程在t时刻的流量；QD、WD分别为典型洪水的洪峰流量和洪水历时D内的洪量；qTj、wTj分别表示联合重现期为T年时第j组样本求得的洪峰、洪量的最可能设计值。

这种方法不仅能完全控制洪峰和洪量的设计值，还可以较好地保持典型洪水过程的形状。

5　实例研究

清江属山溪性河流，是长江的主要支流之一，流域控制面积为1.7万km2，覆盖范围为东经108°35′～111°35′，北纬29°33′～30°50′。清江流域地形狭长，河道坡度较大，水流湍急，具有较快的汇流速度。清江流域的调节能力较弱，洪水峰形多样，既有常见的单峰和双峰洪水，也存在多次起伏的连续洪峰；清江的高峰洪水呈尖瘦形，也存在洪峰持续2～3 d的肥胖形洪水。隔河岩水库位于清江下游，距清江河口62 km，是一座以发电为主，兼顾防洪、航运效益的大型水利枢纽工程，具有年调节能力，防洪库容为5亿m3。隔河岩坝址的断面单峰历时一般为3～5 d，复峰可达10 d，一般选取7 d洪水过程进行水库防洪安全设计［11］。选用隔河岩水库坝址断面1951—2004年3 h流量系列，建立洪峰与7日洪量的联合分布，分析设计洪水估计及防洪调度的不确定性。

5.1边缘分布及联合分布的确定采用年最大值取样方法，获得隔河岩水库的年最大洪峰Q和7日洪量W，并采用线性矩法估计P-Ⅲ函数的参数。采用χ2检验法［6］对其进行假设检验，表1中为临界值，表1显示洪峰和洪量系列均通过了检验。为了选定拟合效果最优的Copula函数，采用Archime⁃dean族的G-H，Clayton和Frank函数建立隔河岩水库Q和W之间的二维联合分布，利用Kendall秩相关性系数法估计其参数，估计结果见表2。通过AIC准则、K-S检验和Cramer-von Mises检验方法［17］比较了不同Copula函数的拟合效果；图1给出了不同Copula函数对应的模拟序列和实测值的对比图。从表2和图1中可以看出，G-H Copula函数的拟合效果最优。

5.2单变量设计值及其不确定性通过上节估计的实测样本系列参数，求出隔河岩水库的洪峰和洪量在相应设计频率下的理论设计值，列于表3。为了研究抽样不确定性对边缘分布及单变量设计值的影响，采用Parametric Bootstrap法生成B=10 000组样本容量n=54（实测样本序列长度）的新序列。对于这10 000组新样本，以P-Ⅲ线型作为边缘分布函数，通过线性矩法估计其参数，分别计算洪峰和洪量的期望设计值及95%估计区间（表3），进而绘制出累计频率曲线（图2）。为了进一步评价单变量设计值的不确定性，通过下式计算了新样本序列估计值的标准差SD：

表1　隔河岩水库洪水统计特征值和P-Ⅲ型分布参数估计结果

表2　Copula函数的参数估计值及统计试验结果

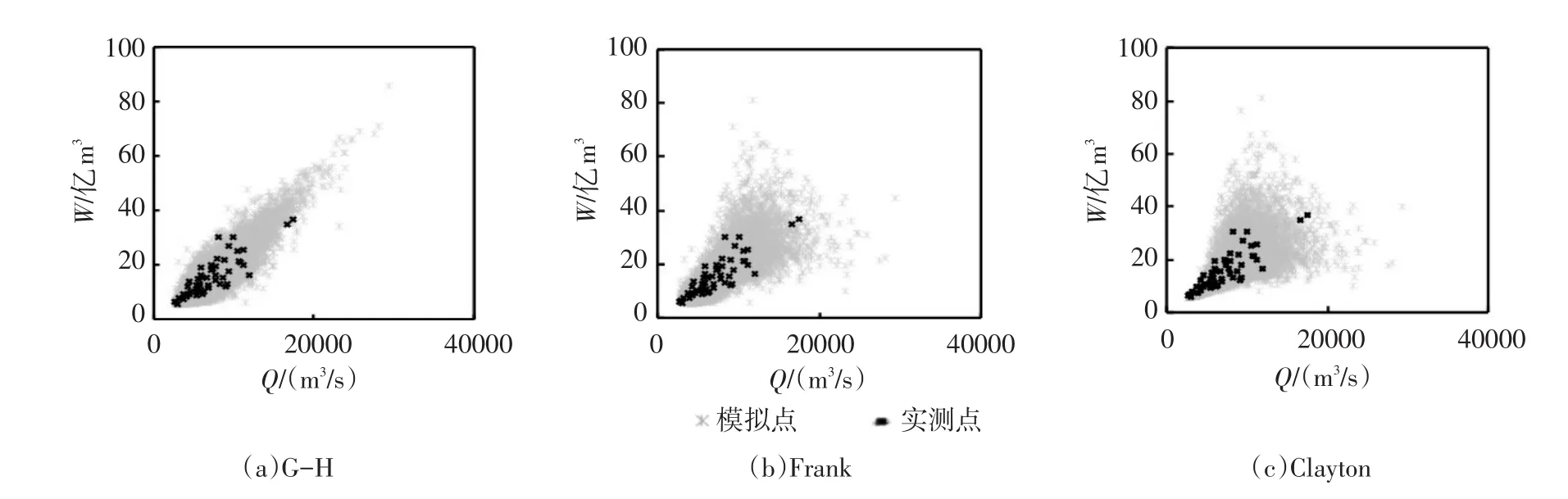
图1　隔河岩水库年最大洪峰和7日洪量实测值与模拟值对比

式中：xTj为采用第j组样本序列估计的重现期为TU时的设计值，表示重现期为TU时的期望设计值。标准差的计算结果也列于表3中。

从表3可以看出，采用原始序列计算的理论设计值与10 000组样本序列得到的期望设计值基本相同，这说明随机模拟方法能够较好地保持样本序列的基本特征。从表3和图2中还可以看出，设计值的95%置信区间几乎关于期望曲线呈对称分布；而且随着设计标准的提高，区间宽度和标准差逐渐增加，表明设计值的估计不确定性随着设计标准的提高而增大。图2和表3均显示了较大的不确定性，对于百年一遇设计值，洪峰和7日洪量的95%置信区间分别达到了8178 m3/s和25.0亿m3；标准差分别达到了2096 m3/s和6.4亿m3。

5.3两变量设计值及其不确定性选取不同的联合重现期TU，求解式（5）推求隔河岩水库设计洪水的最可能设计值。为了评价洪水最可能组合模式的合理性，取置信水平α=0.10，采用Volpi等［13］提出的两变量联合设计值区间估计方法推求不同联合重现期对应的置信区间。图3给出了采用历史实测数据得到的设计值和95%置信区间的估计结果。从图3看出，最可能设计值均位于95%置信区间内，说明它是一种较合理的设计值组合模式，适合用来描述隔河岩水库的洪水峰量特征。

目前，对于两变量估计的不确定性问题，一般选用小于样本容量的联合重现期作为研究对象［6-7，10］。本文以TU=20年为例开展研究，图3中的洪峰估计值（14 360 m3/s）和7日洪量设计值（35.27亿m3）比表3中单变量估计值分别偏大4.1%和5.0%，这说明传统单变量的估计值偏小、降低了防洪标准［11-13］。设置Parametric Bootstrap的模拟次数B=10 000，样本容量分别取n=54，n=100，n=150，n=200，采用C-PBU模型分别推求不同方案下的两变量设计值95%置信区域。本文设置不同的样本长度，是为了分析比较不同的模拟结果；样本容量n=54的方案代表了采用隔河岩水库实测数据估计联合设计值的不确定性。在工程案例中使用C-PBU方法推求估计不确定性时，应该设置样本容量与历史实测数据系列一致。图4中给出了采用历史实测数据得到的重现期等值线及理论设计值，并给出了对应于TU=20年的95%置信区域，表4给出了不确定性度量指标的计算结果。从图4和表4可以看出，95%置信区域的面积S、横向平均偏移幅度DQ、纵向平均偏移幅度DW和平均欧式距离d均随着样本容量的增加而减小，样本容量从n=54增加到n=200时，各项指标减小48%～60%，这说明样本容量对不确定性具有显著的影响。

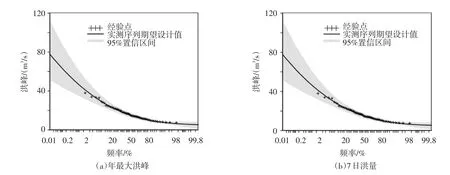
图2　隔河岩水库年最大洪峰和7日洪量实测序列累计频率曲线及95%置信区间

5.4调洪最高水位的不确定性就水库防洪安全而言，最重要的因素是坝前最高水位［2，8］。本文以调洪最高水位作为设计洪水影响水库防洪安全的重要指标，将联合设计值估计的两变量不确定性问题转化为单变量的不确定性问题，不仅更加直观合理，还能为水库运行调度提供决策依据。以TU=20年对应的10 000组最可能联合设计值（qTj，wTj）作为控制条件，分别采用偏不利和相似特征方法选取典型洪水过程，再通过变倍比放大方法推求模拟设计洪水过程线。提取隔河岩水库1951—2004年共54年的年最大场次洪水过程，用于相似特征方法选取典型洪水过程。下面以偏不利典型洪水为例，介绍设计洪水估计不确定性引起的设计洪水过程线不确定性。采用单变量设计值进行调洪演算，峰高量大、主峰靠后的1997年实测洪水为偏不利典型洪水过程［11］。图5给出了对应于TU=20的10 000组模拟设计洪水过程线。从图5可以看出，采用原始序列推求的设计洪水过程线处于模拟设计洪水过程线的中间位置。当样本容量为54年时，设计洪水过程线的不确定性显得尤其大；样本容量增加到200年时，设计洪水过程线的不确定性区间明显减小。

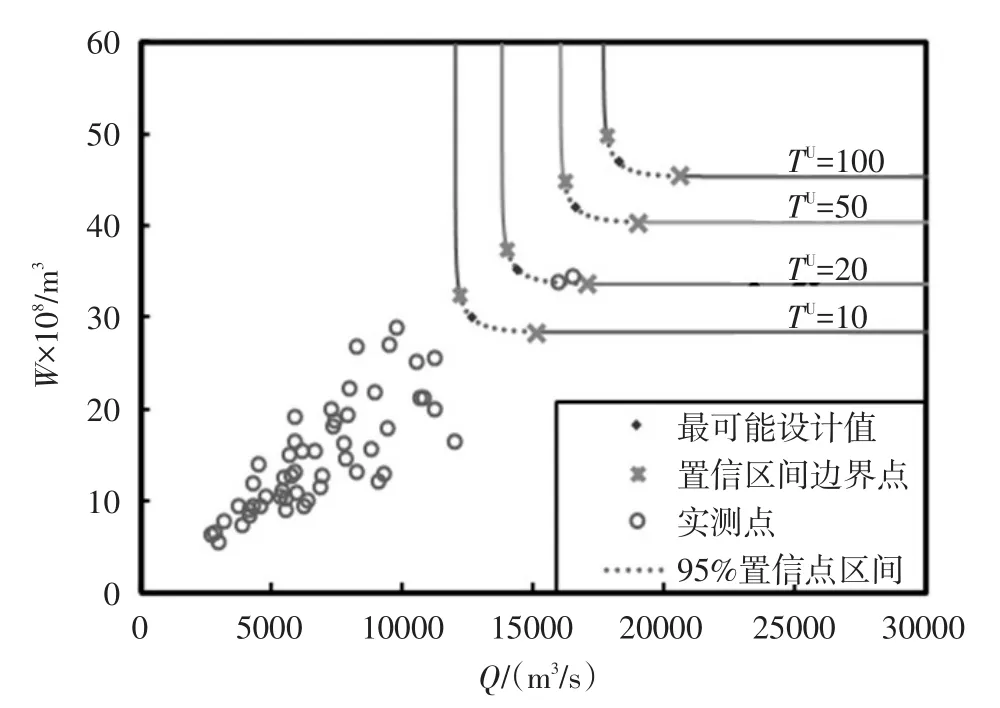
图3　隔河岩水库年最大洪峰和7日洪量联合设计值及95%置信区间

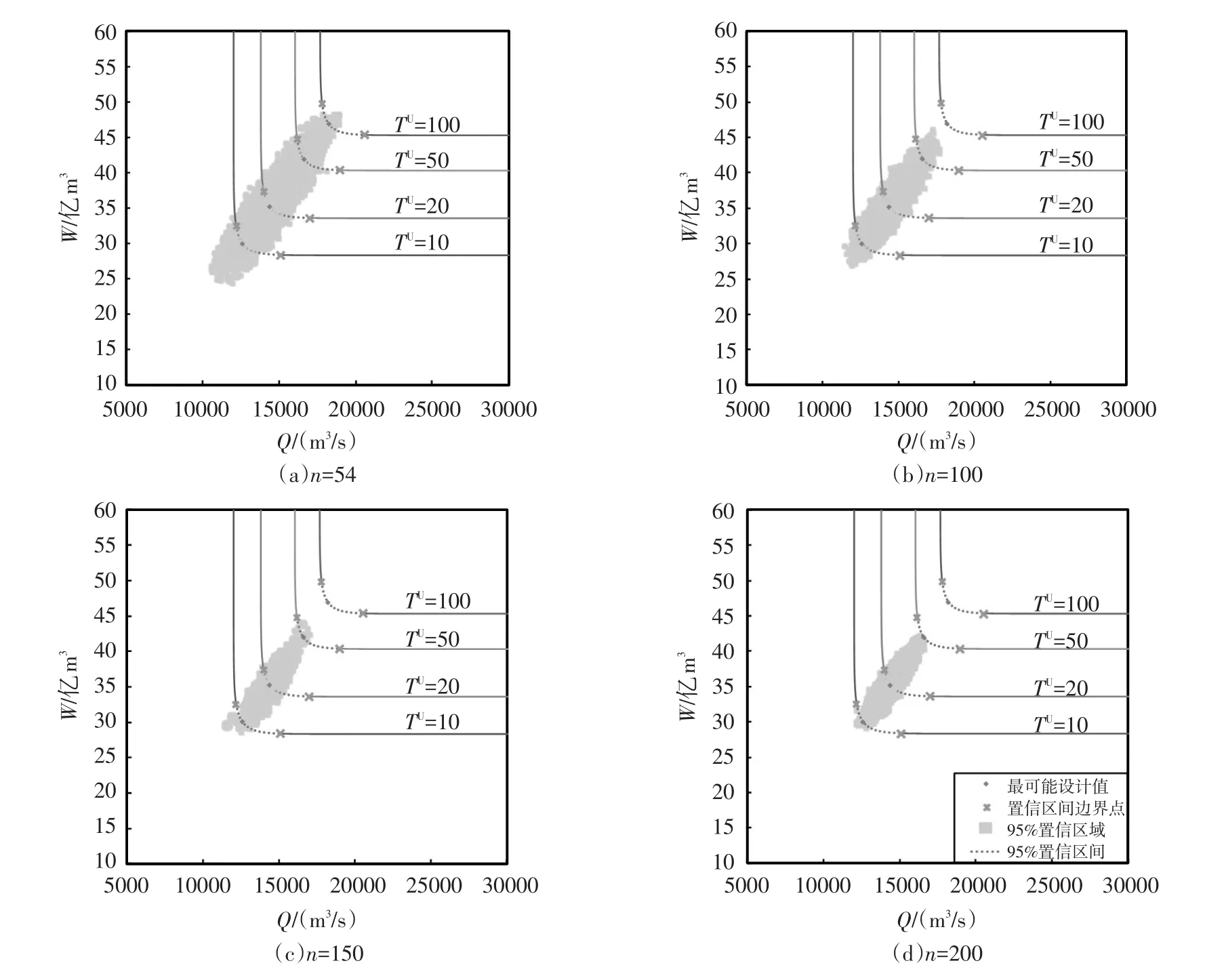
图4　隔河岩水库不同样本容量下TU=20对应的95%置信区域

表4　隔河岩水库不同样本容量下TU=20对应的不确定性度量指标结果

将上述两种方案下推求的设计洪水过程线，按照隔河岩水库的调度规则进行调洪演算，分别得到水库的最高调洪水位（Zmax），其方框盒须图如图6所示。表5给出了最高调洪水位的统计结果，从表5可以看出，在不同的样本容量下，通过选取相似典型洪水推求得到的最高调洪水位90%置信区间宽度和标准差均比偏不利典型方案下的统计值大，例如：在样本容量为100年时，前者比后者的区间宽度偏大4.8%，标准差偏大5.4%。这说明前者对54场洪水过程线进行了甄选，虽然增加了形状信息，但是也增加了调洪最高水位的不确定性。实际上，通过考虑洪峰洪量特征来选取典型洪水过程，虽然考虑了不同洪水典型的形状，具有一定的多样性，但是从表5中的水位信息来看，该方法也存在调洪结果可能偏于安全的问题，其是否适用需要根据工程的实际情况来考虑。在工程实践中，选取合理的洪水典型至关重要，对于强调防洪安全的水库而言，选取偏不利典型洪水过程操作简便，也减小了调洪结果的任意性和差异性。

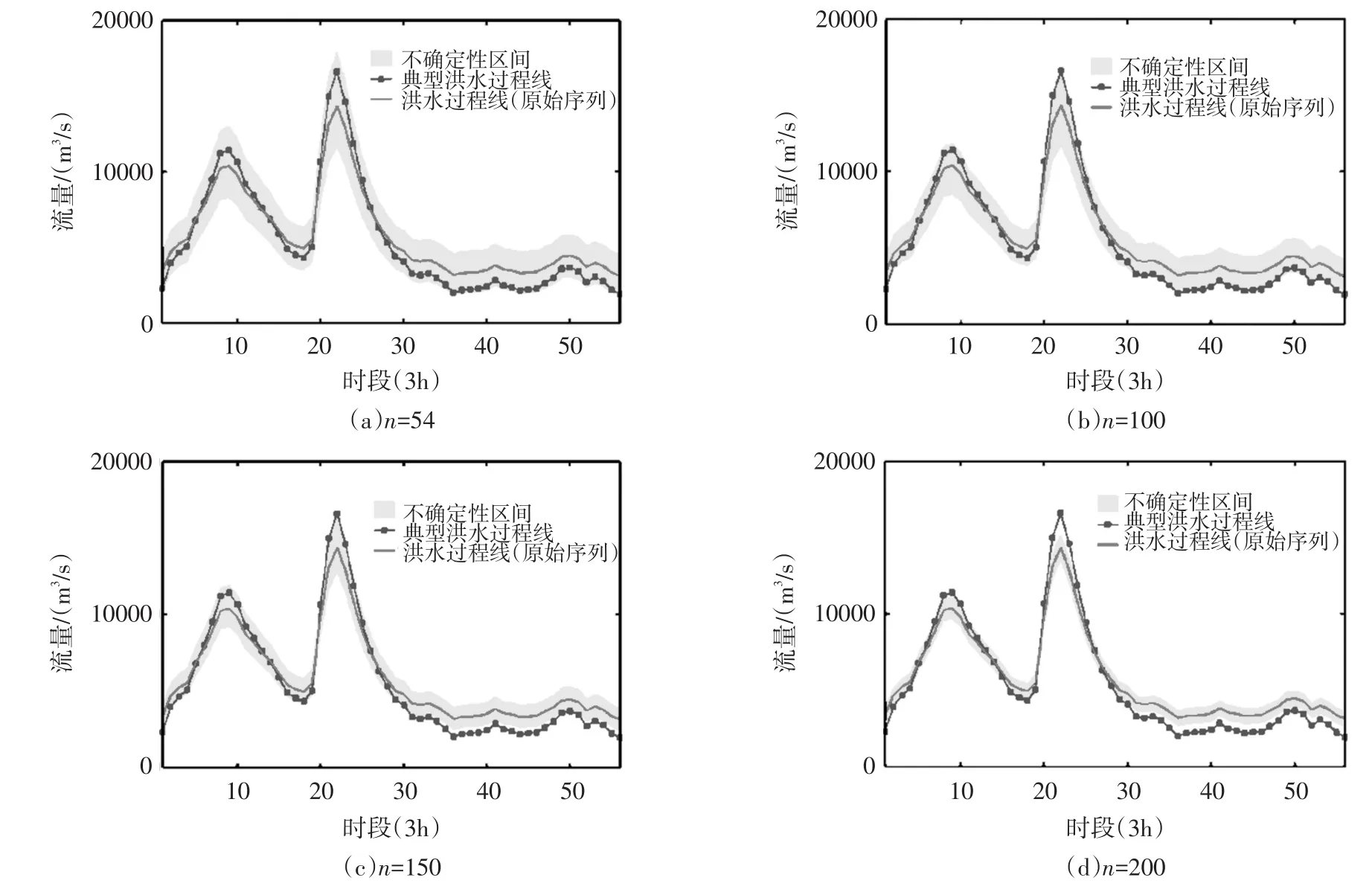
图5　隔河岩水库不同样本容量下TU=20对应的洪水过程线及其不确定性区间

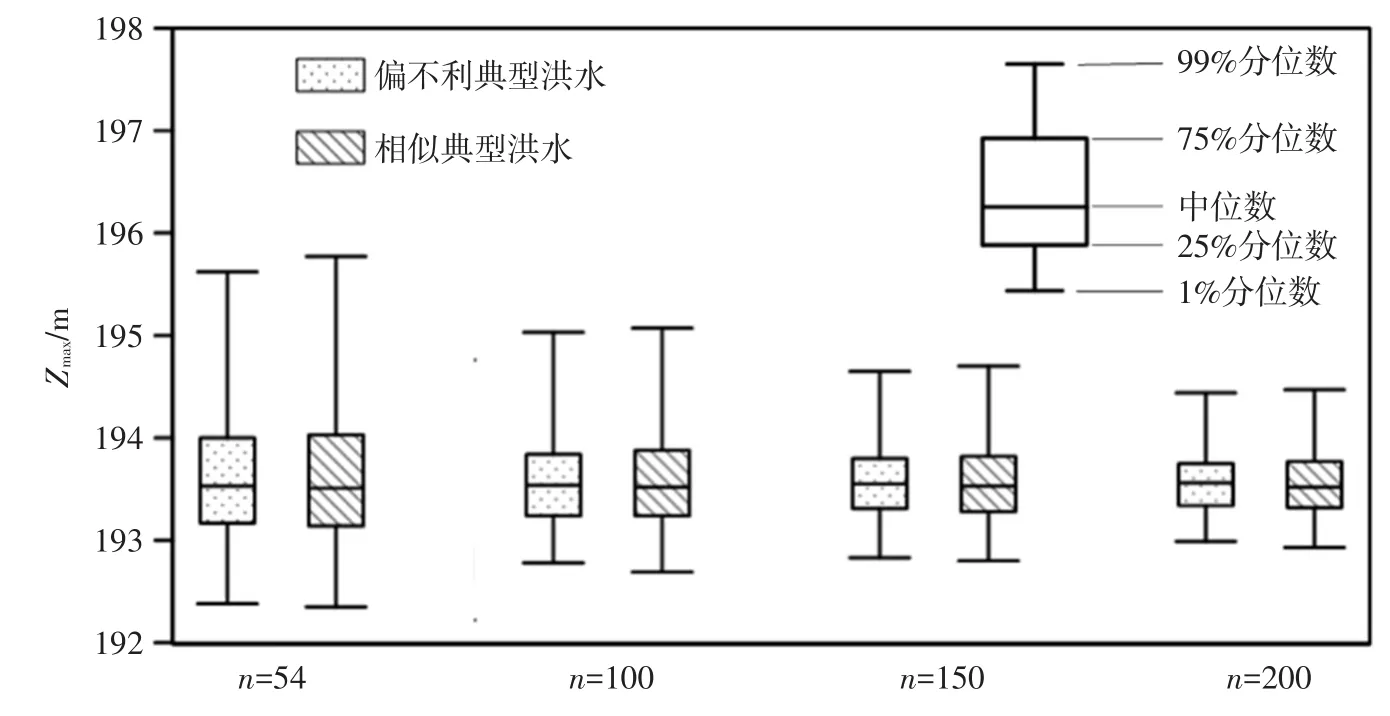
图6　隔河岩水库不同样本容量下TU=20对应的最高调洪水位

采用Dung等［7］的parametric bootstrap方法得到隔河岩水库TU=20年对应的联合设计值估计不确定性，并选择偏不利典型洪水过程（1997年实测洪水），通过调洪演算得到了最高调洪水位的不确定性区间如图7所示。对比分析图6和图7可以看出，当样本容量为实测序列长度（54年）时，两种方法模拟的最高调洪水位的90%置信区间宽度分别达到1.77 m和3.89 m，说明C-PBU模型考虑了洪水发生的最可能组合模式，有效克服了联合设计值随机取样引发的任意性和不确定性，结果比文献［7］方法更加合理可靠。

从表5还可以看出，样本容量小于100年时，两种方案下最高调洪水位的90%置信区间宽度均超过1.45 m，标准差则超过0.5 m，说明用于估计设计洪水的样本太小，对水库最高调洪水位产生了显著的不确定性。对于20年一遇洪水而言，只有样本容量超过200时，才能得到较可靠的调洪最高水位结果。一般情况下，水文序列均较短，工程实践中难以满足样本容量的要求，所以考虑设计洪水不确定性对水库防洪调度的影响至关重要。

表5　隔河岩水库最高调洪水位统计结果　（单位：m）

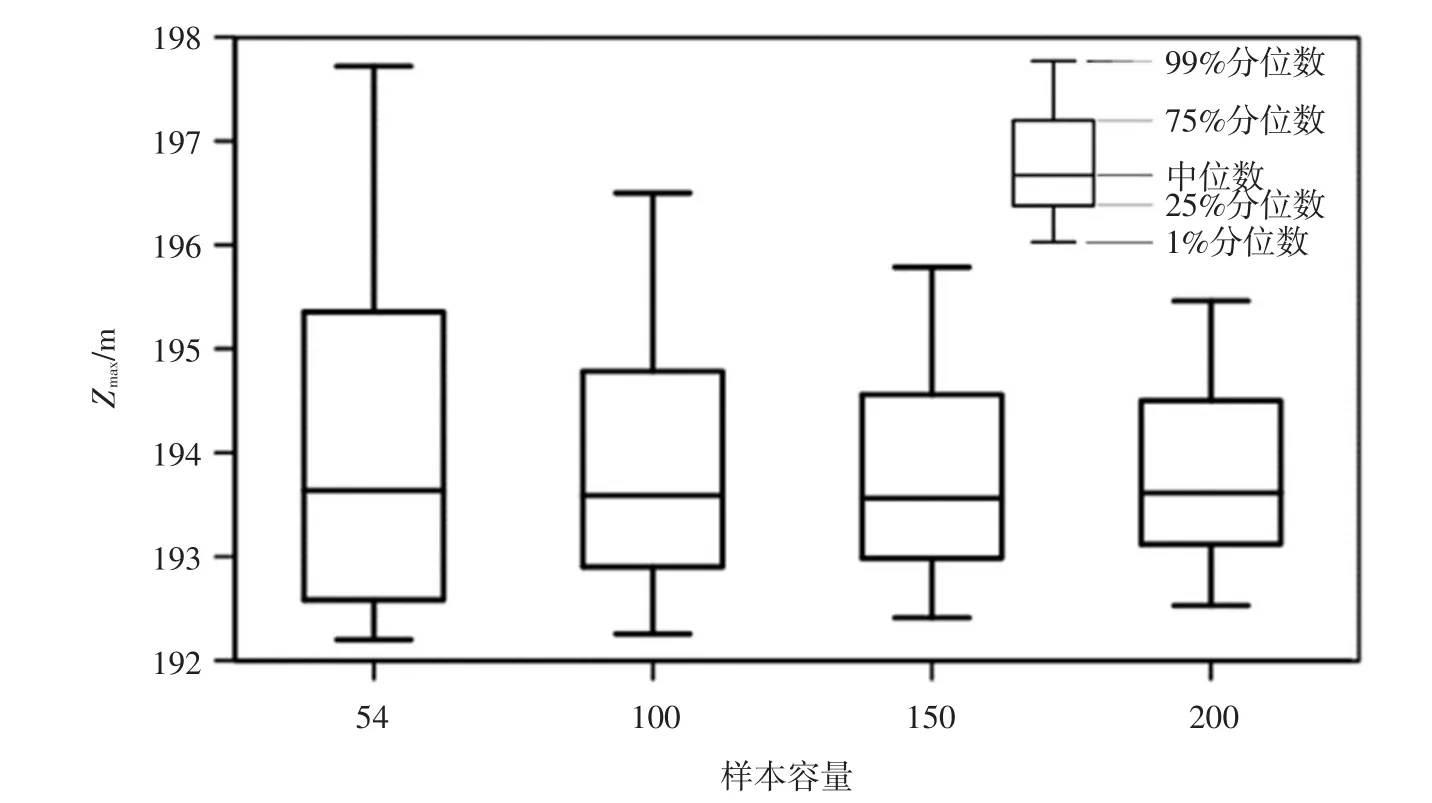
图7　文献［7］中parametric bootstrap方法推求的隔河岩水库TU=20对应的最高调洪水位

6　结论

本文考虑设计洪水峰量的最可能组合模式，建立了可描述两变量设计洪水估计不确定性的CPBU模型，同时提出了定量评价两变量不确定性大小的度量指标，分析了联合设计估计值、不同典型洪水选取的不确定性对水库防洪调度的影响。隔河岩水库的应用验证结论如下：（1）单变量设计值估计的95%置信区间随着设计标准的提高而增加。对于隔河岩水库的百年一遇设计洪水，年最大洪峰和7日洪量95%置信区间的宽度分别达到了8178 m3/s和25.0亿m3，这表明采用54年的样本序列估计单变量设计洪水存在相当大的不确定性。（2）在不同的样本容量下，通过选取相似典型洪水推求得到的最高洪水位90%置信区间宽度和标准差均比偏不利典型方案下的统计值大，说明偏不利典型模式有助于减小调洪最高水位的不确定性。（3）设计洪水估计的不确定性对水库防洪调度产生了显著的影响，而且显示了较大的不确定性。工程设计中的水文序列均较短，难以满足样本容量的要求，可以采用C-PBU模型推求置信区间，来考虑设计洪水估计不确定性对水库防洪安全的影响。