基于可行域搜索映射的并行动态规划

纪昌明，马皓宇，李传刚，李宁宁，俞洪杰

（华北电力大学 可再生能源学院，北京　102206）

1　研究背景

随着水电建设的持续推进，我国十三大水电基地已初具规模，大型水库群的陆续建成投产对我国的水电运行与管理提出了新要求。梯级水电站水库优化调度为充分利用梯级水库库容调节能力，对入库径流过程进行调节，制定梯级水库最优运行策略，是实现水电站效益增长的关键，其本质上是一个高维多重约束强耦合作用下的复杂非线性优化问题［1］。动态规划（DP）作为经典的多阶段优化算法，是求解梯级水库优化调度应用最广泛的优化算法，DP通过对复杂的多阶段组合优化问题分解，将优化调度问题转变为一系列结构类似的子问题并进行全局遍历寻优，以求得给定离散状态下的全局最优解［2］。因其对目标函数和约束条件形式的无要求以及对于复杂非线性问题解全局收敛性的保证而在水库调度中得到广泛应用［3］。

但随着经济建设和社会发展，水库群的规模不断增加，对优化调度结果的精度要求也不断提升。传统DP在求解梯级水库优化调度问题时，面临着计算量大、计算时间长的“维数灾”问题，其求解速度很难满足水库群调度的时效性要求。很多学者就此进行研究并提出一些解决方法，一部分学者通过对DP原理进行改进，提出基于DP的一系列改进算法，如张诚等［4］提出变阶段逐步优化算法用于梯级水电站的优化调度；史亚军等［5］针对梯级水库群优化调度中离散微分动态规划方法全局收敛性差及计算效率低的问题，提出了一种基于灰色系统预测方法的离散微分动态规划方法（GDDDP）；李亮等［6］建立了梯级水电站短期优化调度的数学模型，在此基础上探讨了逐次逼近（DPSA）和大系统分解协调两种降维算法的主要思想和实现方法。另一部分学者通过缩减传统DP的搜索空间，以减少计算量，如明波等［7］基于发电调度模型中水电站最小出力及下泄流量约束，提出搜索空间缩减法并将其与智能算法相耦合；冯仲恺等［8］提出了集成水库群优化调度多重复杂运行约束的知识规则降维方法；赵铜铁钢等［9］在“边际效用递减”的假设下分析得到两阶段水库调度中本时段泄水量、下一时段余留水量与本时段初水库蓄水量间的单调增加关系，将这一单调关系由两阶段推广到多阶段水库调度并进一步提出动态规划算法改进：搜索域缩减算法和邻域搜索算法。对前者而言，改进方法大多通过牺牲解的全局最优性以节省计算时间，且最终结果受初始轨迹影响较大，计算所得水库运行策略劣于传统DP；对于后者而言，所提出的搜索空间缩减方法通用性不高，且可能增加算法复杂度。

为解决上述问题，本文在对动态规划处理调度问题原理和算法约束处理机制深入研究的基础上，提出基于可行域搜索映射的动态规划算法：在约束处理问题上引入映射思想，提出可行域搜索映射，通过对当前时段多重约束的分析，得出时段可行搜索空间，仅对可行域内的状态组合进行计算，以规避无效系统状态计算，缩减算法运行时间，完成对传统DP的改进；接着通过对动态规划的并行性分析，以.NET并行拓展库为技术支撑，对基于可行域搜索映射的动态规划算法实现并行化，以进一步提升算法运行速度；最后，以李仙江流域三库调度为研究实例，验证算法的科学与实用性。

2　水库优化调度模型

梯级水电站发电量最大模型是最为常见的梯级水库优化调度模型，该模型可描述为在已知未来一个调度期内各水库始末水位、梯级水库入库径流以及区间径流的情况下，考虑库容、出力、下泄流量等约束条件，寻求梯级水库群的最优调度决策，使调度期内系统的发电总量最大，其目标函数与约束条件如下［10］。

2.1目标函数

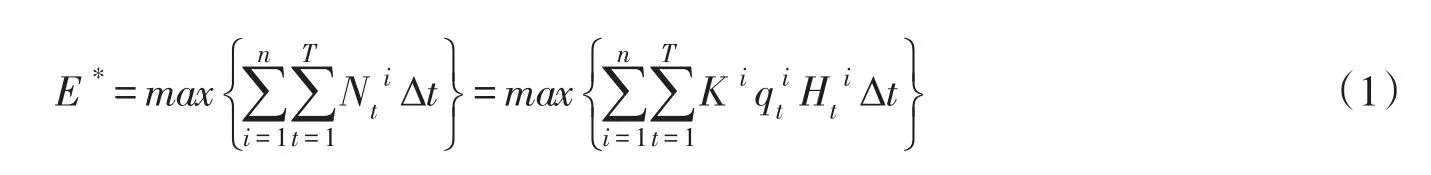
式中：E*为调度期内的总发电量；为t时段i电站的出力；n、T分别为电站总数和调度期时段总数；Δt为单位时段长度；为i电站的出力系数；为t时段i电站的平均发电流量；为t时段i电站的平均水头。

2.2约束条件水量平衡约束：

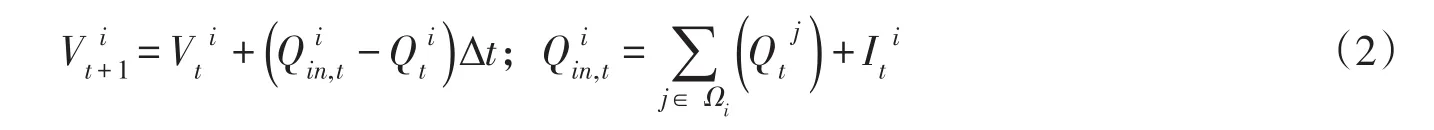
水位库容曲线约束：

下游水位流量曲线约束：

库容约束：

出力约束：

式中： fyxcl为预想出力函数。

下泄流量约束：

2.3模型求解DP求解水库群优化调度问题，通常将调度期（一年或数年）按月或旬分为T个阶段，从而将调度问题看作一多阶段决策问题，通过逆时序递推将多阶段决策分解为多个单阶段决策进行处理，然后通过顺时序递推获得水库群的最优策略［11］。其求解步骤如下（计算流程见图1）：

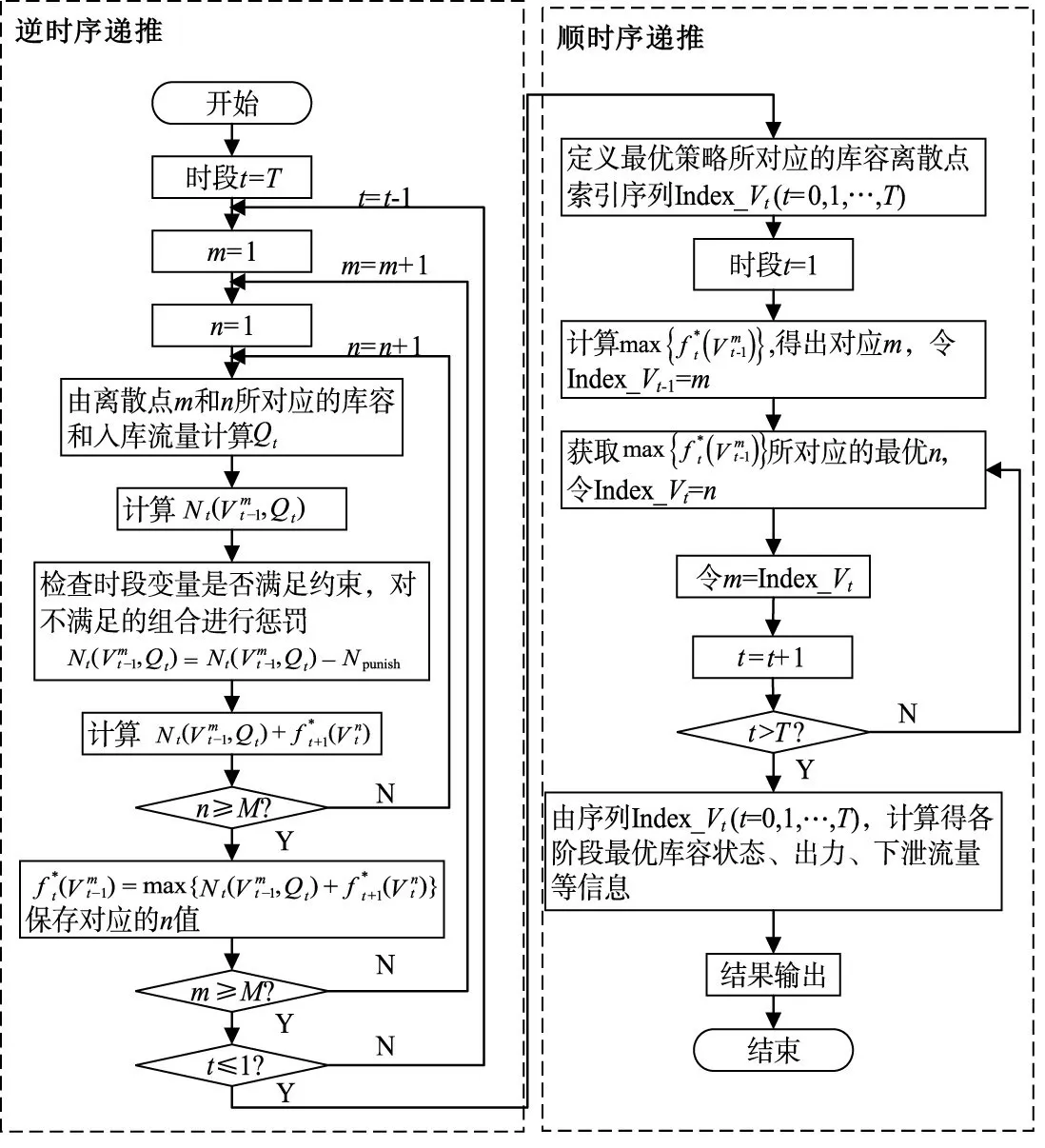
图1　DP计算流程

逆时序递推计算：根据式（9），按逆时序从调度期阶段末（阶段T）递推至阶段初（阶段1），推求出满足阶段约束条件下各阶段出力及最优余留期效益，对不满足约束的状态组合的指标函数添加惩罚项予以惩罚。逆时序递推方程如下：

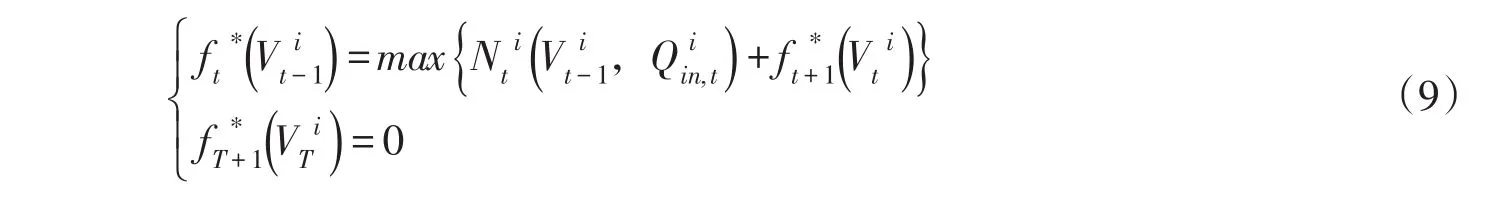
顺时序递推计算：依据逆时序递推所得最优余留期效益及对应的库容路径，顺序递推得最优策略及对应的各阶段最优状态。

2.4传统DP搜索域及计算模式分析一方面，DP算法对于约束条件的处理机制一般是通过惩罚函数法，在递推计算过程中，先不顾及状态组合是否满足时段约束，对单阶段所有库容组合遍历求解时段出力值，计算完出力、流量等信息后，利用时段约束集合对出力等时段调度信息一一进行检验，对不符合约束的状态组合进行惩罚，将惩罚项纳入时段出力构成指标函数，从而引导算法所得解逐步转向可行区域。而这种盲目的遍历状态组合行为正是造成动态规划计算量大、耗时长的原因之一，且水库调度中惩罚因子的选取比较困难，往往需要根据实际问题通过试算获取，使得算法建模困难。罚函数计算公式如下：

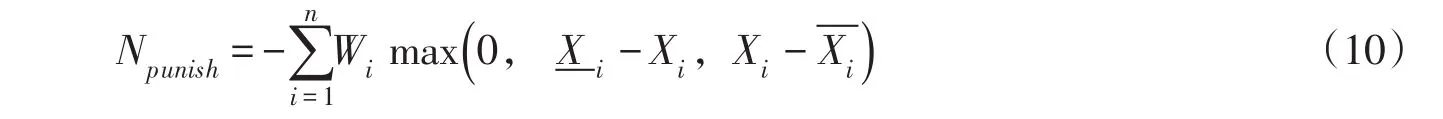
式中：Npunish为约束违反惩罚项；Wi为针对第i项约束的惩罚因子；Xi为第i项约束所限制的调度变量；和分别为第i项约束的上、下限。

另一方面，DP算法属于典型的循环串行计算模式，当水库数量大于2或库容离散点数量较多时，很难在合理时间内获得满意优化结果，无法满足水电计划编制的时效性要求，串行计算模式导致总任务积压在计算机的单个内核上，未充分利用多核CPU及超线程计算的优势，造成计算机资源的闲置浪费及内核利用效率低下。

故本文拟将映射和并行计算思想引入水库调度的计算过程中，通过构建基于可行域搜索映射的并行动态规划模型，精简约束处理机制，并行化DP算法中的热点部分，在保证解全局收敛性的前提下提高程序运行速度与效率。

3　可行域搜索映射

3.1映射概念映射是对定义在实数域上的函数概念向更一般的集合关系的推广。数学中对其严格定义为：设A、B为两个非空集合，若存在一个法则，使得对A中的每一个元素a，按法则f，在B中都有唯一确定的元素b与之对应，则称f为A到B的映射，记作：f：A→B，映射将函数定义中两个集合从非空集合扩展到任意元素的集合［12］。本文将映射的思想运用到调度问题的可行域辨识中：

式中：（L0，L1，L2，…）为水库调度阶段约束集合，其中任意约束Lk可表示为（lk1，lk2）的向量形式，lk1、lk2为针对相应调度变量的约束边界；F为阶段约束集合转化为仅针对单变量如状态变量库容或决策变量下泄流量的约束，表示为（f1，f2）的向量形式，f1、f2为约束边界。

满足阶段约束集合的泄流情况可能有很多，F通过向量（f1，f2）以区间的形式将这些情况均涵盖在内。当阶段约束集合确定时，其对应的F也是唯一确定的，两者间的关系满足三性要求（有序性，存在性，唯一性），故F与约束集合间的对应关系f为映射，本文将其称作可行域搜索映射。在递推计算过程中，传统DP的单阶段搜索域为所有库容离散点，而本文拟借可行域搜索映射f，将阶段内针对出力、流量、库容等不同变量的复杂各异约束转化精简为针对库容的总约束，仅对约束范围内的库容离散点组合进行遍历计算。传统DP和经f处理后的单阶段搜索空间如图2所示。

3.2优化调度约束条件等级划分梯级水库作为兼具多重社会属性的水资源利用载体，除满足自身安全稳定运行外，还需肩负水库所在流域的各部门综合利用需求，在水库优化调度中，这些利益诉求转化可为针对不同调度变量的约束。在某些特定条件下，这些约束之间可能产生冲突，其本质为各部门关于水库的利益冲突［13］。例如在枯期，水库运行水位较低时，若水库为满足水电站保证出力要求进行下泄，可能导致时段末水位低于最低水位限制，此时出力约束与水位约束便产生冲突，从集合论角度，即两者对应空间无交集。故在建立映射之前，需要对约束集合进行整理归类。本文在阅读并总结大量水库调度文献约束处理方式的基础上［14-16］，将时段约束分为三等：一等约束为通过水库长期观测资料以及为保证水库安全稳定运行所建立的约束，其为水库优化调度的前提条件和基础，要求必须遵守；二等约束为防洪、用水及生态等部门对水库下泄流量设定的约束，其目的是为了保障下游防洪对象的安全和河道用水需求；三等约束为发电部门为了满足电网调峰需求与发电部门的效益对电站时段出力设定的约束。当调度过程中约束条件相互矛盾时，优先满足高等级约束，等级划分如下：（1）一等约束：水量平衡约束；水位库容曲线约束；下游水位流量曲线约束；变量非负约束；库容约束；（2）二等约束：下泄流量约束；（3）三等约束：出力约束。

3.3可行域搜索映射模型基于集合论思想，建立可行域搜索映射模型：假定DP算法采用逆时序递推方程（也可采用顺时序递推方程），在单阶段计算过程中，已知入库流量Qin，t和时段初库容Vt，将此作为已知条件约束L0，综合考虑多种约束，将其耦合转化为下泄流量Qt的约束，整个推求过程如下所示。

（1）一等约束转化为集合U1。一等约束集合中，水量平衡约束作为时段初末状态转移方程使用，水位库容曲线约束与下游水位流量曲线约束作为变量间相互转换的基础约束使用，变量非负约束要求下泄流量值非负。在已知入库流量和时段初库容的情况下，由水量平衡约束可知，下泄流量与时段末库容成反比，由此可将库容约束转化为Qt约束。取变量非负约束和库容约束的交集得U1：

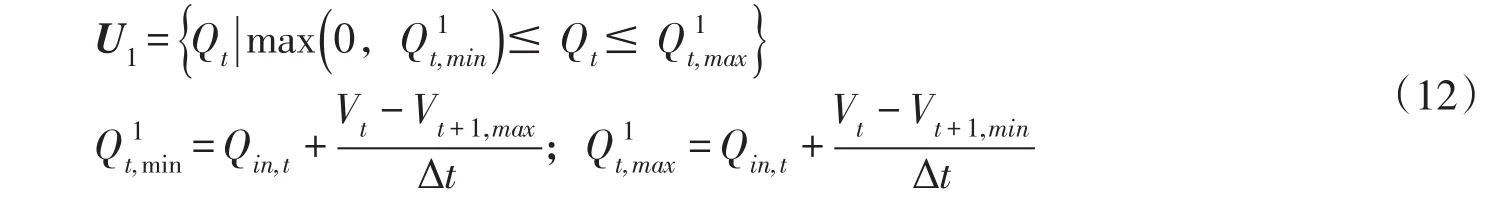
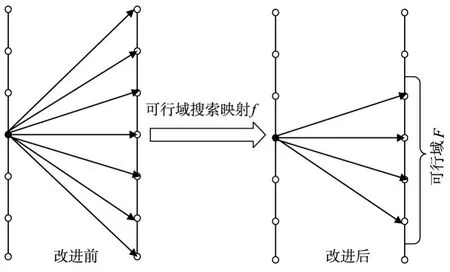
图2　传统DP与f处理后的单阶段搜索空间

（2）二等约束转化为集合U2。将为了保障下游防洪对象的安全和最低限度河道用水的下泄流量约束作为约束集合U2：

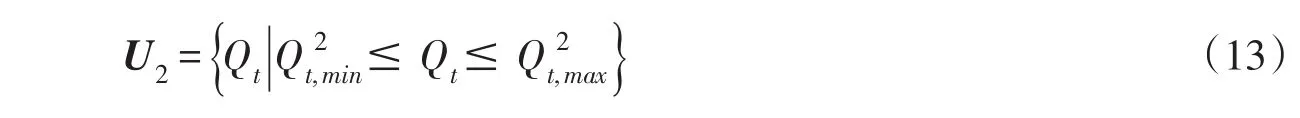
（3）三等约束转化为集合U3。为将出力约束转化为等价的流量约束，需对两者间关系进行分析。出力计算公式为：

暂不考虑电站出力能力限制，则Nt与Qt和Ht存在直接联系，Ht和上游平均水位Hu，下游平均水位Hd及水头损失ΔH有关，而这三者与Qt均联系密切，关系如下：

式中：α为水头损失系数。当入库流量和时段初库容均为常数时，Ht实际上仅与Qt成函数关系，故Nt仅与Qt成函数关系，进一步推导Nt的一阶和二阶导数：

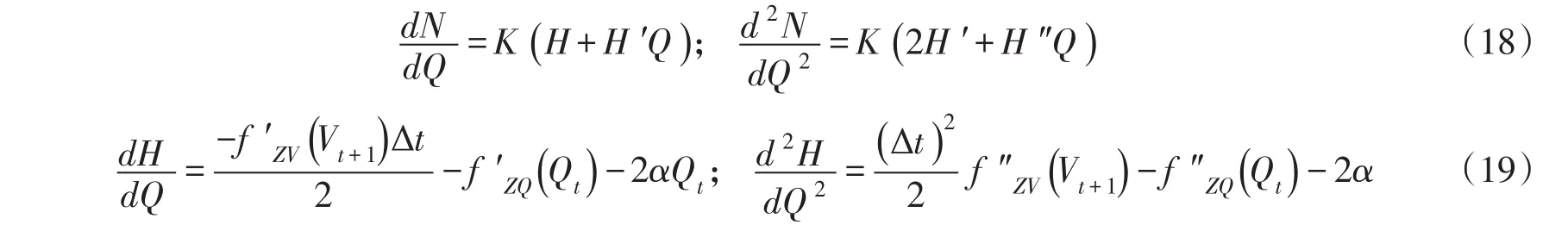
通常，水位库容曲线 fZV和下游水位流量曲线 fZQ可通过幂函数表示：

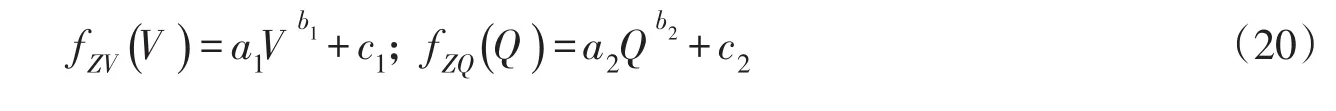
同时， fZV和 fZQ满足：

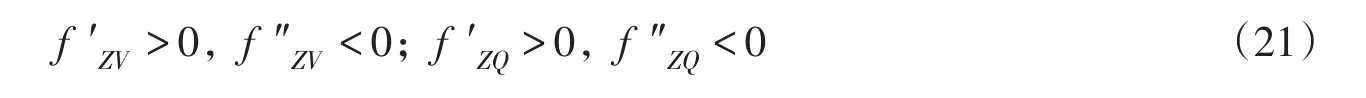
式中：a1、a2、b1、b2、c1、c2均为常数，a1、a2、b1、b2为正常数，同时b1、b2小于 1。

由式（18）—（21）可知N″＜0，而无法判断N′的正负，为此采用极端条件法进行分析：假定Qt=0，Nt=0，此时N′＞0；Qt由0开始增加，此时水电站存在一定水头和发电流量，Nt＞0；Qt的大小增至一定程度，出力受到预想出力限制，而预想出力大小随下泄流量的增加而减小，故出力随下泄流量的增加而减小，此时N′＜0。

由此可得N′随着Qt的增加，经历了大于0，等于0和小于0三个阶段，且N″＜0，故N与Q的函数图像关系是拟抛物线型，见图3。

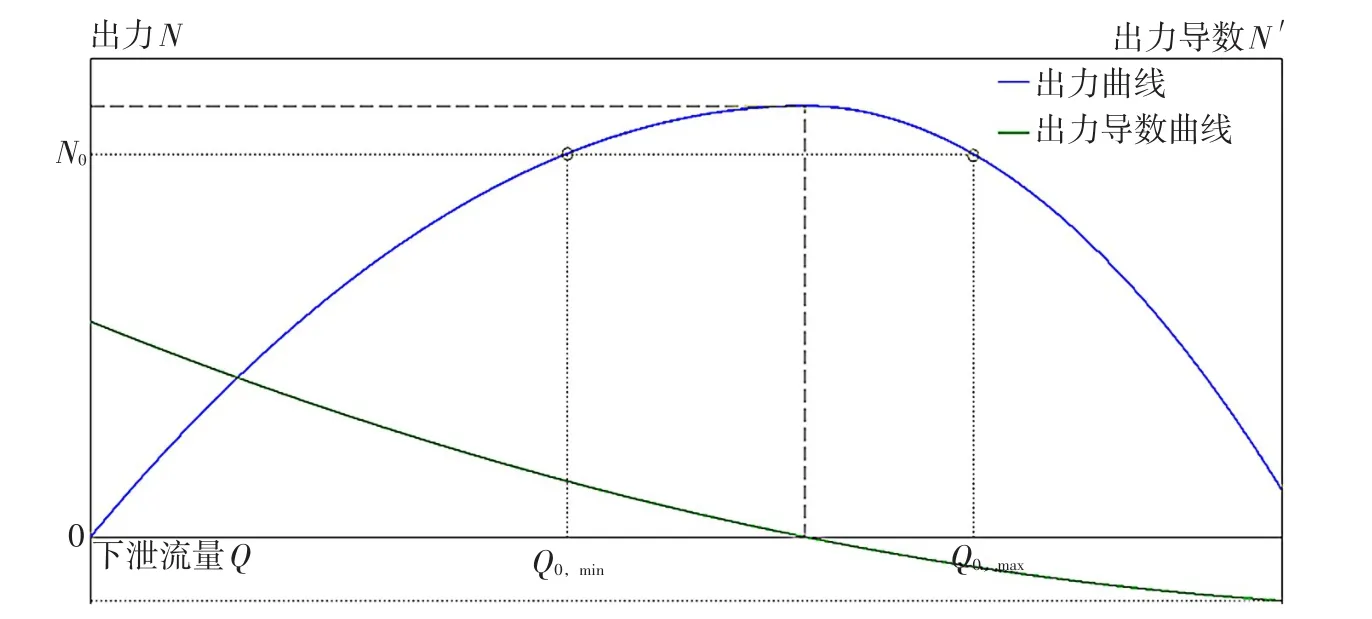
图3　电站出力曲线和一阶导数曲线

若曲线连续，对一个出力值N0，有两个流量值Q0，min、Q0，max与之对应，而实际调度过程中，由于机组出力特性的限制，曲线连续性得不到保证，而Nt与Qt间又存在着复杂的非线性联系，难以通过解析式的形式表达两者间函数关系，在已知Nt情况下，通常利用试算法推求Qt，两者间关系用fNQ表示。利用fNQ，将出力约束转化为下泄流量约束U3：

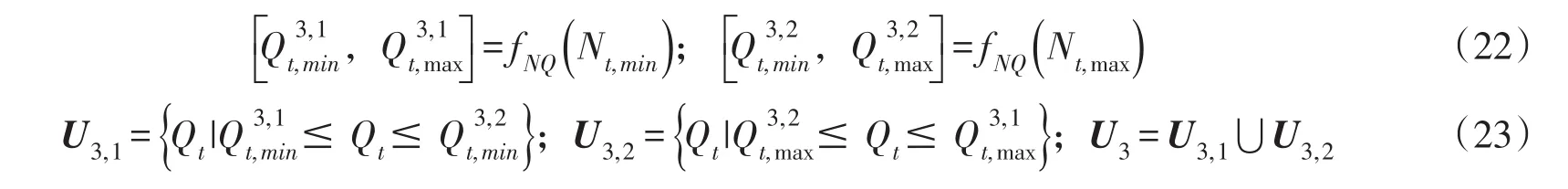
（4）约束条件耦合。由集合论可知，集合的交集满足这些集合的所有特性，前文将约束条件转化为下泄流量的约束{U1，U2，U3}，令集合W1=U1，W2=U1∩U2，W3=U1∩U2∩U3。固定入库流量不变，对所有时段初库容离散情况进行遍历，计算并存储集合{W1，W2，W3}。若所有W3皆为空集，则认为在此入库流量条件下，三等约束无法满足，优先满足W2，并将其作为下泄流量Qt的最终约束，否则，将W3作为最终约束；当所有的W3皆为空集，若W2也为空集，则认为在此条件下，三等和二等约束条件均得不到满足，优先满足W1并将其作为最终约束，否则，将W2作为最终约束。最后通过水量平衡方程将下泄流量约束转化为时段末库容约束F，以方便递推计算过程中可行状态的识别。

3.4可行域搜索映射计算步骤实际调度过程中，要求程序对输入信息做出快速准确响应，在已知时段约束集合条件下，希望能快速完成约束精简合并，得出易于辨识的可行域范围，这就要求计算获取f的解析式形式。在DP的逆时序递推计算中，入库径流、时段初库容作为已知约束条件L0，其余时段约束条件统记为Lt，映射关系记为：F=f（L0，Lt）。

由3.3节可知，f涉及多个非线性水库特征曲线及逻辑关系判断，其解析式的具体形式很难给出，为此，本文采用离散值法求得f所对应的多维空间曲面，即计算不同时段（对应不同时段约束集合），不同入库流量与时段初库容组合下的可行空间F，计算步骤如下：（1）令当前时段t=1，对应约束集合Lt；（2）对水库的历史入库流量资料进行统计，得最大与最小历史入流值，并将入库流量Qin，t在两者之间离散为N个点；（3）将时段初库容Vt在库容约束的最大和最小值之间离散为M个点；（4）根据3.3节模型，得出时段t不同Qin，t与Vt组合下的时段末库容约束F，并利用SQLService对结果（包括t，Qin，t，Vt，F）进行存储；（5）进行判断，t是否大于调度期阶段数T，若是则停止迭代，得到可行域搜索映射并已将其存储于数据库中，否则令t=t+1，返回步骤（3）继续进行计算。

计算完毕后，在已知调度期时段、入库流量及时段初库容的情况下，通过查询数据库存储的映射f，则可得到时段末库容约束，若出现入库流量、时段初库容的值与曲线内的点不对应的情况，则调用3.3节的模型进行在线计算，实际应用过程中，当入库流量、时段初库容的离散精度较高时，可直接查得库容约束，这就实现了时段复杂各异约束集合的快速合并简化。当离散精度较大时，曲线计算量也随之增大，但对于水库而言，当步入稳定运行阶段后，调度期内的时段约束集合类型数远小于时段数，且曲线为离线计算模式，曲线内的数据存储在计算机外存，故不仅不会增加调度程序的计算时长与内存负担，而且通过数据库查询可直接获得可行搜索空间，将大幅减免系统在非可行状态区域内的无效搜索，提高运行效率，故可行域搜索映射的计算与运用将满足实际工程的需要。

3.5基于可行域搜索映射的改进DP基于可行域搜索映射的改进DP算法主要步骤如下：

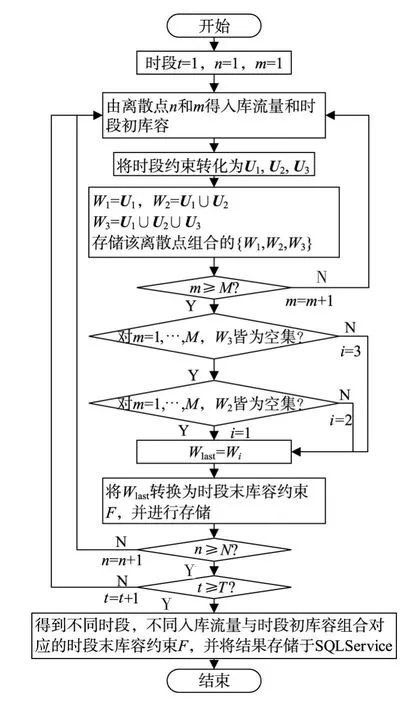
图4　可行域搜索映射计算流程

（1）将调度期离散为T个时段，时段索引为t，库容在库容限制范围内离散为M个点，时段初库容索引为m，时段末为n；（2）令t=T，m=1；（3）令n=1，根据时段、入库流量和时段初库容，查询数据库得时段末库容约束F（t，Qt，）；（4）检查离散点n所对应的时段末库容是否满足F，当n≤M，若满足F，则对出力与余留期效益进行计算，令n=n+1，继续进行步骤（4），若不满足，则n=n+1，继续进行步骤（4）；当n=M+1，转至步骤（5）；（5）对时段初离散点m对应的余留期效益进行比较，求得m对应的最大余留期效益值当m=M+1，转至步骤（6），否则令m=m+1，转至步骤（3）；（6）若t=1，则逆时序递推计算完成，否则，令t=t-1，转至步骤（3）；（7）按逆时序递推所求得的最优余留期效益及对应库容路径，顺时序递推求得最优调度策略。

由上述计算步骤可以看出，本文提出的基于可行域搜索映射的改进DP算法，和现行的可行域搜索方法相比，有以下几点优势：针对某时段，入库流量和时段初库容的组合求取时段末库容的可行区间，易于程序对可行区域进行识别，且保证无效状态组合的剔除，进一步缩小可行搜索域；对常见的时段约束条件进行等级排序，更符合实际工程情况，且防止约束交集为空集的情况；提前完成可行搜索空间的计算并将结果存储于数据库中，不需要每次在调度程序运行前进行重复计算。

4　基于可行域搜索映射的并行动态规划

传统动态规划通过顺序式代码实现，指令的依次执行无法发挥计算机的多内核优势，为进一步缩短计算时间，将并行算法设计引入到本文提出的基于可行域搜索映射的动态规划算法，以额外的内存消耗换取计算效率的提升，即利用多个内核或处理器在同一时刻同时处理多个计算子任务。

4.1动态规划并行性分析梯级水库DP优化程序中最耗时的部分是出力和余留期效益的递推计算过程，该部分包含三层循环，最外层为遍历调度时段的阶段循环，中间层为遍历时段初库容离散点的时段初循环，最内层为遍历时段末库容离散点的时段末循环。由DP递推公式可以看出，余留期效益为时序累加，其计算与余留时段相关，而时段间出力计算与余留时段无关，阶段循环由于余留期效益计算而具有顺序依赖性，无法直接实现并行。一些学者提出将阶段循环中的出力计算与余留期效益计算相分离，实现阶段循环并行［17-18］。该方法虽然可行，但需要存储各阶段所有状态组合的出力计算值，将耗费大量内存空间，因此本文不采用阶段循环并行。由于单阶段库容组合间的计算相互独立，故时段初与时段末循环具有天然的并行性，可从此两者入手实现并行，但若在时段末循环处并行，并行总任务规模较小，而实现并行的通信花销较大，导致内核利用率较低。

4.2并行化实现基于4.1节的分析，本文决定采用时段初循环并行模式，以实现基于可行域搜索映射的并行动态规划。利用.NETFramework 4的并行拓展库（Parallel extensions）进行任务分配以提供负载均衡的潜在并行执行。图5为算法并行示意图，M为库容离散点数，n为水库数目，利用C（k，t）表示t时段初梯级水库的库容状态组合，将其作为t时段初状态，利用C（k′，t+1）表示t时段末梯级水库的库容状态组合，将其作为t时段末状态，k和k′代表时段初和时段末库容组合的序号，k，k′∈［1，Mn］，（C（k，t）， C（k′，t+1））表示t时段梯级水库的时段初末状态组合，将参与并行的内核数记为P。在时段初循环处将所有时段初状态对应的库容组合计算作为总任务，对应计算机内核数P，将总任务划分为P个子任务：{（C（k，t），C（k′，t+1））|k∈kp，k′∈［1，Mn］}，p=1，…，P，kp为分配给内核p的t时段初状态的子集。每个内核p负责其子任务所对应的库容组合的最优余留期效益和最优库容转换的计算与存储，同时对于每一个k，可通过可行域搜索映射得到时段末库容约束F，利用F在时段末循环处将不符合阶段约束的C（k′，t+1）剔除以减少计算量，即将每个内核的子任务由{（C（k，t），C（k′，t+1））|k∈kp，k′∈［1，Mn］}缩减至{（C（k，t），C（k′，t+1））|k∈kp，k′∈［Wk，start，Wk，end］}。

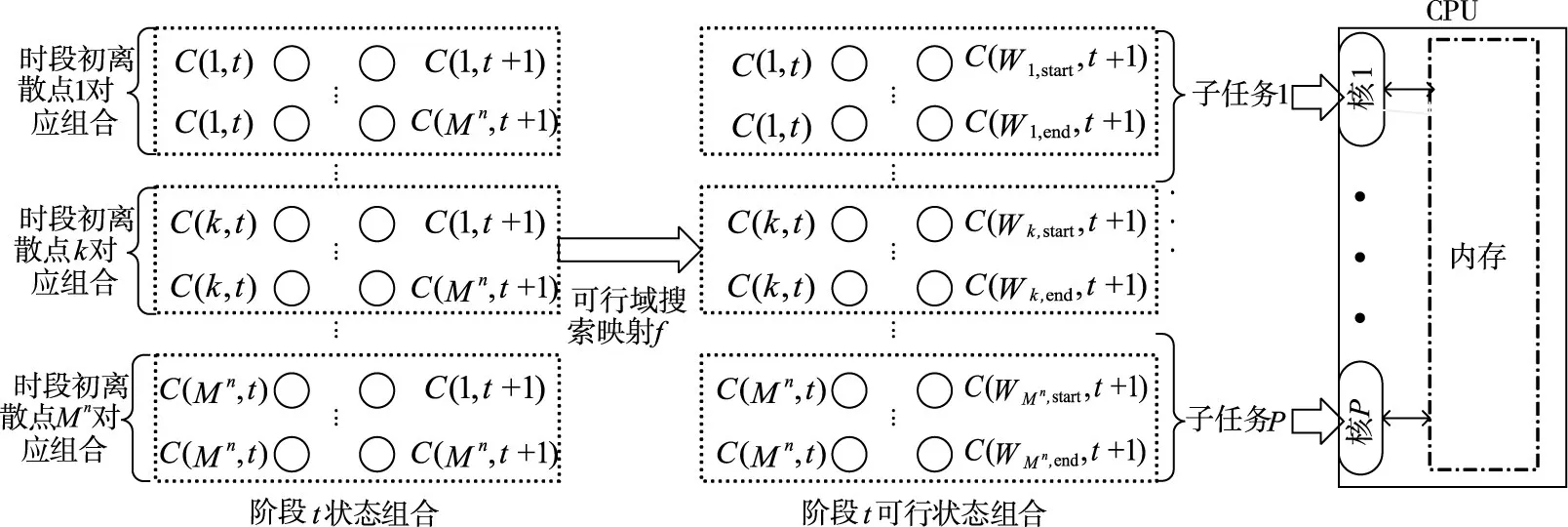
图5　算法并行示意

4.3并行性能评价指标完成算法的并行化后，其并行效果的评价同样是一项重要工作，本文采用加速比和并行效率这两个最常用的性能评价指标完成并行计算模式的评价。

加速比是指同一个计算任务以并行模式和串行模式运行消耗的时间比率，用来衡量程序并行化后相对于原来顺序执行的加速倍数。假设程序在串行模式下的计算时间为Ts，在并行模式下的计算时间为Tp，p为参与并行计算的处理器数，则加速比Sp定义为：

并行效率是指加速比与处理器数的比率，用于衡量并行模式中处理器的有效利用程度，实际计算中并行效率Ep通常小于1，定义为：

5　实例分析

李仙江干流规划按照7级开发，从上到下共开发完成了7座水电站：崖羊山、石门坎、新平寨、龙马、居甫渡、戈兰滩和土卡河，总装机容量达到148.5万kW。本文选取具有调节性能的崖羊山、石门坎和龙马作为实例研究的梯级水电站水库系统，三库联合调度关系如图6所示，三库基本参数信息见表1。

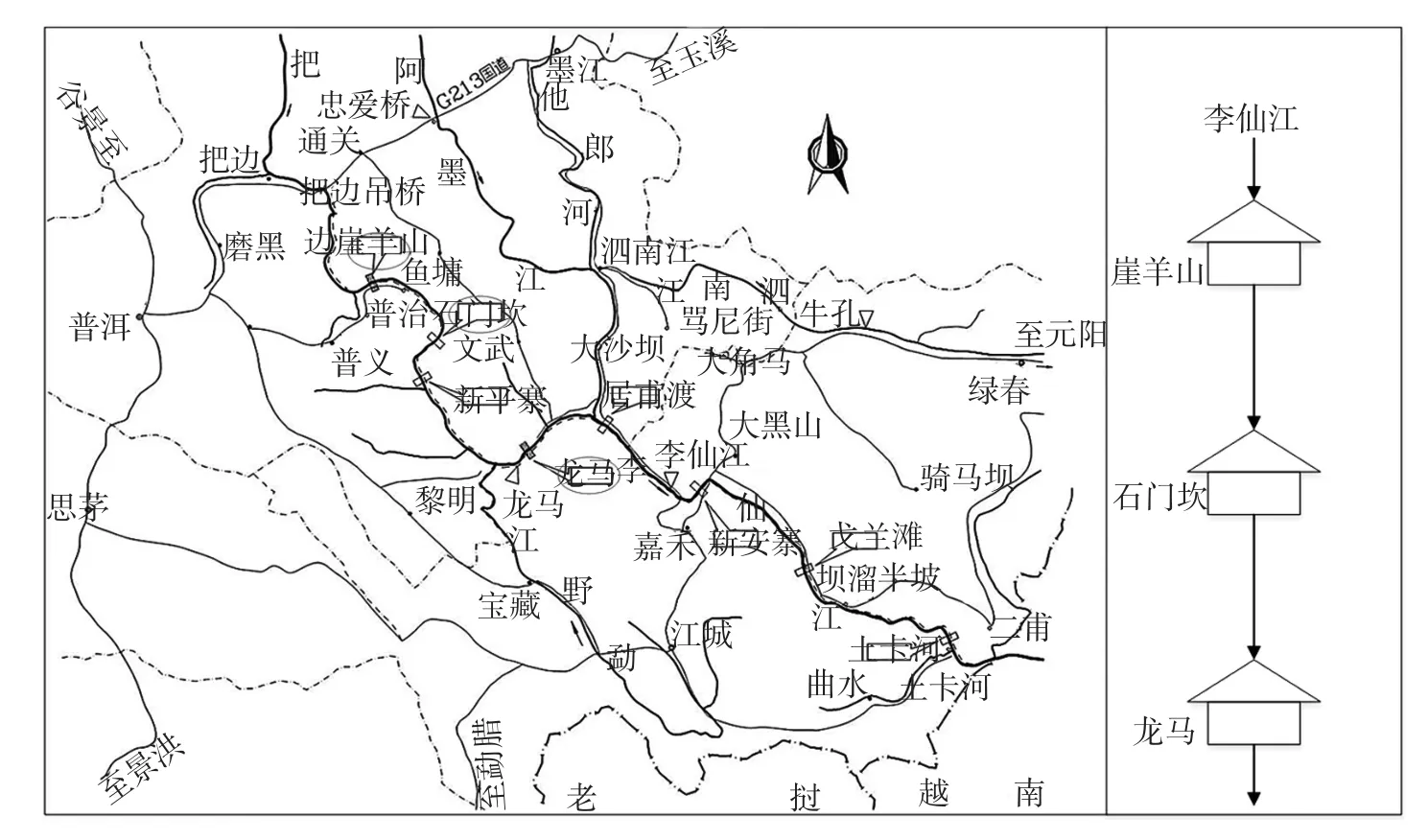
图6　三库联合调度关系

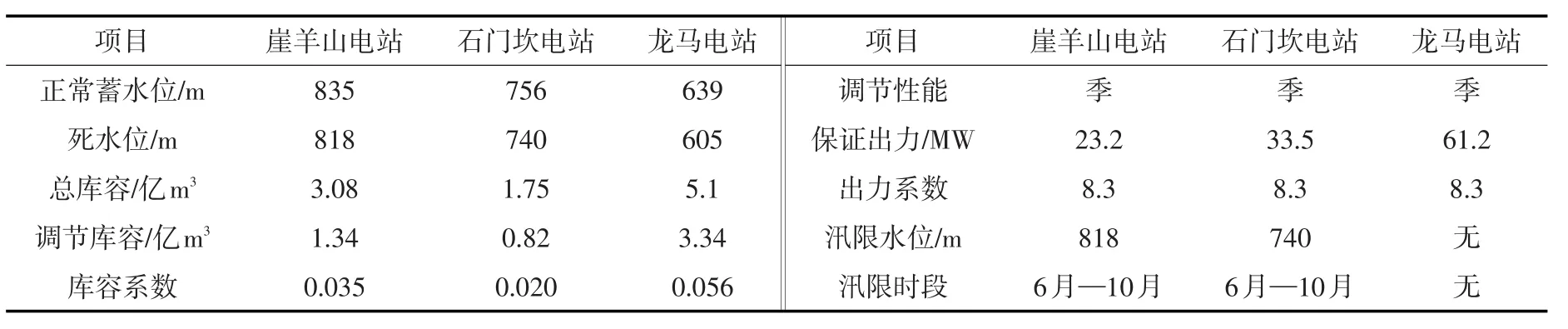
表1　李仙江流域梯级电站基本参数

李仙江流域拥有1957—2000年共43年的长系列径流资料，利用传统动态规划、逐步优化算法（POA）和本文所提出的改进算法对梯级水库实行调度期为1年的优化调度（不考虑水流滞时），选用一典型年径流数据作为计算输入（流量信息如表2所示），比较不同离散数目情况下的计算结果、计算用时等参数，调度期内时段约束如表3所示。

5.1推求可行域搜索映射对三库长达43年的径流资料进行整理统计，得到崖羊山水库的历史最大和最小入库流量分别为613和11.5 m3/s，石门坎水库为692和0.5 m3/s，龙马水库为1042.3和6 m3/s，以0.1 m3/s的离散精度对各库入库流量进行离散，时段初库容按照时段库容约束进行离散，离散数为120，对三库计算不同时段，不同入库流量和时段初库容组合下，时段约束集合耦合转化的时段末库容约束，将结果存储于数据库中。各水库的可行域搜索映射计算完毕后，由于计算所得的映射精度较高，在精度要求低于120个离散点的水库调度问题中，时段可行域可直接通过可行域映射获得，可行域搜索映射无需重复计算。

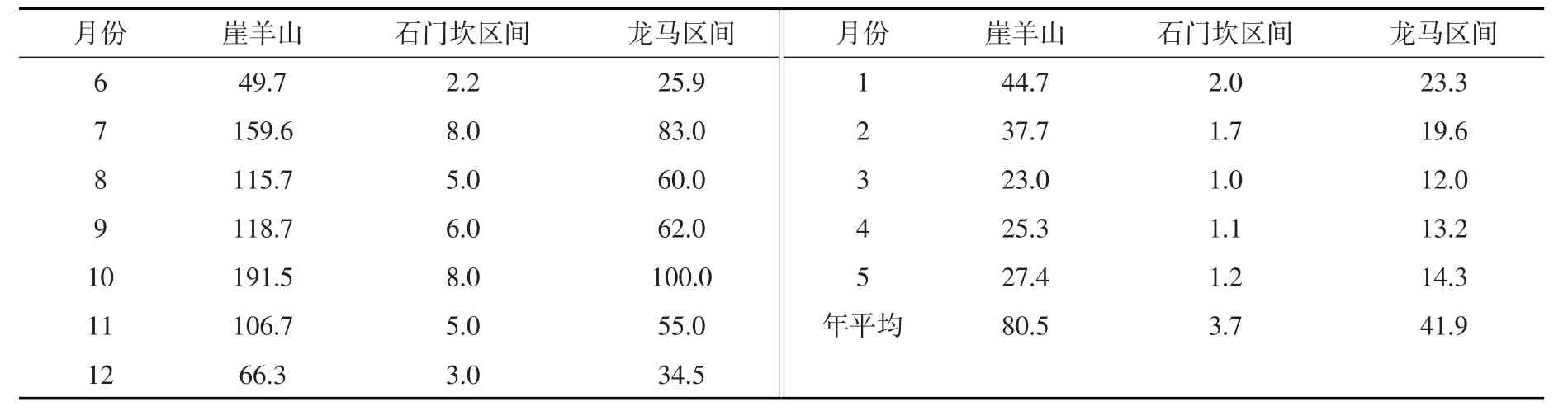
表2　典型年径流数据　（单位：m3/s）

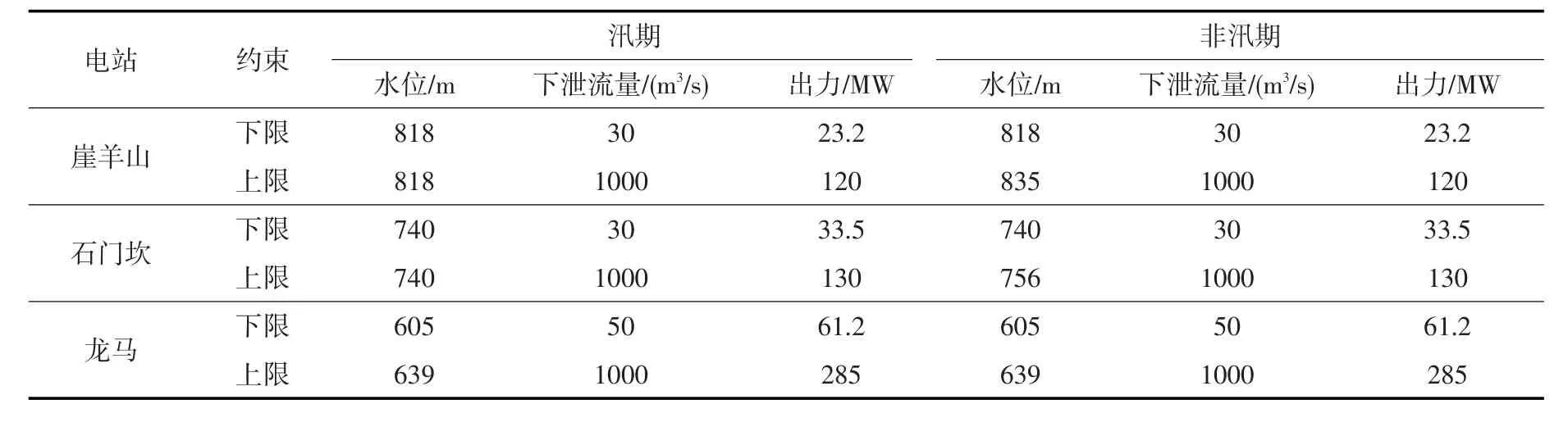
表3　调度期时段约束

图7为7月份三库入库流量为150～180 m3/s情况下的可行域搜索映射曲面图（为便于观察，将库容约束转化为对应的水位约束）。在该入流范围下，单位时段内由正常蓄水位降至死水位的下泄流量不会超过时段下泄流量的约束上限值，故约束下限值曲面为xy轴所在平面，上限值曲面为图7所示曲面，约束上限值曲面和下限值曲面之间为阶段可行搜索区间，以库1为例：当入库流量为175 m3/s，时段初库容离散点为9的条件下，约束上限值曲面与之对应点的z轴值为820.14 m，下限值曲面与之对应点的z轴值为818 m，则该条件下时段末可行搜索区间为［818 m，820.14 m］。由图7可以得出以下几点结论：（1）搜索区间长度随着入库流量的增加而增加，原因是入库流量增加，使得时段内的可调配水量增多，时段约束的本质是与水库相关的各部门对库内存储的水量水能的利益诉求，故当可调配水量增多时，各部门间的利益冲突减缓，搜索区间长度增加；（2）搜索区间长度随着时段初库容离散点的增加而增加，其原因与入库流量增多相同，是时段内可调配水量增多所导致；（3）曲面图具有一定弧度，原因是约束求取过程中所使用的水库特征曲线为非线性曲线，使得搜索区间长度并不随着入库流量或时段初离散点的改变呈线性变化。

5.2改进DP算法的实例应用本文利用5.1节计算出的可行域搜索映射f，对传统DP算法进行改进。传统DP算法由于递推过程中要求对所有库容组合进行遍历，导致计算时间较长，且惩罚因子的选取较为困难，需通过多次试算获得。将f引入递推计算以缩减搜索空间，简化计算流程，从而减少计算时长。并利用时段初循环并行模式，实现传统DP和改进DP的并行化，以充分利用计算机资源，提升计算效率。

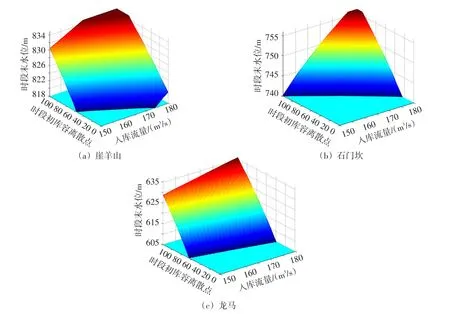
图7　三库可行域搜索映射示意

将李仙江三库组成的梯级水电站系统作为研究实例，以梯级发电量最大为目标建立优化模型，三库调度期初末水位固定，模型的求解分别采用传统DP、并行DP、POA、改进DP和改进并行DP，程序通过Visual C#2010编译工具及其并行拓展库实现，采用的计算平台为联想ThinkCentre M8600t-D066，CPU类型为Inter（R）Core（TM）i7-6700@3.40GHz，内核数为4核，RAM为16.0 GB。选取离散点为20、30、40、60进行计算，不同离散点对应的并行核数均为4核，计算结果如下所示（表4中的速率比是指相同离散点情况下，传统DP与选用的求解方法完成梯级水库优化调度的计算耗时比率）。

从表4的计算结果可以看出，随着离散点数由20增加到60，传统DP的年发电量由18.651亿kW·h增至18.662亿kW·h，保证率由91.67%增至97.22%，而计算规模和耗时大幅增加，计算规模由4.29亿次增至2576.16亿次，计算耗时由4.37 min增至2627.88 min，改进DP的计算结果与传统DP的计算结果相同，说明可行域搜索映射的引入不改变当前离散精度下解的全局收敛性，改进DP相对于传统DP的速率比保持在3.4以上，加速效果等同于采用了4～6核并行计算，随着离散点数的增加，加速比略有下降。而POA的计算规模和耗时虽远小于改进DP，但其计算结果受到初始状态轨迹的影响较大，迭代过程中可能陷入局部最优，无法保证最终结果收敛于全局最优解，相同离散点情况下POA的年发电量与保证率均小于改进DP。从图8可以看出，当离散点为60时，改进DP和POA的水位过程线仍存在较大差异。从表5的计算结果可以看出，采用4核并行计算的并行DP和改进并行DP，随着总计算任务的增加，加速比均逐渐增加，并行效率也不断提高，说明计算任务的增加使得内核的闲置资源得到了充分的利用。其中离散点数从20增加到60时，改进并行DP相对于传统DP的速率比由9.229增至11.007，加速效果十分显著，等同于采用了12～14核并行计算。然而，由于可行域搜索映射将每个阶段内无效库容组合状态剔除，导致并行计算时内核负载不均，故改进DP的并行效率低于传统DP的并行效率，但是在计算耗时方面，随着离散点数由20增至60，并行DP的计算耗时由1.37 min增至759.28 min，而改进并行DP仅由0.47 min增至238.76 min，说明改进并行DP仍具有较大优势。

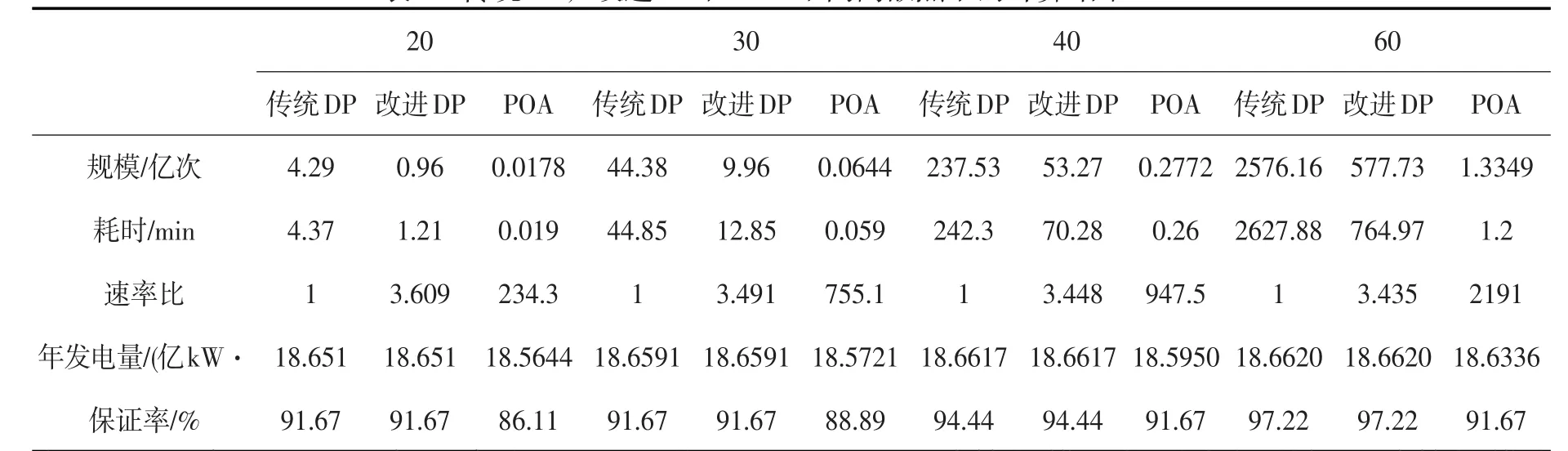
表4　传统DP，改进DP和POA不同离散点下的计算结果

总而言之，可行域搜索映射与并行技术的引入，使得改进算法在求解梯级水电站优化调度问题中既满足了解的全局最优性，又减少了计算时间，提高了计算效率。

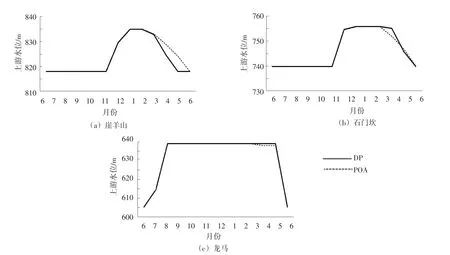
图8　离散点60情况下改进DP与POA水位过程对比

6　结论

本文将映射思想引入水库调度的复杂约束集合处理问题中，提出可行域搜索映射模型，以快速获取阶段可行搜索空间；并在多核环境下，实现算法并行化，提出基于可行域搜索映射的并行动态规划。分别采用传统DP、改进DP算法、POA及相应的并行算法对以李仙江流域三库为研究实例进行了梯级水库优化调度，计算结果表明，基于可行域搜索映射的并行动态规划能在保证年发电量与传统动态规划相同的情况下，减少程序的冗余计算，在全局尺度上实现计算规模的有效压缩，并充分利用计算机多核优势，大幅缩短计算时长。