基于Copula函数的水文随机变量和概率分布计算

宋松柏，王小军

（1.西北农林科技大学 水利与建筑工程学院，旱区农业水土工程教育部重点实验室，陕西 杨凌　712100；2.南京水利科学研究院 水文水资源与水利工程科学国家重点实验室，江苏 南京　210029）

1　研究背景

二维相依水文随机变量和概率分布计算是流域设计洪水地区组成、梯级水库下游设计洪水等的重要内容和核心计算技术。因此，如何提高水文变量和分布的计算精度，受到许多学者的高度关注。《水利水电工程设计洪水计算手册》推荐使用地区组成法、频率组合法和随机模拟法进行设计洪水的地区组成计算［1］。其中，频率组合法推荐使用1990年代王锐琛等提出的概率组合离散求和法。张元禧［2］是我国最早开展二维水文随机变量和概率分布计算的学者之一，推导了具有形状参数为正整数的Gamma水文变量和、差分布解析计算公式。黄农［3］在此基础上，扩充了张元禧的研究结果，提出了两独立Gamma分布变量之和的数值计算方法。21世纪以来，出现了基于JC法、Copula函数以及改进的离散求和法进行梯级水库设计洪水地区组成计算［4-11］。闫宝伟等［6］系统地总结了现有计算方法的不足：离散求和法将二维积分转换为两变量有限个“状态”频率的组合求和，其数据转化过程中难免出现信息失真；随机模拟法通过建立空间多站随机数学模型进行上下游断面及区间洪水过程进行随机模拟，模拟序列统计特征的保持性尚难掌握；地区组成法虽然计算方法简便，但该法将区间洪水按某一组成相对固定，人为因素的不确定性较大。李天元等［7］应用Copula函数，获得条件概率显式表达式，最后对条件概率曲线进行离散来求解二维相依水文随机变量和的分布概率，这种方法提高了概率组合离散求和法的计算精度，无需对变量做独立性处理，但是，它仍然属于概率组合离散求和法。

Nadarajah推导边际分布必须为同一类型分布［12-19］。本文试图根据二维随机变量和分布函数的定义，从二维随机变量和概率分布的定义出发，运用Copula函数和数学积分变换原理，将二维随机变量和概率分布计算转换为条件Copula的一维定积分，力求避免离散求和法数据转化过程中的信息失真。在此基础上，推导了Gamma分布、P-Ⅲ分布两类常用边际分布变量和的分布概率计算公式。以清江流域水布垭水库至隔河岩水库3 h洪量组成为例，说明文中模型的应用。文中模型以期为我国设计洪水地区组成和梯级水库下游设计洪水计算等提供理论支撑。

2　二维随机变量和分布的Copula函数表达式

设二维随机变量(X，Y)的联合密度为f(x，y)，X与Y相互独立，则Z=X+Y的分布概率为［12］：

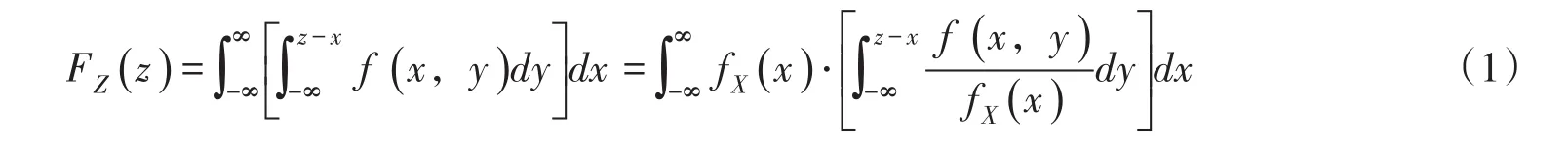
式中：fX(x)为随机变量X的密度函数；随机变量X、Y的积分上、下限可分别根据它们分布函数变量的取值范围来进行确定。

设二维Copula函数为C(u，v)，u=FX(x)，v=FY(y)，其中，FX(x)、FY(y)分别为随机变量X、Y的分布函数。根据Copula函数性质，联合密度f(x，y)与Copula函数C(u，v )有下列关系［21-22］：

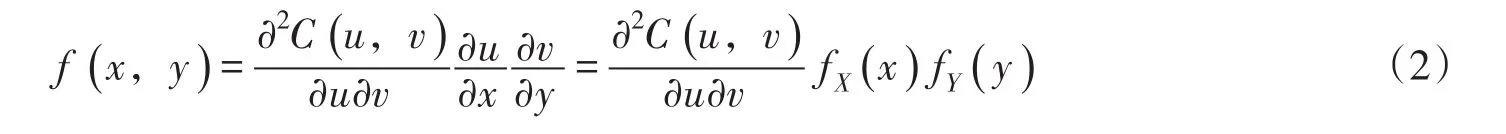
将式（2）代入式（1），有

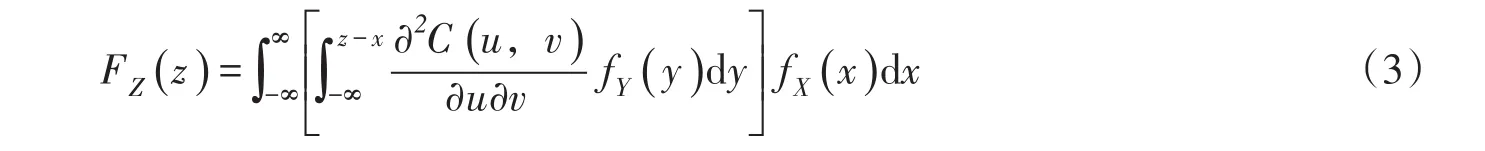
令u=FX(x)，则x=为随机变量X分布的逆函数。当x→-∞时，u=0，当x→∞时，u=1，du=dFX(x)=fX(x)dx；v=FY(y)，当y→-∞时，v=0，当v=z-x时，v=FY(z-x)=FYdv=dFY(y)=fY(y)dy，则

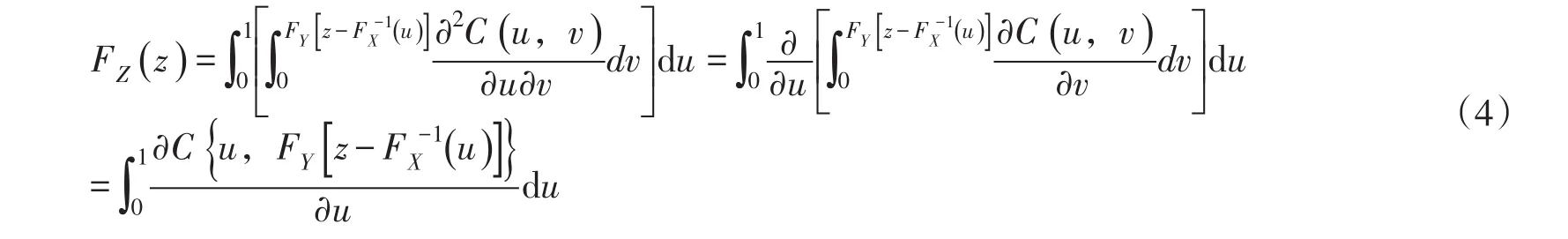
式（4）即为二维随机变量和概率分布的Copula函数计算表达式，显然，积分函数仅为变量u的函数。二维Copula函数为C(u，v)可根据二维随机变量(X，Y)的相依特性，按照通常基于Copula函数的多变量分布计算方法选择函数类型和确定相应的参数。积分变量u的上、下限可根据随机变量X的取值范围，通过u=FX(x)来进行确定。

3　边际分布Gamma、P-Ⅲ分布下变量和分布Copula函数表达式

Gamma、P-Ⅲ分布是水文中常用的分布函数，以下将根据式（4）推导边际分布服从Gamma、P-Ⅲ分布的变量和分布Copula函数表达式。

假定随机变量X和Y服从Gamma分布，其密度函数分别为

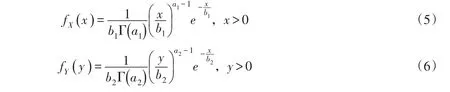
若随机变量X和Y服从P-Ⅲ分布，则其密度函数分别为：

式中：a1、a2分别为形状参数；b1、b2分别为尺度参数；c1、c2分别为位置参数；

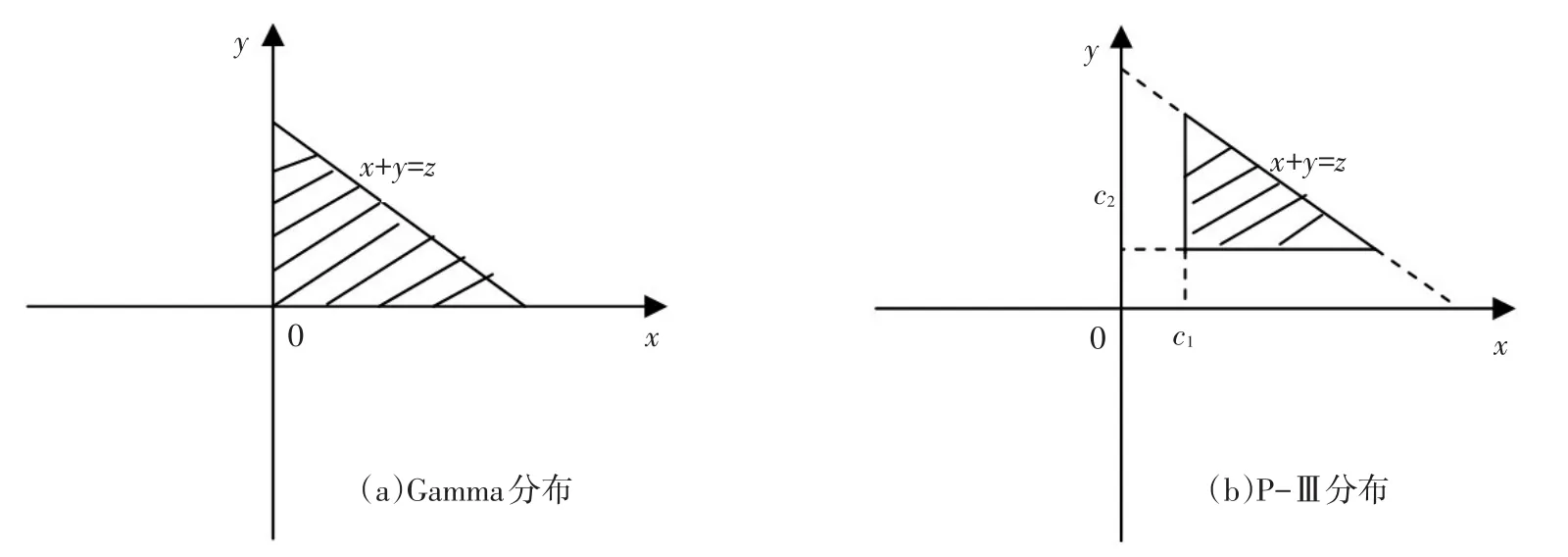
图1　积分区域

给定Gamma、P-Ⅲ边际分布下，变量和分布Z=X+Y概率计算的积分区域见图1所示。Gamma分布变量X和Y分别取值x＞0，y＞0，P-Ⅲ分布变量x＞c1，y＞c2，z=x+y为有限值，且已知，根据图1所示的积分区域和二维定积分原理，x积分则转换为变量u积分，其上限值为z的x边际分布值，不再取值1。

式中，对于边际分布服从Gamma分布，u=FX(x)=d t，v=FY(y)d t；对于边际分布服从P-Ⅲ分布，u=FX(x)=v=FY(y)

4　二维随机变量和概率分布模型求解

由式（9）可以看出，z已知，二维随机变量和概率分布FZ(z)仅为变量u的一维定积分。当函数为简单初等函数时，可获得FZ(z)的解析积分值。实际中，Copula函数表达式一般较为复杂，形式复杂，只能采用数值积分获得FZ(z)的数值积分值。本文采用连分式数值积分法计算FZ(z)，其步骤如下［23-24］：

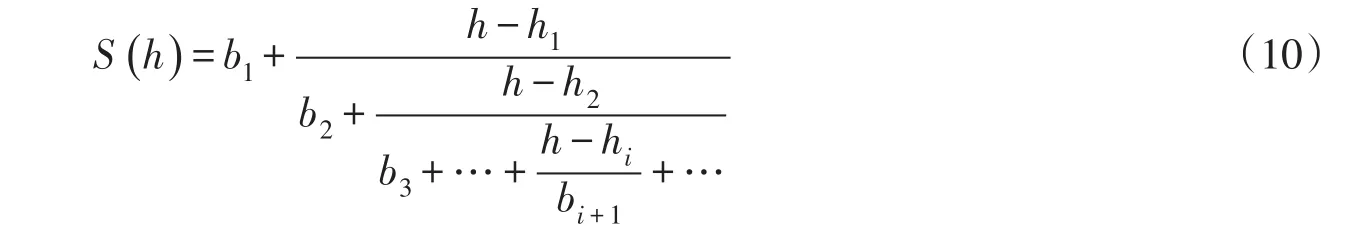
式中，b1，b2，…，bi，…，由式（11）计算的一系列积分近似点(hi，Si)来确定，i=1，2，…。

当h=0时，S(0)即为积分值。即

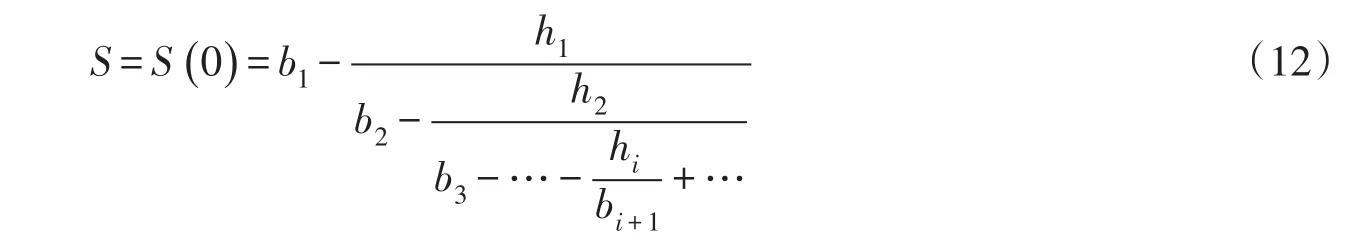
实际计算中，连分式计算一般取i=7-10就能满足精度要求。

5　应用实例

本文选用文献［7］采用的清江流域梯级水库3 h洪量序列分布参数和Copula函数参数，说明二维相依水文随机变量和概率分布计算模型的应用。X代表水布垭水库3 h洪量，Y代表水布垭水库至隔河岩水库区间（水-隔区间）3 h洪量，水布垭水库水量加上水-隔区间水量等于下游隔河岩水库水量。3种序列的统计参数和分布参数见表1［7］。

表1　序列参数计算结果

选用二维Gumbel-Hougaard Copula函数，其分布函数为：

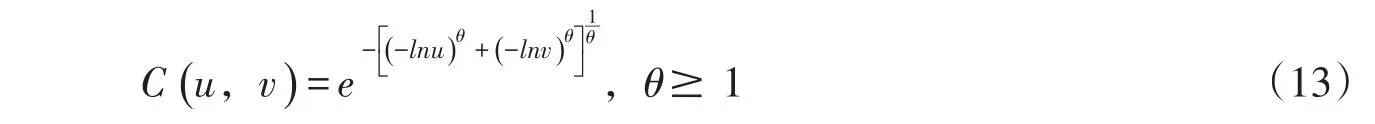
式中：u=FX(x)、v=FY(y)分别为边际分布，θ为Gumbel-Hougaard Copula函数参数，本文中θ=1.89。根据式（13），有Copula函数的偏导数：

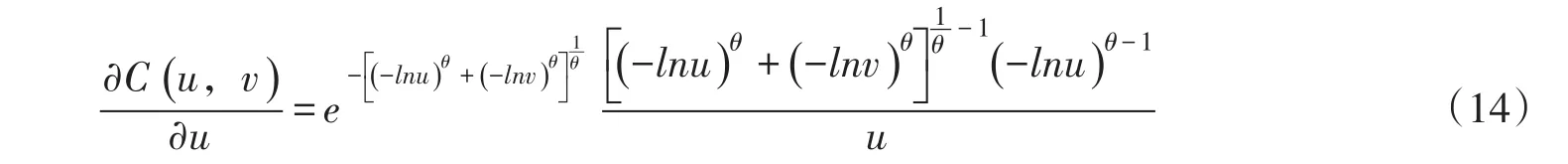
将式（14）代入式（9），随机变量X和Y分别选用Gamma、P-Ⅲ分布，应用上述连分式数值计算方法，两种边际分布下，X+Y≤Z的概率计算结果分别见表2第（2）和第（5）列，其对比见图2所示。为了验证文中模型计算结果的正确性，表2第（3）和第（6）列分别列出X+Y序列分别按Gamma、P-Ⅲ分布计算的理论概率值，第（4）和第（7）列给出了相应的误差计算值。其误差是由于X、Y分布参数不同，式（4）没有显式解析计算公式，只能由文中变步长梯形法数值计算，因而具有一定的偏差，另外也受边际分布拟合精度的影响。不难看出，两种边际分布下，文中模型与变量和序列的和概率分布计算结果基本一致，表明文中模型和计算方法是正确的。

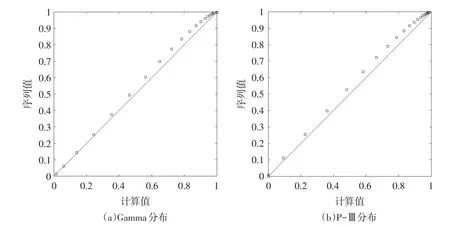
图2　X+Y≤Z分布概率计算结果对比

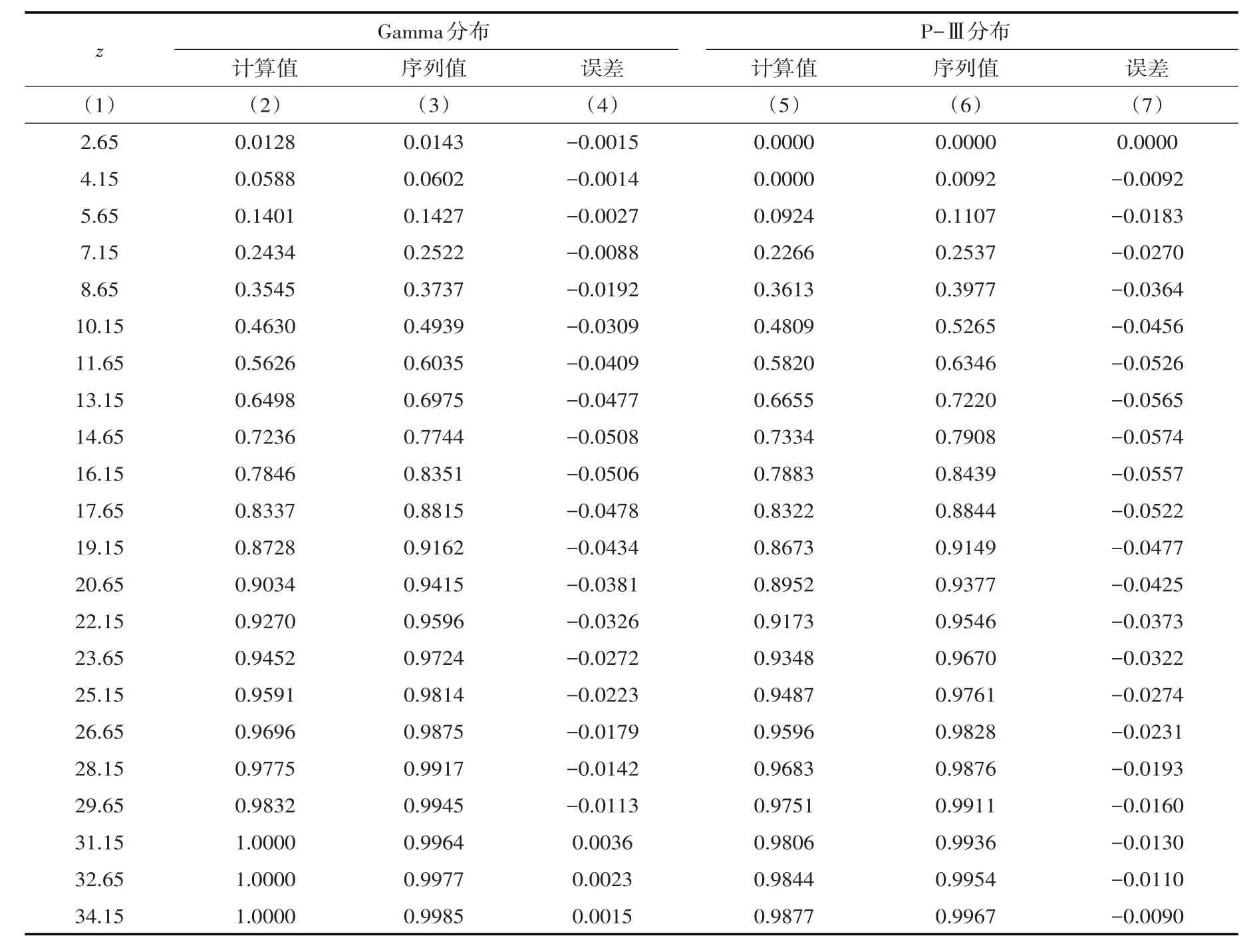
表2　X+Y≤Z分布概率计算结果

6　结论

二维相依水文随机变量和概率分布计算是梯级水库下游设计洪水计算、设计洪水地区组成的重要计算内容。本文基于Copula函数和数学积分变换原理，严格地推导了两Gamma分布、P-Ⅲ分布相依水文随机变量和分布的概率计算公式。以清江流域水布垭水库至隔河岩水库3 h洪量组成为例，说明文中模型的应用。主要研究结论如下：（1）文中计算公式克服了离散求和法进行数据转换中可能出现的误差。（2）计算公式表达为一维条件Copula函数的定积分，利用计算机数值积分，不难获得满意的求解结果。对于P-Ⅲ分布，通过计算序列变量值减去分布的位置参数，即可转换为Gamma分布函数值计算。（3）文中二维相依水文随机变量和概率分布采用条件Copula函数计算，可方便地组合不同分布相依的水文特征变量，可克服传统多变量分布函数要求同一类边际分布函数的限制。（4）研究区两Gamma分布、P-Ⅲ分布下，洪量组合和概率分布结果表明，文中随机变量和概率分布计算公式是正确的。文中模型以期为我国流域设计洪水地区组成和梯级水库下游设计洪水计算提供理论支撑。（5）文中仅根据下游设计断面洪量等于上游水库断面洪量和区间洪量之和，没有考虑水库的调节影响，推导了下游设计断面洪量概率分布计算公式。因此，如何考虑水库调洪影响下的下游断面设计洪水有待于进一步深入研究。