赣江流域洪水峰量演变规律及联合分布研究
2022-08-04袁鹏飞郭红虎韩会明吴宇飞
袁鹏飞,郭红虎,韩会明,吴宇飞
(1. 江西省赣州市河湖保护中心,江西 赣州,341001;2. 江西省水利科学院,江西 南昌,330029)
0 引 言
气候变化影响下,流域洪水情势发生变化,洪水特征的变化对防洪、水库管理、生态系统等产生重大影响[1,2]。因此,评估洪水事件的特征,以便采取适当的适应策略具有重要意义。洪水具有多属性特征,如洪峰和洪量,单变量频率分析无法描述洪水事件发生的概率[3,4],开展多变量洪水频率分析对于更好地理解洪水的特征至关重要。Copula 函数具有灵活多样的特点,其在构建多变量联合分布时对边缘分布函数的类型没有限制,在水文事件的分析中得到广泛的应用[5-7]。赣江是鄱阳湖流域最大的支流,其入湖洪水峰量分析对湖区防洪具有重要意义,因此,本文依据赣江控制水文站—外洲站实测年最大洪峰流量和1 日洪量,利用Copula 函数对其洪水峰量特征进行联合分析。
1 研究区概况及数据方法
1.1 研究区概况
赣江流域属于亚热带湿润季风气候,年平均气温为17.8℃,最高温度为39.5℃,最低温度为-5.8℃,流域面积约为8.28 万km2,干流全长约823km,发源于江西省西南部,汇入鄱阳湖,最后流入长江。赣江是流入鄱阳湖的五条河流中最主要的支流,对鄱阳湖的生态环境起着至关重要的作用。
1.2 数据来源
赣江流域控制水文站—外洲站的1950~2019 年共70 年的逐日流量资料来源于江西省水文监测中心,统计筛选出年最大洪峰流量和最大1 日洪量,分析洪水峰量演变规律,并使用Copula 函数进行联合分析。
1.3 研究方法
构建联合分布之前,先对洪水洪峰和洪量进行边缘分布函数拟合和相关性分析,本文分别使用对数正态分布(LN)、指数分布(EXP)、伽玛分布(GAM)、广义极值分布(GEV)、威布尔分布(WBL)和P-Ⅲ型分布对洪水洪峰和洪量进行拟合,通过Kolmogorov-Smirnov 检验洪峰和洪量的边缘分布函数拟合效果,并通过Kendall、Spearman、Pearson 三种相关系数方法度量洪峰和洪量之间的相关性,最优使用Gumbel copula、Clayton copula 和Frank copula 函数构建联合分布函数,并通过平方欧氏距离(d2)和赤司信息量准则法(AIC 方法)筛选出最优拟合的Copula 函数,最后进行联合重现期的分析[8,9]。

式中:洪峰洪量边缘分布分别为Fx(x)和Fy(y),F(x,y)为二维联合分布函数。
此外,文中使用了常用的水文数据检验方法—Mann-Kendall 检验,具体原理及公式可参考文献[8]。
2 结果分析
2.1 洪水峰量年际变化
赣江流域年最大洪峰均值为11 832.6m3/s,最大洪峰发生在2010 年,为21 500m3/s,最大1 日洪量均值为9.99×108m3,最大洪量发生在1982 年,为17.37×108m3。图1 为赣江流域最大洪峰和最大1 日洪量年际变化过程图。从图1 可知,赣江洪峰和洪量整体上均呈现出减小的趋势,洪峰和洪量在各年代间均保持着升降一致,1950 年代-1960 年代增加,1970 年代回落,之后的1980 年代和1990 年代持续增加,2000 年代出现明显地减少,在2010 年代又有所上升。利用Mann-Kendall检验结果表明,洪峰和洪量减少趋势并不明显,同时突变分析结果如图2 所示,洪峰和洪量在1970-1990 年代期间UF 和UB 曲线多次相交,但均未超过0.05 显著性水平,并无明显突变。
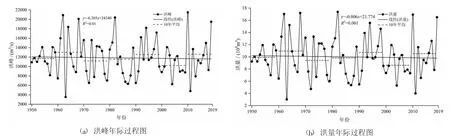
图1 洪峰和洪量年际过程图
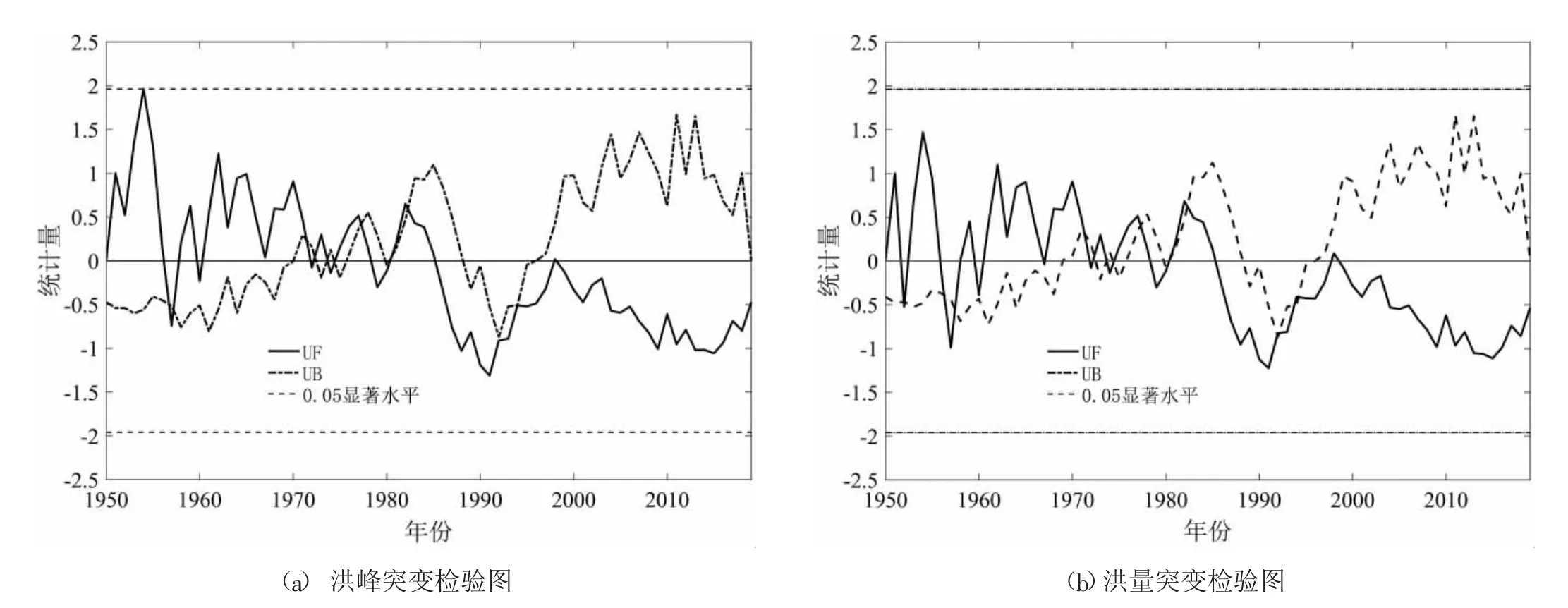
图2 洪峰和洪量突变检验图
2.2 洪水峰量联合分布研究
2.2.1 边缘分布函数拟合及其相关性
通过最优边缘分布函数拟合效果,检验结果表明,洪峰和洪量的最优分布均为gamma 分布函数,K-S 检验统计值分别为0.046 5 和0.043 4,显著水平0.05 对应的临界值为0.159 8,通过检验。绘制最优边缘分布的理论频率与经验频率拟合效果q-q 图3。从q-q 图可以看出,点据集中分布于45°线附近波动,所以洪峰和洪量对应的边缘分布函数拟合的分布函数效果良好。洪峰和洪量的相关性度量结果为,Kendall 相关系数为0.981 7,Spearman 相关系数为0.998 8,pearson相关系数为0.997 7,表明洪峰和洪量之间存在强相关关系。

图3 洪峰、洪量拟合效果q-q 图
2.2.2 Copula 函数拟合优选
采 用Gumbel-copula、Clayton-copula 和Frankcopula 三种Copula 函数建立洪水峰量的联合分布,分别用平方欧氏距离(d2)和赤司信息量准则法(AIC)评定各种Copula 函数拟合结果。结果表明:赣江年最大洪峰和1 日洪量适合运用Frank-copula 进行洪水峰量特征分析(见表1)。

表1 Copula 函数拟合优选
2.2.3 洪水峰量重现期分析
表2 为不同边缘分布重现期下,对应的洪峰和洪量设计值及联合重现期。从表2 可知,边缘分布重现期介于联合重现期和同现重现期之间,且随着边缘分布重现期的增加,同现重现期与联合重现期之间的差距逐渐增大。联合重现期和同现重现期可看作是边缘分布的两种极端情况,因此,可以根据联合分布的重现期估计实际重现期的区间。当单变量重现期为5 年一遇时,设计洪峰为15 009m3/s,洪量为12.683×108m3,其实际重现期为4.89~5.12 年;当单变量重现期为100 年一遇时,设计洪峰为23 093m3/s,洪量为19.529×108m3,其实际重现期为72.51~161.05 年。
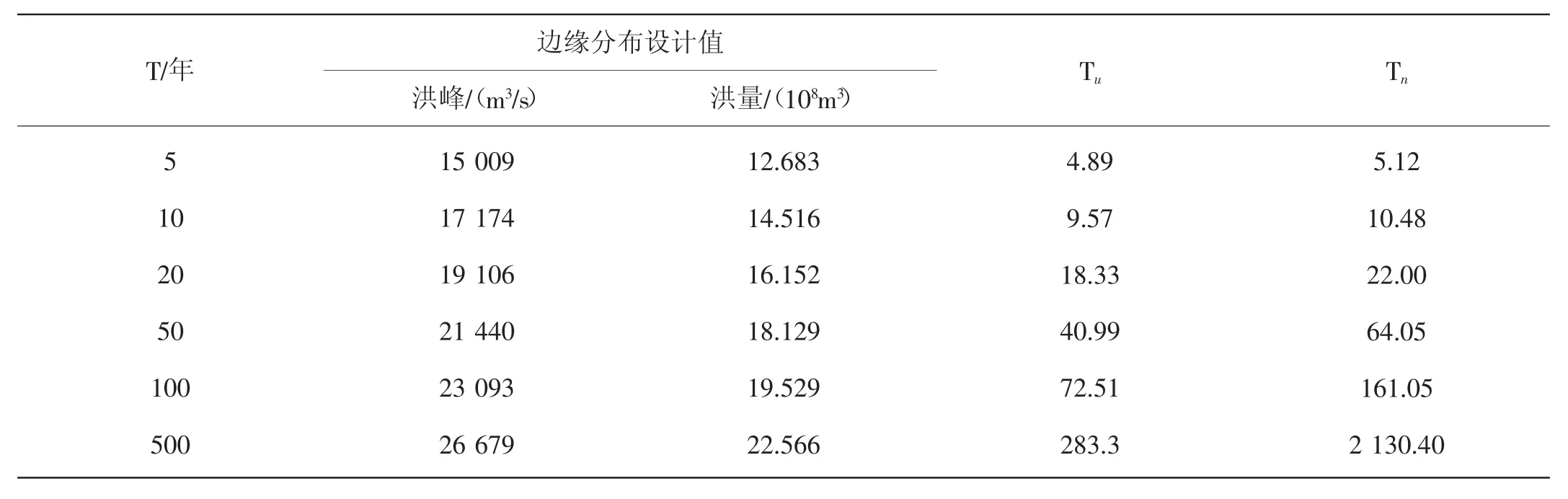
表2 单变量设计值与峰量联合分布重现期
3 结 论
(1)根据洪水峰量的年际趋势变化分析,峰量均呈现减少的趋势,70 年间洪水峰量呈现出升降—升降—升的变化过程。
(2)赣江洪峰和洪量呈现出良好的相关关系,并且两者均服从gamma 分布。
(3)利用Frank copula 函数建立洪峰和洪量的二维联合分布,分析不同洪峰洪量条件下的联合重现期和同现重现期,其中洪水单变量重现期为5 年一遇时,实际重现期为4.89~5.12 年;当单变量重现期为100 年一遇时,实际重现期为72.51~161.05 年。
