悬移质泥沙输移扩散方程适用条件的讨论

张　磊，关见朝，王友胜，胡智丹，王协康

（1.中国水利水电科学研究院，流域水循环模拟与调控国家重点实验室，北京　100048；2.水利部水文局，北京　100053；3.四川大学 水力学与山区河流开发保护国家重点实验室，四川 成都　610065）

1　研究背景

悬移质泥沙颗粒具有相对较小的颗粒粒径和较大的比表面积，具有更强的吸附能力，因而与水质变化、有机污染物等的输移扩散密切相关，是影响水环境、水生态的重要因素之一［1-3］。因此，研究悬移质泥沙的输移扩散规律具有重要的科学价值。

针对悬移质输移过程中的泥沙浓度分布，众多学者基于不同理论提出了不同的研究方法。从最初基于紊流扩散理论的传统扩散方程—Rouse公式［4］以及后续对Rouse公式不同类型的修正式［5-11］，发展到利用两相流理论建立的泥沙扩散模型［12-13］，使我们对泥沙悬浮规律有了基本的认识。近年来，随着泥沙动理学理论的发展，利用动理学理论对悬移质泥沙扩散开展了深入的研究，进一步探究了泥沙悬浮背后隐藏的力学机理［14-19］。概括来说，虽然各家理论的出发点有所不同，但最终的公式形式均与传统泥沙扩散方程类似。由于各家公式在推导过程中采用了不同的假设条件，以致公式在实际工程应用中受到了不同的限制。因此，在公式应用之前需要明确不同扩散理论的适用范围，以免将理论本身的问题与其他现象相混淆，这也有利于我们进一步发现现象背后隐藏的力学机理。

基于此，本文通过对比分析各家扩散方程之间的异同点，明确了不同扩散模型的适用条件以及影响悬移质泥沙输移的关键因素，可为实际工程应用提供参考。

2　悬移质泥沙的扩散方程

2.1传统扩散模型

2.1.1Rouse公式在河流动力学和泥沙运动的经典论著中，通常将泥沙颗粒的悬浮归结于明渠湍流的紊动扩散作用［3］。若重力的沉降作用完全被湍流的紊动扩散作用所抵消时，可得Rouse公式［4］：

式中：ωs为泥沙颗粒的沉速；为悬移质泥沙浓度；εp为泥沙颗粒在湍流中的紊动扩散系数（即泥沙扩散系数）；y为垂向坐标。

根据式（1）便可以得到悬移质泥沙浓度的垂线分布规律。Rouse公式能够描述明渠湍流中泥沙颗粒受到的最主要作用力，但是在很多情况下Rouse公式并不能总是很好地反映实际情况［16，18-19］，其原因包括以下两点：（1）Rouse公式推导过程中的一个重要假定是：仅在垂直方向上泥沙颗粒与水流存在速度差，其值等于泥沙颗粒的沉速。该假定反映的物理本质是对泥沙颗粒的受力分析过程中，仅仅考虑了重力沉降作用，颗粒碰撞力、颗粒惯性以及其他应力等作用均未作考虑；（2）假定泥沙扩散系数与水流动量紊动扩散系数相等。事实上，实际情况中很难满足上述假定。由于Rouse公式存在的上述问题，导致其计算结果在浓度较高、或颗粒惯性较大时计算值与观测值无法吻合。

2.1.2Rouse扩散方程的修正鉴于Rouse公式存在的问题，后续诸多学者从不同角度对其进行了修正和完善［5-11］。下面将对其代表性成果进行简述。

（1）对水沙两相守恒的修正。Hunt［5］在Rouse公式的基础上，考虑了水沙两相的质量守恒关系，得到了式（1）的修正式：

后续张小峰等［8］在Hunt公式的基础上进一步考虑了泥沙颗粒表面吸附水效应的影响。该修正由于考虑了水沙两相的质量守恒关系，使其能够满足浑水连续性假定，而Rouse公式由于不满足该假定，使得在高浓度条件下的计算误差可能较为显著，因此，该修正具有重要的价值。但是，由于Hunt公式尚未涉及对Rouse公式两大基本假定的修正，因此，Hunt公式的适用条件仍然受到了很大限制，仅仅适用于低浓度、细颗粒条件。

（2）对泥沙扩散系数的修正。Rouse公式的重要假定之一是泥沙扩散系数与水流动量紊动扩散系数相等。为了修正该假设带来的误差，学者们采用了以下两种思路。其一，张瑞瑾［10］、张红武［11］等人在确定水流动量紊动扩散系数时采用了不同形式的流速公式，进而解决了Rouse公式水面含沙量为零和底部含沙量无穷大的问题。其二，在水流动量紊动扩散系数的基础上乘以参数β。Vanoni［6］、Van Rijn［7］、Coleman［8］等人根据试验资料给出了参数 β的经验性公式。概括来说，β的大小与泥沙浓度、颗粒粒径、水深等因素有关，目前尚无统一、明确的理论公式。在具体应用中通常是根据实测资料对参数β进行调整使得Rouse公式计算值与实测值相吻合，因此，其适用范围受到实测资料的较大限制。后续Ni［14］提出了统一公式，基本涵盖了各类修正Rouse公式，为分析各类修正间的相互关系提供了理论基础，深化了对Rouse公式特性的认识。

尽管Rouse公式在实际应用中仍然存在不少问题，但不可否认的是，Rouse公式是泥沙运动力学中最重要的经典理论成果之一，是研究泥沙输移的重要理论基础，也是后续开展相关理论研究的重要参考标尺。

2.2两相扩散模型考虑到传统扩散方程存在的上述问题，学者们尝试运用其他理论来研究泥沙的悬浮和输移问题。挟沙水流作为典型的两相流运动，近年来，两相流理论被广泛应用于泥沙输移的研究中，取得了丰硕的研究成果。刘大有［20］基于两相流的双流体模型分析了传统扩散方程存在的不足。由于两相流理论的控制方程是固液两相的质量和动量守恒方程，通过求解得到的挟沙水流宏观变量变化规律可以反映水沙动力学特性对泥沙输移的影响，这也是两相流理论最大的优势。下面对基于两相流理论的悬移质扩散方程的代表性成果进行简要介绍。

2.2.1Cao扩散模型Cao［12］基于两相流的基本控制方程，同时对脉动速度与浓度关联项采用了与Rouse公式一样的封闭方法，得到了悬移质的扩散方程为：

将式（4）代入式（3）可得：

由式（5）可以看出，Cao修正模型中通过两相流的质量加权出现了这样的修正项。但本质上并没有解决Rouse公式存在的问题和应用上的局限性。泥沙扩散系数依然是借用经验公式来确定，即：

式中νt为紊动涡黏性系数。在Cao的计算过程中根据实验数据确定参数 β，在机理上并没有很好地揭示悬移质的运动机理。

2.2.2Wu和Wang的两相扩散模型Wu和Wang［13］基于两相流的双流体模型提出了悬移质输移的两相扩散模型。模型的关键参数是固液两相间的相对速度差。为了确定该参数，建立了相间速度差的控制方程，这也使该模型更具有普适性。但是，由于相间速度差的控制方程的求解较为困难，为了能够得到其理论表达式，在求解过程中忽略了颗粒惯性高阶项的影响，得到的相间速度差表达式为：

由于模型中对瞬时输沙方程进行了雷诺平均，因此产生了紊动浓度高阶项，反映了泥沙紊动带来的影响，该项在泥沙浓度较高时影响较为显著。与Cao扩散模型相比，Wu和Wang两相扩散模型不仅满足了浑水连续性条件，同时能够体现泥沙紊动的影响。但是，泥沙紊动项尚未给出相应的封闭方程，实际中难以计算该项。另外，由于求解过程中忽略了颗粒惯性的影响，因此该模型在大颗粒惯性条件下受到了较大限制。

2.2.3Ishii和Hibiki的漂移-通量模型Ishii和Hibiki［21］提出的漂移-通量模型中，其研究对象是水沙混合物，虽然其控制方程形式与两相双流体模型类似，但其推导过程并非严格由双流体模型而来。因此，在实际应用中需要给出相应的封闭条件，其关键参数—两相间速度差，具体表达式为：

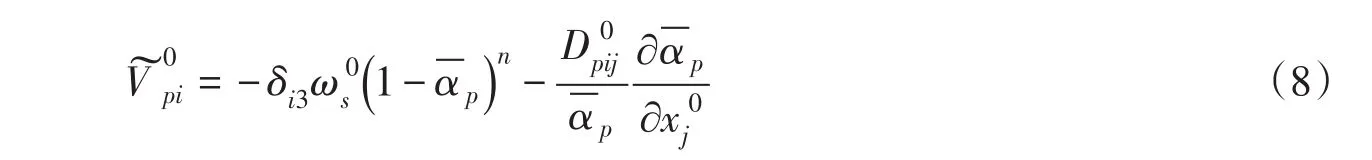
2.2.4Snehasis Kundul和Koeli Ghoshal基于漂移速度的扩散模型近期Snehasis Kundu1和Koeli Ghoshal［22］基于两相流的固相动量守恒方程建立了悬移质扩散模型，在该模型中的重要参数-漂移速度，采用的是Gerimann［23-24］及Zhong等［18］文献中给出的漂移速度表达式，即：

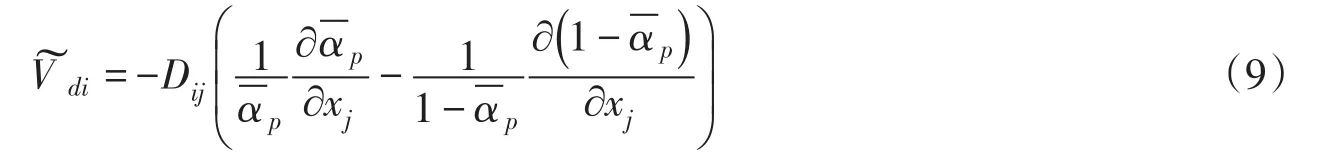
其中Dij为扩散系数张量。据此式得到的扩散方程为［22］：

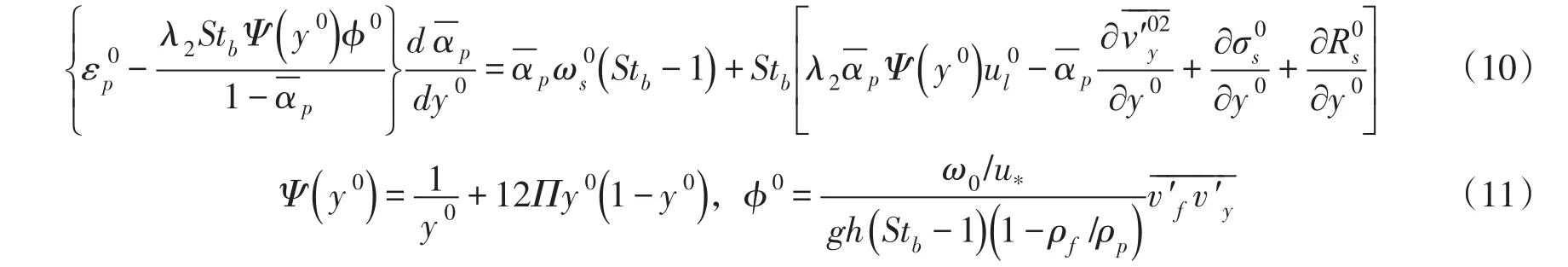
泥沙扩散系数εp由下面的经验公式决定：

式中：γ为系数，根据不同实验资料进行率定；颗粒Stokes数Stb=-τpu*/h，反映了泥沙颗粒弛豫时间与水流特征时间尺度之比；λ2为升力系数；ul为两相速度差；v′y为颗粒垂向脉动速度；σs为颗粒之间的应力大小；Rs为雷诺应力；Π为尾流系数。

从式（10）可以看出，该模型中包含了颗粒惯性、升力、拖曳力、颗粒间相互作用等因素对悬移质扩散的影响。通过与多家实测资料对比论证了该模型的适用范围较广，能够反映悬移质Ⅰ型分布和Ⅱ型分布的变化，并指出了影响分布类型的关键参数是颗粒Stokes数。随着Stokes数的增大，悬移质分布形式逐渐由Ⅰ型变为Ⅱ型。但该模型中，在计算液相流速分布时，采用的仍然是传统的对数-尾流公式，而不是由双流体模型直接计算液相速度，因此，随着泥沙浓度的变化，尾流函数如何确定，目前尚未形成统一的认识，理论上有待进一步完善。另外，从式（12）可以看出，在确定泥沙扩散系数上仍然采用的是类似于β系数的经验公式，因此在应用上会同样会受到实验资料的限制。

2.3基于动理学理论的扩散模型除了两相流理论外，Ni等［14］、傅旭东等［15］、Fu等［16］、范念念等［17］、钟德钰等［18-19］利用动理学理论对悬移质泥沙浓度分布、泥沙悬浮机理等问题开展了研究，加深了对泥沙输移特性和运动机理的认识。基于颗粒速度分布函数及其演化方程建立的动理学理论，其最大优势之一在于该理论具有把颗粒动力学属性嵌入到宏观统计规律和输沙特性的能力［25］，因此能够在泥沙输移宏观属性中准确反映颗粒动力学特性的影响。下面对在动理学理论框架下建立的悬移质泥沙扩散方程进行简要介绍。

2.3.1基于PDF输运方程得到的扩散方程傅旭东等［15］基于单颗粒Lagrange方程的PDF输运方程对悬移质泥沙浓度分布开展了研究，得到的悬移质泥沙浓度分布方程为：

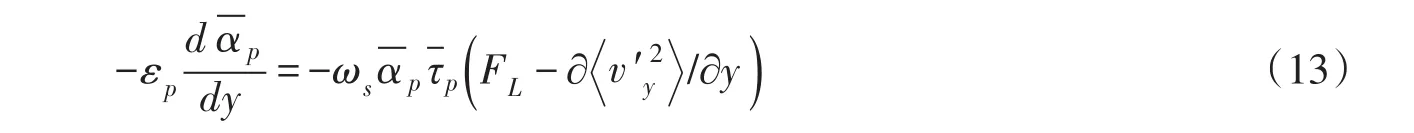
式中：泥沙颗粒扩散系数ε包括两部分，即颗粒无规则脉动和水流紊动扩散；为颗粒弛豫时间，

p反映颗粒惯性的影响；FL为综合升力，包括Saffman力、Magnus力等。式（13）中，等式右边第一项体现了重力沉降作用，第二项反映了颗粒相脉动强度梯度和升力所产生的垂向合力以及颗粒惯性对泥沙扩散的影响。相应的 β参数的表达式为：

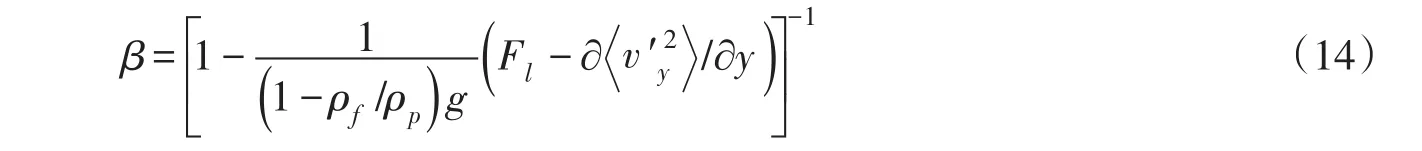
为与后续弥散方程相比，引入摩阻流速u*和水深h作为速度尺度和长度尺度，式（14）变为：

从式（15）可以看出，参数 β并不是一个常数。因此，在对Rouse公式进行修正时取参数 β为常数的做法存在缺陷。另外，升力和颗粒相脉动强度梯度对 β的影响受到颗粒惯性大小的直接制约，当颗粒惯性较小时，即stb趋于0时，可以忽略二者的影响，但随着颗粒惯性的增大，这两种机制对 β的影响也随之增强。与传统的Rouse、Hunt等扩散方程相比，该方程能够更好的阐释悬移质泥沙颗粒的运动机理。在此基础上，作者结合Lyn（1988）、Coleman（1986）以及Wang&Qian（1989）的试验资料对细颗粒、低浓度条件下的浓度分布做了计算分析，进一步研究了传统泥沙扩散方程存在的概念性误差［15］。结果表明，基于PDF方程的泥沙扩散模型由于考虑了升力、颗粒相脉动强度梯度等作用，合理描述了悬移质泥沙的扩散特性，给出了泥沙扩散系数的显式表达式，结合实验资料重点分析了细颗粒条件下两种作用机制对泥沙扩散的影响。得到的参数 β理论表达式（15）中虽然反映了颗粒惯性一阶项的影响，但由于细颗粒条件下颗粒惯性较小，所以作者并没有对此开展专门的研究。

2.3.2悬移质泥沙弥散方程除上述基于PDF方程得到的扩散方程外，近期，Zhong等［18-19］、钟德钰等［25］从以统计力学为基础的（介观）动理学方程出发，推导了宏观守恒方程。在此基础上，引入弥散速度的概念，进而建立了挟沙水流的弥散模型。与两相流理论相比，推导得到的宏观守恒方程在形式上与两相流理论的控制方程是完全一致的，但是由于在推导过程中包含了物理量微观动力学特性变化的影响，因此，得到的守恒方程能够揭示挟沙水流宏观特性变化规律与微观动力学特征之间的本质联系［25］。

弥散速度定义为水中各分相与浑水之间的相对速度差。考虑到明渠挟沙水流中泥沙颗粒的Stokes数是一个小量，因此，采用摄动法通过求解固相动量方程得到了弥散速度的渐近解，即：

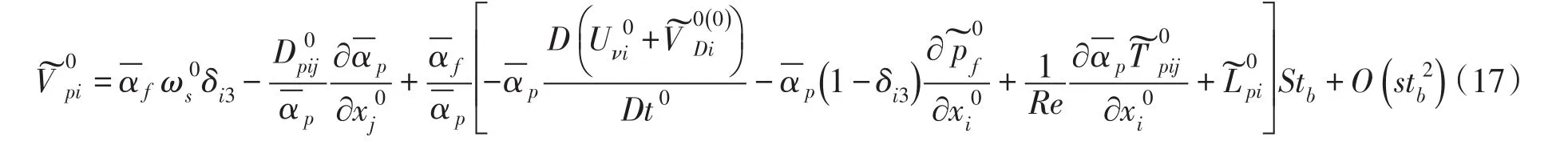
式（17）即为弥散速度的本构关系。式中体现了影响泥沙颗粒弥散速度的多种因素，包括Stokes数零阶项中的重力和浑水紊动扩散作用以及Stokes数一阶项中的流体惯性、颗粒紊动和颗粒间相互作用等。基于上述弥散速度的本构关系，对于恒定均匀流，悬移质泥沙的弥散方程为［18］：

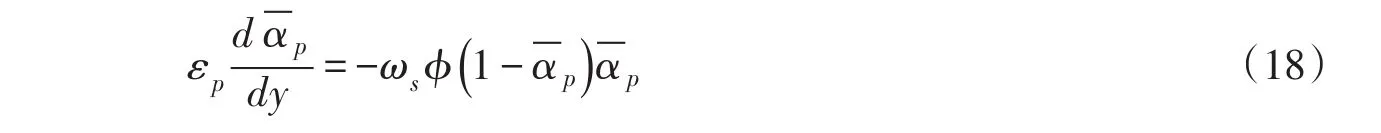
其中泥沙扩散系数εp和参数φ的表达式为：

和

对式（18）进行无量纲化和适当变形，可以得到：

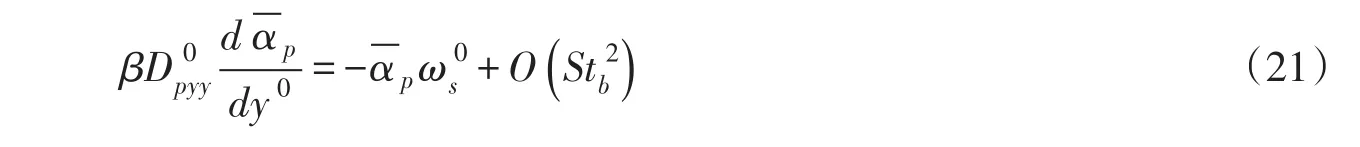
其中 β的表达式为：

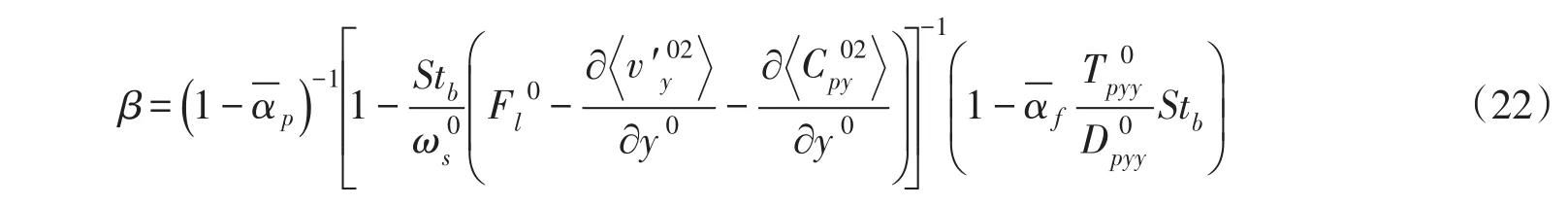
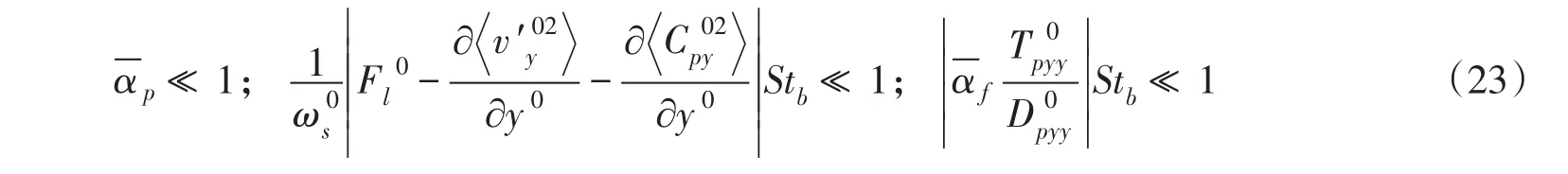
同时满足时， β≈1，即Rouse公式才严格成立。与基于PDF方程得到的扩散方程相比，式（22）增加了正应力的影响。公式中同时出现了修正因子1-，这是由于该理论自然满足浑水连续性的假定，所以在公式中出现了=1-对沉降的影响［2］。另外，从式（22）也可以看出，参数 β受到多种因素的影响，它并不是一个常数，其中颗粒惯性对参数 β的影响较为复杂。为了验证该理论的正确性，Zhong等［18-19］、张磊等［26］开展了系统的研究，与多家实验资料进行了对比验证，结果表明，无论是小颗粒低浓度情形，还是大颗粒高浓度情形，式（18）的计算结果均与实测资料相吻合。在此基础上，Zhang等［27］针对颗粒惯性效应开展了深入研究。结果表明，随着颗粒惯性的增大，颗粒保持其自身运动的能力增强，受到浑水紊动的影响程度降低，颗粒自身紊动以及颗粒碰撞对泥沙扩散的影响显著增强。由此可以看出，颗粒惯性效应对悬移质泥沙扩散的影响十分重要。

3　资料验证

3.1不同扩散模型的对比上述分析给出了不同公式的优缺点和适用条件，同时指出了影响泥沙扩散的多种因素，分析结果如表1所示。结果表明，传统扩散理论仅考虑了重力沉降和水流紊动扩散作用，其只适用于低浓度、小颗粒惯性条件；基于两相流理论的扩散方程，从Cao扩散模型发展到Sne⁃hasis Kundul和Koeli Ghoshal扩散模型，方程中已考虑了颗粒紊动、升力、颗粒惯性、颗粒间相互作用对悬移质运动的影响，适用条件也相应变大，但方程中的重要参数β仍然需要根据试验资料进行率定，这成为了模型应用的限制条件；基于动理学理论下的两种扩散模型，无论泥沙浓度高低、颗粒惯性大小，计算结果均能与实测资料符合较好。但是，由于方程形式较Rouse公式要复杂一些，考虑的影响因素较多，目前在实际工程中应用较少。

3.2资料验证为了进一步说明不同理论下扩散方程的适用性，本文选用了Wang等［28］经典实验中的SF2和SC7组次进行验证。其中SF2为低浓度、小粒径，SC7为高浓度、大粒径。这两组不仅具有代表性，而且不同理论下的扩散方程均已采用该数据进行验证，无需对公式中的经验参数重新率定。实验相关参数见表2，对比结果如图1所示。图中给出的理论计算结果除了传统的Rouse公式及Hunt公式外，同时给出了两相流理论下Cao公式和Snehasis Kundul和Koeli Ghoshal扩散方程以及动理学理论下的弥散方程。为了直观的体现各个公式的准确性，计算了上述各公式的平均相对误差，见表3。从图1和表3可以看出，在低浓度、小颗粒惯性条件下（SF2），五种扩散模型均能够与实测资料相吻合，Cao公式的平均相对误差最大，也仅为8.04%，Snehasis Kundul和Koeli Ghoshal扩散方程的平均相对误差最小，为3.96%；但随着泥沙浓度和颗粒惯性的增大（SC7），Rouse公式、Hunt公式以及Cao公式与实测资料存在着较大偏差，平均相对误差分别为87.86%、73.73%和76.67%，此时已不再适用；Snehasis Kundul和Koeli Ghoshal公式的平均相对误差为10.36%，虽能与实测资料相吻合，但需要根据实测资料率定γ系数的值；而弥散方程则能够在不引进经验参数的条件下，计算值与实测值相吻合，平均相对误差仅为3.77%。

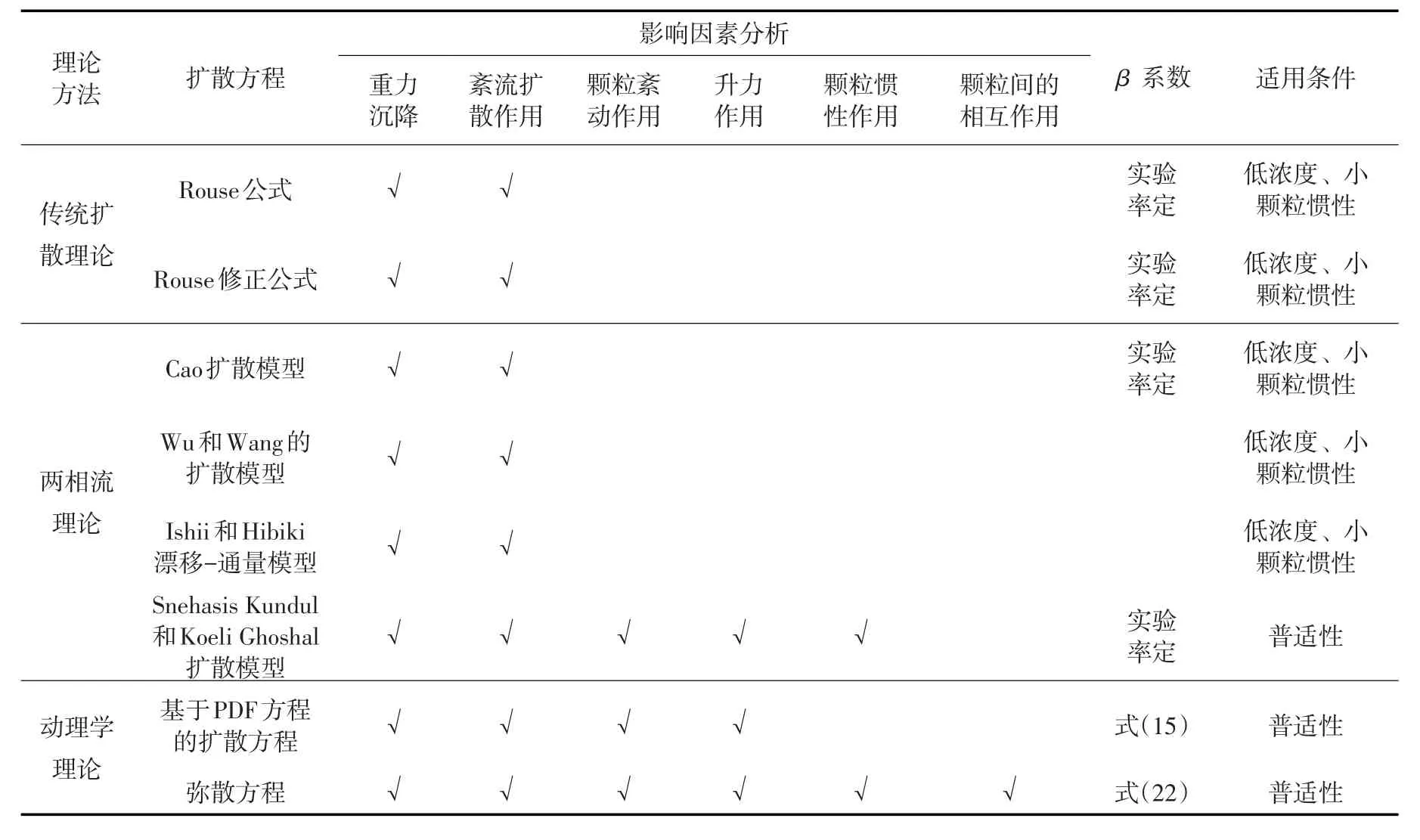
表1　不同理论下扩散方程反映的影响因素和适用条件

表2　Wang和Qian实验组次中的参数值［28］

表3　各公式以及弥散方程的平均相对误差对比结果　（单位：%）

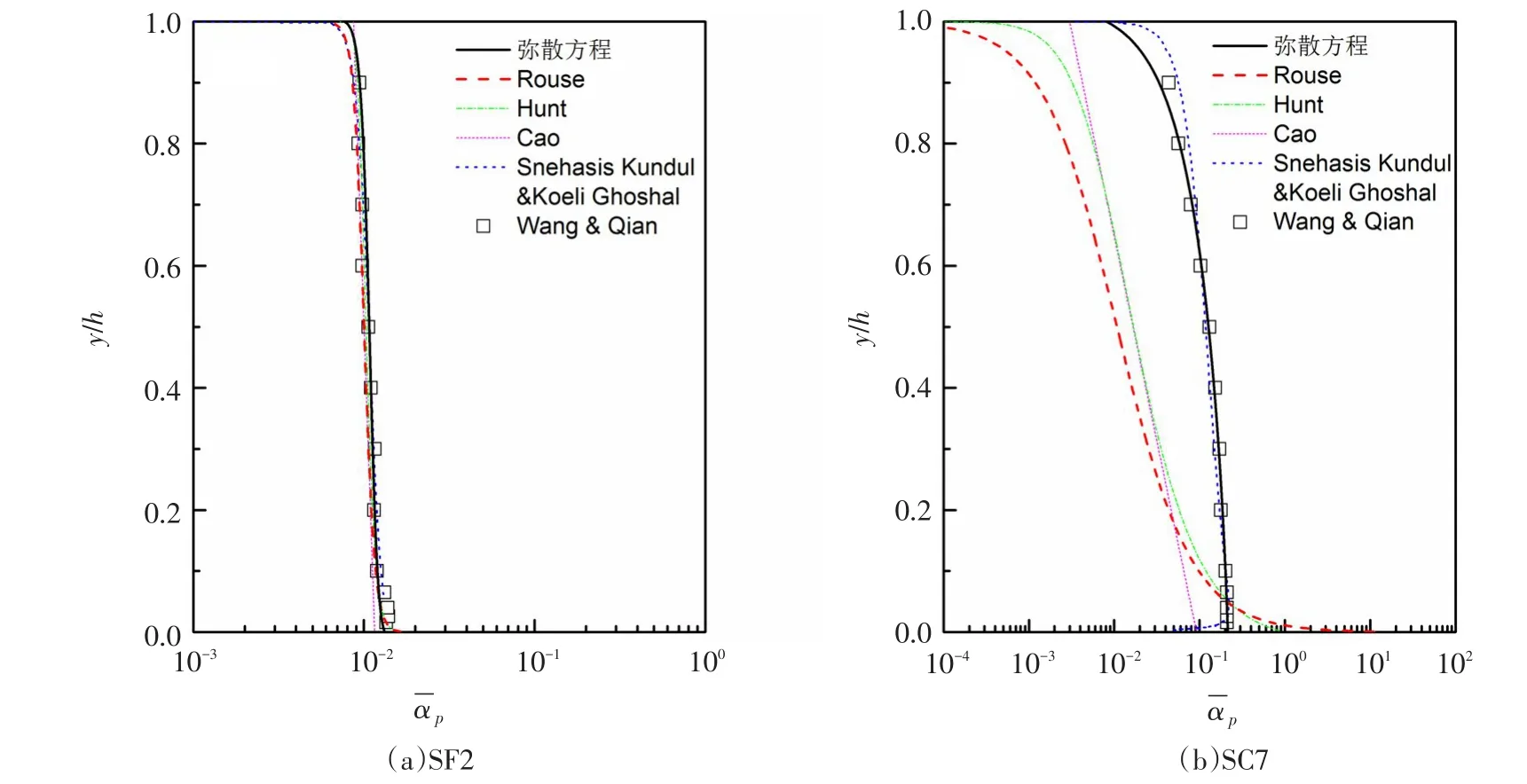
图1　不同扩散方程与Wang&Qian实测资料的对比

4　结论

本文通过对比不同理论下的泥沙扩散方程，分析了各自的适用条件，得到的结论如下：（1）Rouse扩散方程及相关的修正方程均只反映了重力沉降作用及紊流扩散作用对泥沙扩散的影响，参数β更多的依赖于实测资料，公式只适用于低浓度、小颗粒惯性情形。（2）两相流理论下的扩散模型由于忽略了颗粒惯性高阶项的影响，模型也仅适用于颗粒惯性很小的情况；在确定泥沙扩散系数上与Rouse公式面临相同的问题；近期，Snehasis Kundul和Koeli Ghoshal［22］在两相流的基础上，结合Grei⁃mann［23-24］的漂移速度方程以及动理学理论中的应力封闭，提出了新的扩散模型，该模型适用范围较广，反映了颗粒惯性对悬移质浓度分布形式的影响。但是在确定泥沙扩散系数上，采用了类似于 β系数的处理方式，需要根据实测资料进行率定，这在理论上还需进一步完善，实际应用中也会受到限制。（3）在动理学理论下沿着两种不同思路得到的扩散方程，能够反映除了重力沉降及紊流扩散之外的其他作用力对泥沙扩散的影响，其中基于PDF方程的扩散方程体现了颗粒相脉动强度梯度和升力所产生的垂向合力以及颗粒惯性对泥沙扩散的影响；弥散方程则反映出流体惯性、颗粒紊动、颗粒间相互作用以及颗粒惯性等因素（弥散速度本构关系的一阶项）对泥沙扩散的影响。总体来说，两种扩散方程均能够在理论上反映颗粒惯性对悬移质泥沙扩散的影响，公式形式类似，但弥散方程包含的影响因素更多，无论粒径大小、浓度高低，其计算结果均能与实测结果相吻合，全面反映了不同作用机制对泥沙悬浮的影响，有助于我们理解泥沙扩散背后隐藏的力学机理。根据本文所述，对悬移质泥沙的扩散运动已经有了较为深刻的认识，但目前只考虑了均匀沙条件下的悬移质扩散，实际中的河流所携带的泥沙颗粒都是非均匀的，粒径差异较大。未来需考虑泥沙的非均匀性对悬移质泥沙扩散的影响，进一步扩展理论的应用范围，进而形成一个更完整的理论体系。