基于优化时空域频散关系的声波方程有限差分最小二乘逆时偏移

薛 浩 刘 洋 杨宗青

(①中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249； ②中国石油大学(北京)克拉玛依校区石油学院，新疆克拉玛依 834000； ③中国石油大学(北京)CNPC物探重点实验室，北京 102249；④中国石油集团东方地球物理公司西南物探分公司，四川成都 610213)

1 引言

随着油气勘探程度的不断深入，石油勘探的重点已经转向复杂地质构造目标和岩性勘探，并且对勘探精度和计算效率的要求也逐渐提高。偏移方法是对复杂构造成像的一种有效手段，从基于射线的Kirchhoff偏移[1]和Beam偏移[2，3]，发展到基于波动方程的单程波偏移[4-6]和逆时偏移(RTM)[7-9]。由于常规偏移算子是正演算子的共轭转置而不是其逆[10]，受复杂构造及采集条件的影响，常规偏移方法难以满足岩性油气藏勘探开发的需要。为了解决这一问题，国外学者基于Tarantola[11]提出的最小二乘反演理论，提出了最小二乘偏移(LSM)，通过模拟数据与实际数据的匹配求取最佳成像剖面[10]。经过不断的发展，最小二乘偏移从早期的Kirchhoff偏移[12]和单程波波动方程偏移[13]逐渐推广应用到逆时偏移[14-21]中。相比常规逆时偏移方法，基于最小二乘的逆时偏移方法能有效压制偏移噪声，生成分辨率更高、保幅性更好的成像剖面，在成像效果方面更具优势[14-21]。

最小二乘逆时偏移(LSRTM)的关键技术之一是波动方程的求解，因此波动方程的求解精度和效率必然对LSRTM的成像精度和计算效率产生重要影响。波动方程求解方法主要分为三类：有限差分法、伪谱法和有限元法[22]。有限差分法由于计算量较小且实现简单，在地震数值模拟、偏移和反演中已得到广泛应用[22]。在求解波动方程时，通常利用高阶有限差分法计算空间导数[23]。但地震波的传播不仅与空间有关，还与时间有关，采用传统的高阶有限差分法求解差分系数时，一般是基于空间域频散关系，通过对空间导数项进行Taylor级数展开得到，这样会导致较大的频散和误差。为了提高有限差分的模拟精度，Liu等[24，25]基于时空域频散关系，利用平面波理论和Taylor级数展开法提出了一种时空域有限差分法，并将其用于求解声波方程。与传统有限差分法相比，时空域有限差分法的精度和稳定性都得到了提高。为了进一步提高求解精度，许多学者通过采用优化等方式，在求取有限差分系数时，使差分算子最大程度地逼近空间偏导数算子[26-30]。Liu[31]用最小二乘法优化时空域频散关系求解声波方程优化差分系数。与Taylor级数展开方法相比，利用优化时空域频散关系求解差分系数可进一步减小频散，提高模拟精度。

本文在上述研究基础上，将优化的时空域频散关系推广到LSRTM中，在波动方程求解过程中利用优化时空域频散关系求解差分系数。在进行波场外推时，利用混合吸收边界条件处理边界反射。通过Clearbout共轭梯度算法[32]对LSRTM的计算流程进行改进，减少波动方程的求解次数。数值模型的计算结果表明了本文方法的有效性和优越性。

2 基于优化时空域的声波波动方程有限差分法

2.1 基于优化时空域频散关系的声波波动方程差分系数求解

波动方程的求解是最小二乘逆时偏移的关键技术，波动方程求解的精度和效率在一定程度上影响了偏移成像、反演的精度和计算效率。在二维各向同性介质中，声波方程可以写为

(1)

式中：v为速度；p为标量波场；t为时间；x、z为空间坐标。

有限差分算法由于其较高的计算效率和简单的实现方式而被广泛应用于波动方程求解[22]。采用二阶中心差分计算时间二阶导数，可得

(2)

采用高阶差分计算空间导数，可得x和z方向的空间导数为

(3)

(4)

式中cm为差分系数。

将式(2)～式(4)代入式(1)，可得

(5)

≈r-2[-1+cos(ωτ)]

(6)

式中

令kx=kcosθ和kz=ksinθ，其中θ为平面波的传播角度。化简式(6)得到

≈r-2[-1+cos(ωτ)]

(7)

利用泰勒(Taylor)级数展开法展开余弦函数

(8)

比较k2j的系数，可得

(9)

j=1,2,…,M

(10)

当r=0时，相当于只逼近了空间域的频散关系，即只利用了空间导数来求解差分系数。此时求得的是传统有限差分法的差分系数，即由Taylor展开空间域有限差分法求解的。

当r≠0时，相当于逼近了时间域和空间域的频散关系，即利用了空间导数和时间导数同时求解差分系数，此时求得的差分系数为Taylor展开时空域有限差分而得到的。

有限差分的差分系数cm在一定程度上决定了有限差分法的精度和效率，传统的有限差分法是有计算简单、实现方便的特点，但在求解差分系数时只利用泰勒级数展开逼近空间域的频散关系，在中高频区域数值频散迅速增大。为了提高求解波动方程的精度，Liu[31]发展了一种最小二乘优化方法，通过极小化式(7)左端与右端的相对误差这一目标函数逼近时空域的频散关系，从而求得基于优化时空域频散关系的差分系数。优化时空域有限差分法的目标函数为

(11)

令目标函数等于0，可得

(12)

通过求解上述方程组可得优化差分系数cm。

2.2 数值频散分析

相速度的相对误差ξ可用来衡量有限差分法的精度，公式如下[31]

(13)

式中vFD代表数值模拟速度，且有A=cos(mβsinθ)，B=cos(mβcosθ)。

采用一个数值算例对其频散误差进行分析。图1为固定M时，传统有限差分法、Taylor展开时空域有限差分法和优化时空域有限差分法随角度θ变化的频散误差曲线。图2为角度θ固定时，传统有限差分法、Taylor展开时空域有限差分法和优化时空域有限差分法随M变化的频散误差曲线。从图1和图2可看出，随着M的增大，三种方法都能在更大的波数范围内达到较小的误差，Taylor级数展开时空域的有限差分法相比传统有限差分法数值频散要小，优化时空域有限差分法的数值频散更小，精度更高。在误差相差不大时，优化时空域方法的算子长度相比传统的有限差分法的算子长度更短，因此优化时空域方法能够利用较短的算子长度达到传统方法更高的精度，进而提高波动方程的求解效率。

图1 M固定时传统有限差分法(a)、Taylor级数展开时空域有限差分法(b)和优化时空域有限差分法(c)随θ变化的频散误差曲线

图2 θ固定时传统有限差分法(a)、Taylor级数展开时空域有限差分法(b)和优化时空域有限差分法(c)随M变化的频散误差曲线

3 混合吸收边界条件

对不采用吸收边界、采用PML吸收边界[34]和采用混合吸收边界的情况进行数值模拟对比，说明混合吸收边界的吸收效果。为了方便对比，PML吸收边界采用二阶声波方程PML边界条件[34]，边界部分采用指数衰减函数。 均匀介质模型尺寸为

2000m×2000m，速度为3000m/s，空间采样间隔为10m，时间采样间隔为1ms，震源位于模型正中央，震源为一个主频为20Hz的Ricker子波。图4a、图4b和图4c分别为不采用吸收边界、采用10层PML吸收边界和采用10层混合吸收边界情况下三个时刻的波场快照，图4d为在(z=500m，x=1000m)位置处记录的归一化后的波形记录。从图4中可看出，在没有吸收边界的情况下，会有明显的边界反射，采用10层PML吸收边界后，仍然存在一定的边界反射，采用10层混合吸收边界条件后，边界反射几乎完全被吸收。

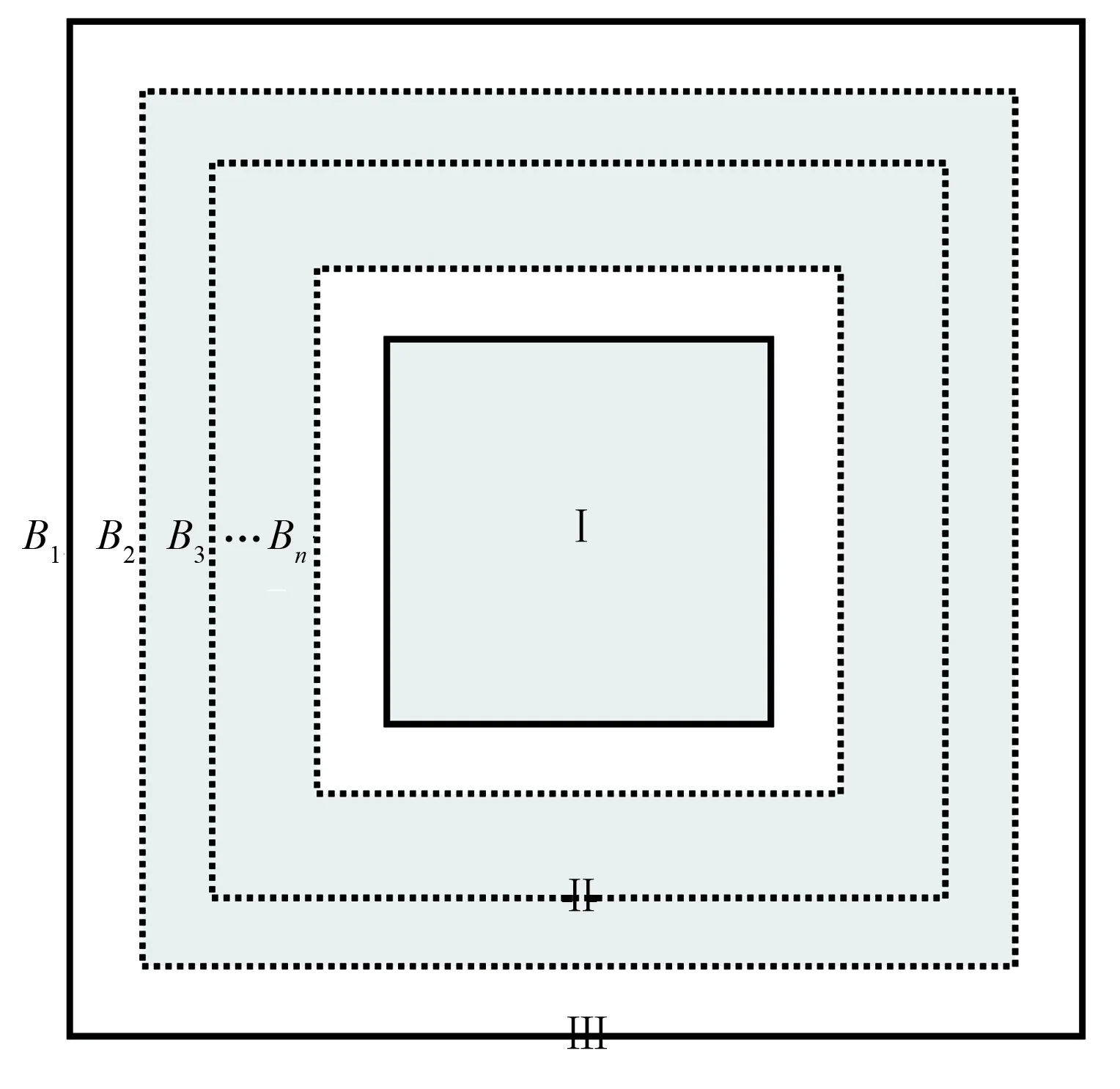
图3 混合吸收边界条件示意图[33]

图4 吸收边界对比图

4 最小二乘法逆时偏移原理及计算流程优化

散射波场的Born正演可写为[16]

(14)

式中：G(g|x)表示震源在x位置、检波点在g位置的格林函数；m为反射系数模型；d为Born正演数据。

方程可写为矩阵形式

d=Lm

(15)

式中L是正演算子。LSRTM成像的目标是用正演数据d估计反射系数

(16)

写成矩阵形式为

m=LTd

(17)

式中偏移算子LT是正演算子L的伴随阵。

为了获得更好的成像结果，成像问题可以当作最小二乘反演问题来处理，目标函数定义为

(18)

迭代最速下降解为

m(k+1)=m(k)-αLT[Lm(k)-d]

(19)

式中：α是步长；k是迭代次数。该式是LSRTM在数据域的迭代。反射系数模型用来生成Born正演数据，通过对观测数据与Born正演数据求差，得到数据的残差； 用残差结果作为输入地震记录进行逆时偏移计算求得梯度，梯度结果用来修正反射系数模型。这个过程一直重复，直至找到一个确定的反射系数模型。

最小二乘逆时偏移通常采用共轭梯度法(CG)求取反射系数模型[18]，计算流程可用图5表示[35]。梯度的计算相当于一次逆时偏移，用边界重建方法实现需要求解正传、重建和反传一共3次波动方程，Born正演需要求解2次波动方程，用线性搜索方法计算步长也需要进行2次Born正演，即求解4次波动方程，每次迭代总共需要求解9次波动方程。Clearbout对共轭梯度方法进行改进，通过求解线性方程组来直接求取搜索步长[32]。

设si为第i次迭代时反射系数模型的更新量，gi为梯度，R为残差，则有

Si=Lsi

(20)

Gi=Lgi

(21)

R=d-Lm

(22)

定义α和β为搜索步长，则αG+βS为共轭梯度法搜索平面，求解目标是找到合适步长，使Q(α,β)=(R-αG-βS)·(R-αG-βS)的值最小。

(23)

求解该方程组可得到系数α和β，然后更新残差和反射系数模型。利用优化CG方法进行LSRTM计算的流程如图6所示。优化CG方法避免了线性搜索中的多次正演，每次迭代减少了4次波动方程的求解，提高了最小二乘逆时偏移的计算效率。

图5 常规LSRTM计算流程[35]图6 优化CG方法的LSRTM计算流程

5 模型试算

正演模拟的精度和效率直接影响反演的精度和效率，利用Taylor级数展开时空域有限差分法和优化时空域有限差分法，分别对均匀模型和Marmousi模型进行数值模拟，分析对比两种有限差分法对正演模拟和LSRTM成像结果的影响。计算过程中，为了提高计算效率，采用了GPU进行加速。

5.1 均匀模型

均匀介质模型的尺寸为4000m×4000m，模型速度为1800m/s，空间采样间隔为20m，时间采样间隔为1ms，震源为50Hz的Ricker子波，震源位于模型正中央。图7a～图7c分别为利用Taylor级数展开时空域有限差分法(M=8、M=30)和优化时空域有限差分法(M=8)得到的2000ms时刻的波场快照； 图7d为从图7a～图7c中x=2000m位置处抽取的单道波形对比。从图7d的波形对比可以看出，当算子长度相同时(M=8)，Taylor级数展开时空域有限差分法(图7a)的数值频散明显高于优化时空域有限差分法(图7c)。算子长度较短时的优化时空域有限差分法(图7c，M=8)与算子长度较长的Taylor级数展开时空域限差分法(图7b，M=30)数值频散相当。在数值频散相差不大的情况下，优化时空域有限差分法可以采用较短的算子长度提高计算效率，在算子长度相同的情况下，优化时空域有限差分法有更高的精度。

图7 均匀介质波场快照对比图

5.2 Marmousi模型

Marmousi速度模型如图8所示，模型尺寸为5000m×3520m，空间采样间隔为10m，震源为50Hz的Ricker子波，震源位于(x=2500m，z=0)。图9a和图9b分别为利用Taylor级数展开时空域有限差分法(M=4)和优化时空域有限差分法(M=4)得到的1800ms时刻的波场快照。图10为得到的单炮地震记录对比图。从图9和图10中可看出，在复杂速度模型情况下，算子长度相同时(M=4)，Taylor级数展开时空域有限差分法(图9a、图10a)的数值频散明显高于优化时空域有限差分法(图9b、图10b)，采用相同的算子长度，对于复杂速度模型，优化时空域有限差分法仍然能获得更高的模拟精度。

用同一模型进行逆时偏移和最小二乘逆时偏移成像，炮点和检波点数目分别为50和353，炮点和检波点均匀分布于地表，炮点间隔为100m，检波点间隔为10m，最小二乘逆时偏移的迭代次数为20次。

图11为反射系数模型，图12为常规逆时偏移经Laplacian滤波后的成像结果。图13a和图13b分别为利用Taylor级数展开时空域有限差分法(M=4)和优化时空域有限差分法(M=4)得到的最小二乘逆时偏移成像结果； 图13c和图13d分别为图13a和图13b的局部放大图。图14为x= 3300m处的反射系数模型(REF)、常规逆时偏移求得的反射系数(RTM)和优化时空域最小二乘逆时偏移求得的反射系数(LSM)对比图。从图11～图14的对比可看出，相比逆时偏移成像，最小二乘逆时偏移成像精度更高、保幅性更好，最小二乘逆时偏移的结果更接近于真实的反射系数模型。

图8 Marmousi速度模型

图9 波场快照对比图

图10 单炮记录对比图

图11 反射系数模型 图12 逆时偏移经Laplacian滤波后成像结果

图13 Marmousi模型的LSRTM成像结果

图15为x= 3300m处的反射系数模型(REF)、Taylor级数展开时空域最小二乘逆时偏移求得的反射系数(TEM)和优化时空域最小二乘逆时偏移求得的反射系数(LSM)对比图。从图11、图13和图15的对比可看出，在差分算子长度相同时，Taylor级数展开时空域有限差分最小二乘逆时偏移和优化时空域有限差分最小二乘逆时偏移在强反射系数界面处都有着较好的成像结果，但在弱反射界面和图13c、图13d红框部分中的高速夹层处，优化时空域有限差分最小二乘逆时偏移具有更高精度的成像结果。图16为Taylor级数展开时空域有限差分最小二乘逆时偏移与优化时空域有限差分最小二乘逆时偏移的收敛曲线对比，可看出优化时空域方法具有更快的收敛速度和更小的残差。

图14 常规逆时偏移与优化时空域最小二乘逆时偏移的单道成像结果(x=3300m处反射系数)对比

图15 Taylor级数展开时空域最小二乘逆时偏移与优化时空域最小二乘逆时偏移的

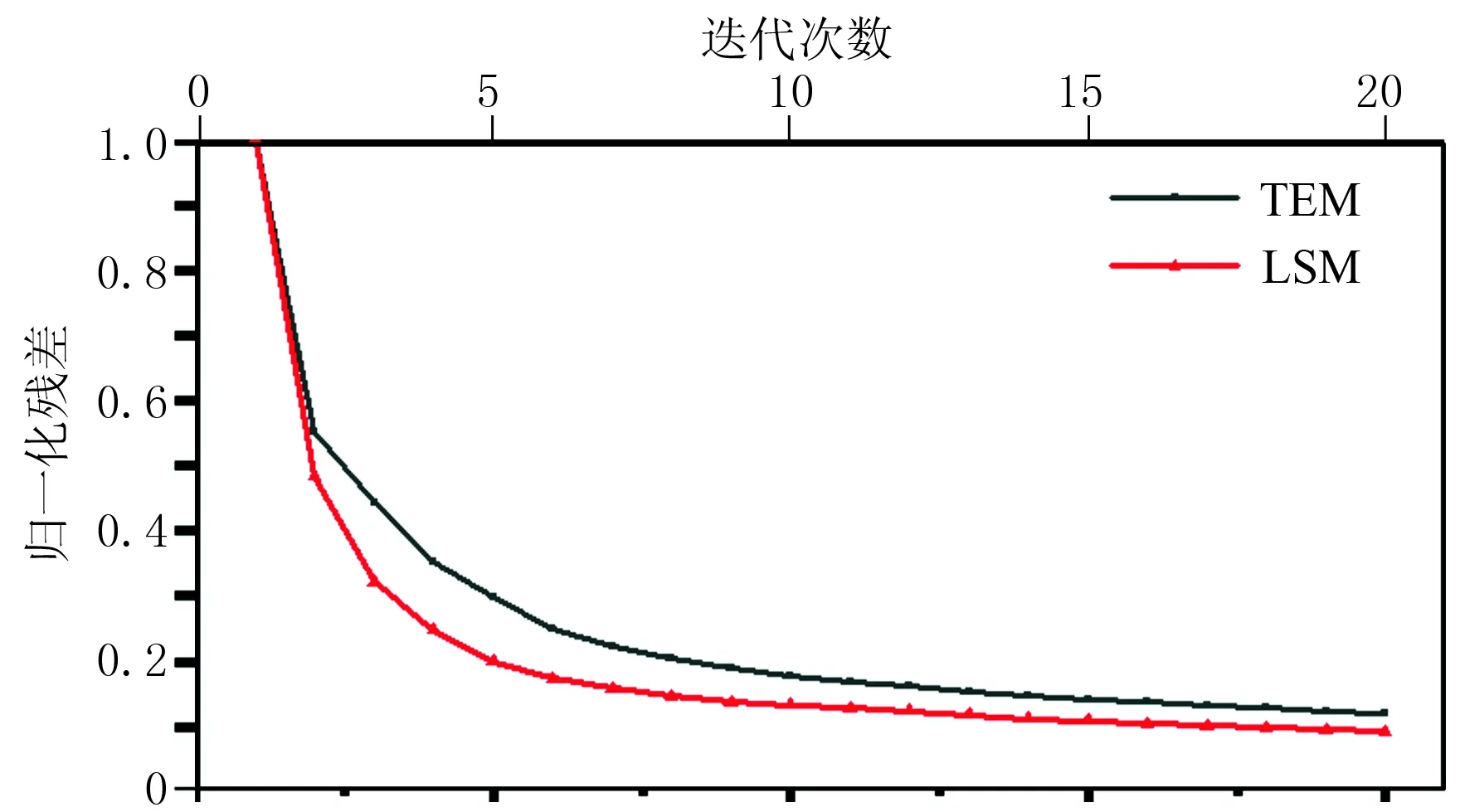
图16 收敛曲线

6 结论

本文将基于优化时空域频散关系的有限差分法推广应用于声波最小二乘逆时偏移中。频散分析和正演模拟表明了优化时空域有限差分法相对于传统的有限差分法和Taylor级数展开时空域有限差分法，能够更有效地压制数值频散，提高数值模拟精度。混合吸收边界条件能较好地压制边界反射。优化的最小二乘逆时偏移计算流程能够减少波动方程的求解次数，提高计算效率。通过对逆时偏移、Taylor时空域最小二乘逆时偏移和优化时空域最小二乘逆时偏移的对比分析，表明最小二乘逆时偏移成像精度高、保幅性好，基于优化时空域频散关系的最小二乘逆时偏移能够对弱反射界面和高速夹层更好成像，能够获得更高精度的成像结果和提高收敛速度。