基于两种时频分析的裂缝性地层阵列声波测井信号时频特征

向 旻 帕尔哈提 张峰玮

(新疆工程学院采矿工程系，新疆乌鲁木齐 830001)

1 引言

声波测井是声学原理在地球物理测井中的重要应用，其核心是运用声波在岩层中的各种传播规律，测量所钻地层的地质和岩石物理参数，从而获取地层的油、气藏的存在与岩性等特征。早期的声波测井只能测量沿着井壁传播的首波(即纵波)到达的时间或幅度。随着技术的进步，阵列声波测井方法在近十几年得到了不断发展。阵列声波测井仪具有多个接收探头，以不同的组合方式接受声波信号。相比于早期的声波测井，其探测深度更大，并且可以接收多种不同类型的波[1-7]。在进行声波测井信号分析时，时间域方法与频率域方法是两类主要的方法[8，9]。但是，由于声波信号是一种非平稳信号，其中任意一种方法都无法避免时间域与频率域的局部化问题[10]，也就是说，如果想要研究信号的时间域信息，就无法同时得到其频率域信息；而如果想要研究信号的频率域信息，就无法同时得到其时间域信息。为了解决这些问题，可以采用时频分析方法对其进行处理。时频分析方法在地学领域已经有了广泛的应用，其种类繁多，主要分为线性与非线性两类。其中，线性方法包括Gabor变换[11]、小波变换[12]、Hilbert-Huang变换[13]、分数阶Fourier变换[14]等；非线性方法又称时频分布，主要包括Cohen类双线性时频分布[15]和Affine类双线性时频分布[16]等。时频分析可以给出信号的时间、频率和幅度三者之间的关系，但是，阵列声波测井信号往往由多种成分组成，且各成分幅度相差很大，这使时频分布图很难将信号所有的成分展现出来，这就应该考虑通过滤波将各组分波分别进行提取。传统的滤波方式主要在频率域进行，而阵列声波测井信号的各组分波之间频率比较接近，所以，频率域滤波往往难以取得良好的效果。

在这些时频分析方法中，结合时频分析的相关数学理论以及笔者近年来的研究[17-19]，本文对时频分析方法进行了改进，利用分数阶Fourier变换的旋转特性对阵列声波测井信号的Born-Jordan分布进行时频域滤波，分别得到纵波和横波的时频分布，改变了传统的频率域滤波对相同频率的不同成分无能为力的缺点，以及过去只能研究整体信号时频特征的劣势。再将纵波和横波的时频分布与原始信号中斯通利波的时频分布相结合，可以探索出一种利用阵列声波测井信号时频特征识别裂缝的新方法。

2 分数阶Fourier变换简介

分数阶Fourier变换是一种新兴的且发展很快的时频分析方法，由Condon于1937年提出。在随后的数十年中，Namias[20]、McBride等[21]、 Loh-mann[22]、Almeida[23]以及Shih[24]陆续发展了其数学理论。1995年Shih提出了一种分数阶Fourier变换的定义形式——态函数叠加的方法。他利用经典Fourier变换整数幂运算的4周期性质将分数阶Fourier变换定义成4个态函数的线性组合，其组合系数是分数阶Fourier变换幂次的函数。

(1)连续性公理，即分数阶Fourier变换是连续性的变换；

(2)边界性公理，即当α是整数时，分数阶Fourier变换等价于经典Fourier变换；

(3)交换可加性公理，即对于任意的α和β，分数阶Fourier变换的阶数具有可加性，即

(1)

则该信号α阶分数阶Fourier变换可写成

(2)

式中：g0(t)=g(t)，g1(t)=F[g0(t)]，g2(t)=F[g1(t)]，g3(t)=F[g2(t)]；t为时间；j表示第j个分量。

分数阶Fourier变换具有一种独特的旋转特性，利用这一性质，可以获得某一信号在不同阶数下的时频分布。

3 Born-Jordan分布简介

1966年，Cohen提出了具有双线性形式时频分布的一般表达式[25]。对于信号g(t)，其Cohen类时频分布表达式可以写为

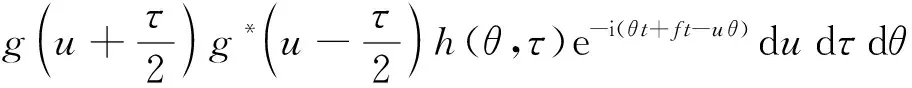
(3)

式中:f为频率；h(θ,τ)为核函数;θ为核函数中的频率变量；μ为过渡时间变量；τ为核函数中的时间变量。

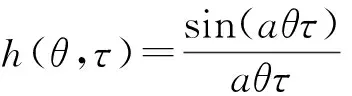
(4)

式中a是常数。

BJDg(t,f)

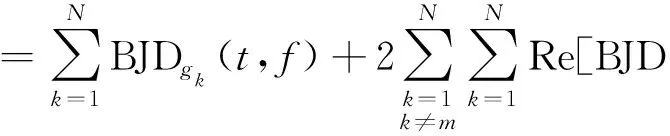
(5)

4 不同性质地层的阵列声波测井信号时频特征

本文涉及的所有数据均来自中国大陆科学钻探(CCSD)，仪器采用阿特拉斯公司制造的多极子阵列声波测井仪(MAC)。 图1包括了某地层阵列声波测井原始信号及其Born-Jordan分布。由于幅度与能量呈正相关的关系，所以信号的幅度特征可以用来衡量能量的分布情况。利用阵列声波测井原始信号只能得到信号的时间域信息，不能同时得到信号的频率域信息，而利用该信号的Born-Jordan分布，可以同时得到信号的时间域和频率域信息，但是信号中的斯通利波幅度远高于其他各组分波，以至于其他各组分波难以在图中显示，无法有效识别。

图1 阵列声波测井原始信号(a)及其Born-Jordan分布(b)

分数阶Fourier变换具有一种独特的时频域旋转特性，而不同的旋转角度则代表不同的域。对于分数阶Fourier变换，当阶数α=0时，相当于信号没有进行变换，反映信号的时间域信息；当阶数α=1时，相当于对信号进行了传统Fourier变换，反映信号的频率域信息；而当阶数在0～1之间时，则反映信号在时间域和频率域之间的某一过渡域的信息。将不同阶数的分数阶Fourier变换与Born-Jordan分布相结合，可以得到处于不同域的信号的时频分布。不同域的信号在时频分布图中具有不同的时间和频率特征，因此，利用这一特点可以在时频域进行滤波，以获取各组分波的时频特征。

本文所介绍的方法具体步骤如下。

首先，提取横波的时频分布。对图1中的阵列声波测井信号做高通滤波，截止频率f1=5kHz，滤去幅度较高的低频斯通利波，结果如图2所示(为了直观，处理的过程采用二维影像图)。

可以看出，传统的频率域滤波并不能滤除频率与横波接近的斯通利波及伪瑞利波。这时，对图2做0.5阶分数阶Fourier变换，结果如图3所示。

由于信号所处的域发生了变化，所以信号的时间与频率也发生了变化。这样可以选取截止频率f2=13kHz，对信号进行高通滤波。之后，再做-0.5阶分数阶Fourier变换，对信号所处的域进行还原，结果如图4所示。

图4中横波已基本提取完毕，但之前的两次滤波主要针对频率与横波相近或者低于横波的斯通利波和伪瑞利波，频率略高于横波的成分也会有所残留，所以可以对图4数据做-0.3阶分数阶Fourier变换，结果如图5所示。

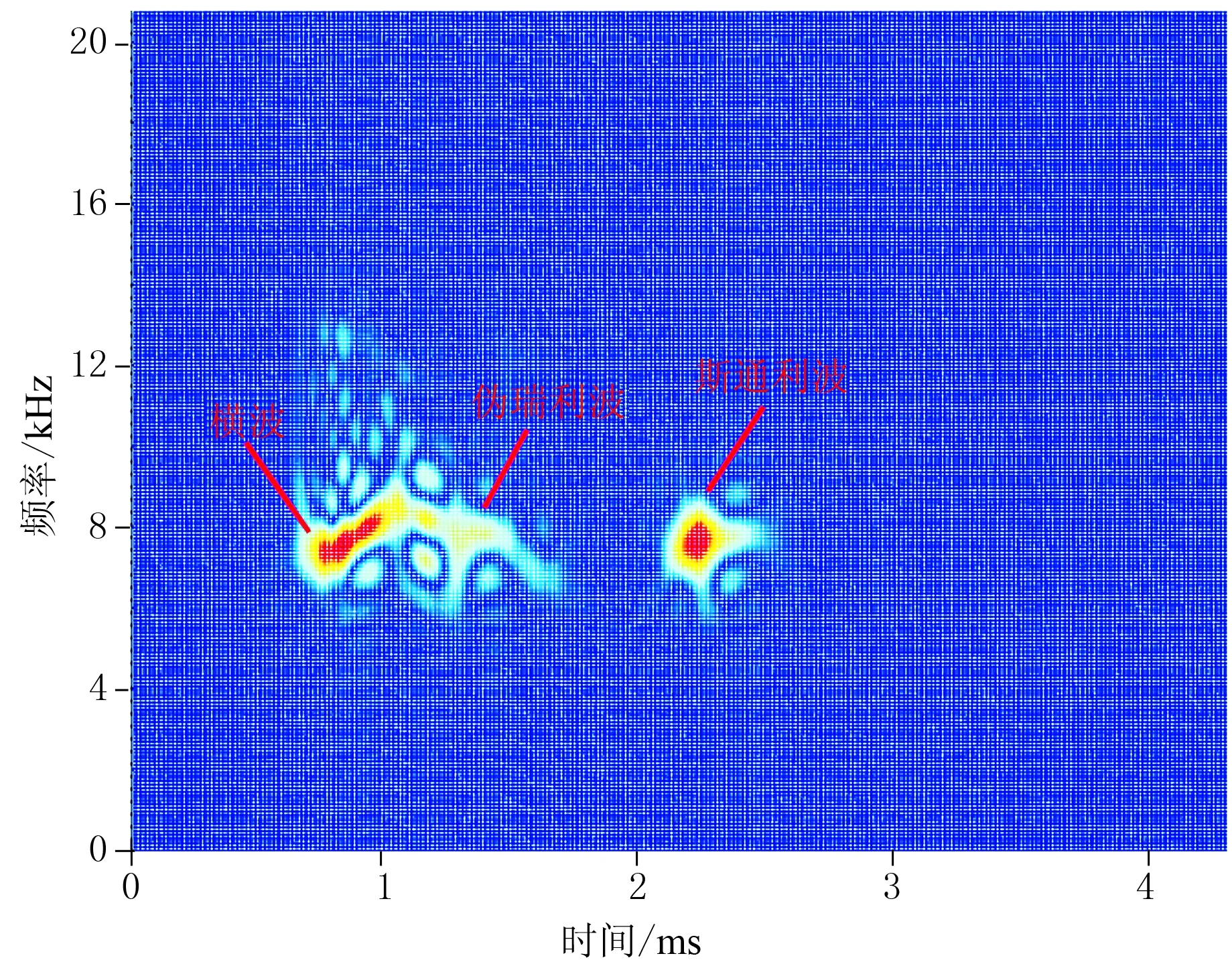
图2 滤除低频斯通利波后信号的Born-Jordan分布

图3 对图2做0.5阶分数阶Fourier变换后的

选取截止频率f3=4kHz，对信号进行低通滤波。之后，再做0.3阶分数阶Fourier变换，将信号所处的域进行还原。这样就得到了横波的时频分布(图6)。

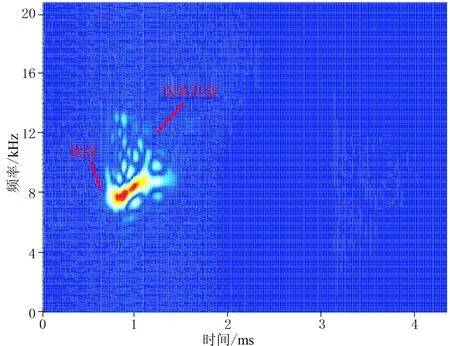
图4 第二次高通滤波后信号的Born-Jordan分布

图5 对图4数据做-0.3阶分数阶Fourier变换后的

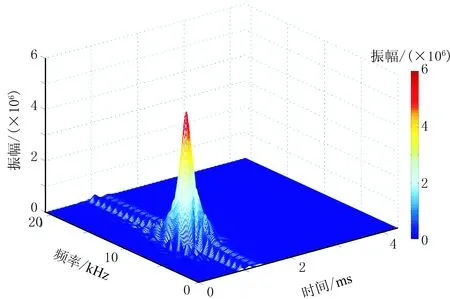
图6 横波的Born-Jordan分布

然后，提取纵波的时频分布。提取纵波的步骤与提取横波基本一致，只需把上述3个截止频率分别设为f1=10kHz、f2=16kHz以及f3=3kHz即可。图7为纵波的时频分布。

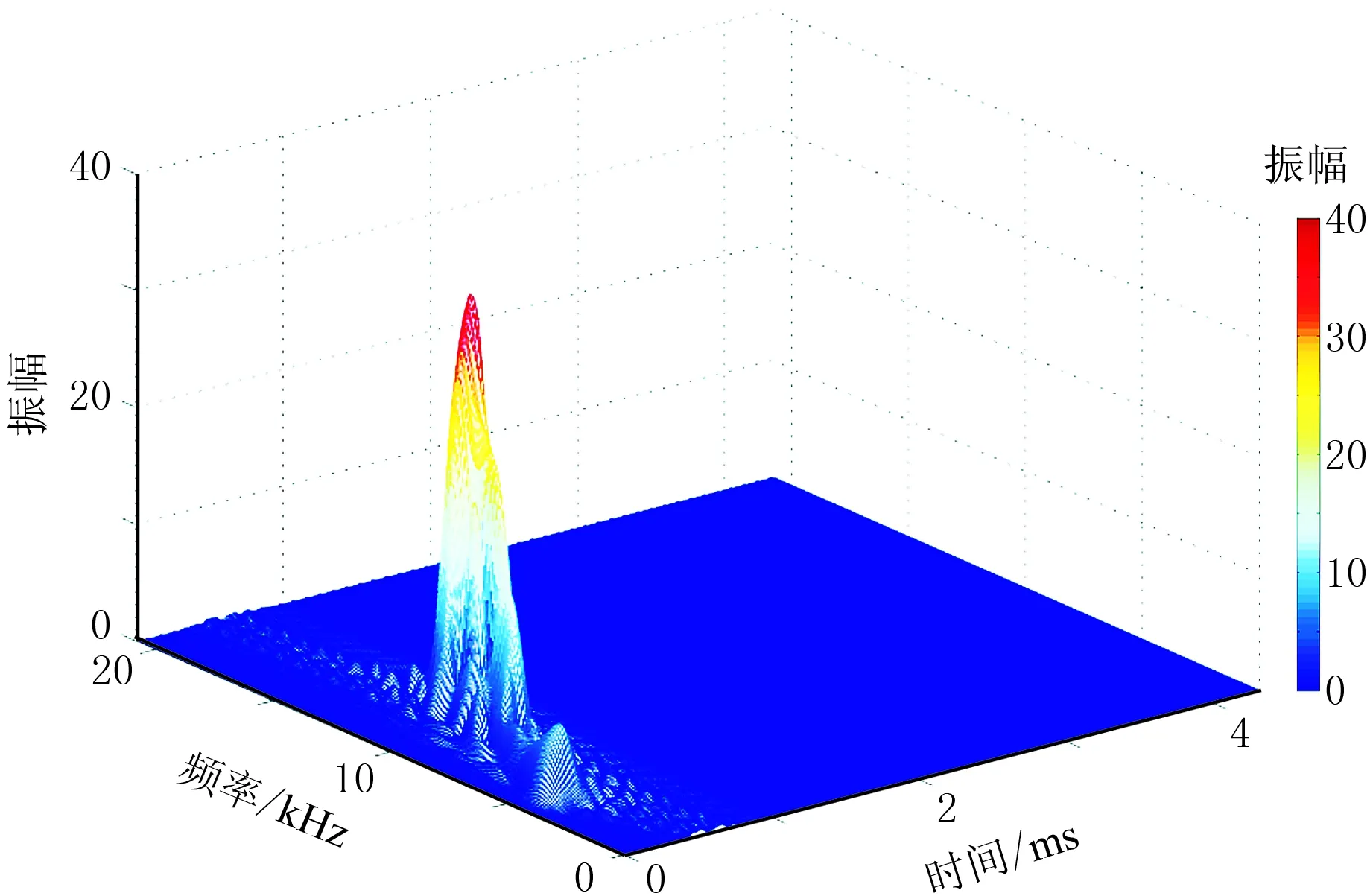
图7 纵波的Born-Jordan分布

下面分别选取致密性地层和裂缝性地层通过上述手段进行研究。

图8为CCSD井660m处典型致密性地层的测井信号及Born-Jordan分布。纵波位于0.3～0.6ms、10～13kHz之间，主频约为11.5kHz，波峰的幅度大约为20左右；横波位于0.8～1.1ms、 6～10kHz之间，主频约为8kHz，波峰的幅度大约为2.5×104；斯通利波位于2～3ms、 0～10kHz之间，以低频为主，主频约为3kHz，波峰的幅度大约为4×106；伪瑞利波的时间跨度比较大，波至时间略晚于横波，一直持续到波列最后，幅度相对较低，波峰幅度约为5×103。整体来看，由于该处是典型的致密地层，未见明显的构造现象，各组分波的时间、频率和幅度不会出现异常变化，所以，可将图8作为本文的参照标准。

图9为CCSD井606m处的构造破碎带的测井信号及Born-Jordan分布。纵波位于0.5～0.8ms、9～12kHz之间，主频约为10.5kHz，波峰的幅度大约为0.18；横波位于0.8～1.2ms、4～10kHz之间，主频约为7kHz，波峰的幅度大约为4×103；斯通利波位于2.1～2.9ms、0～10kHz之间，以低频为主，主频约为3kHz，波峰的幅度大约为1.0×104；伪瑞利波有1个比较明显的波峰，位于3.5ms、3kHz，幅度约为5.0×103。

图10为CCSD井704m处的构造破碎带的测井信号及Born-Jordan分布。纵波位于0.5～0.8ms、9～12kHz之间，主频约为10.5kHz，波峰的幅度大约为1.5；横波位于0.8～1.2ms、5.0～10kHz之间，主频约为7kHz，波峰的幅度大约为60；斯通利波位于2.1～2.9ms、0～10kHz之间，以低频为主，主频约为3kHz，波峰的幅度大约为4.0×103；伪瑞利波出现了2个波峰，分别位于0.5～0.8ms、9～12kHz之 间，主频约为10.5kHz，波峰的幅度大约为10；横波位于0.8～1.2ms、5～10kHz之间，主频约为7kHz，波峰的幅度大约为700； 斯通利波位于2.5～3.0ms、0～10kHz之间，以低频为主，主频约为3kHz，波峰的幅度大约为4×103； 伪瑞利波有一个比较明显的波峰，位于3ms、3kHz，幅度为4.2×103左右。

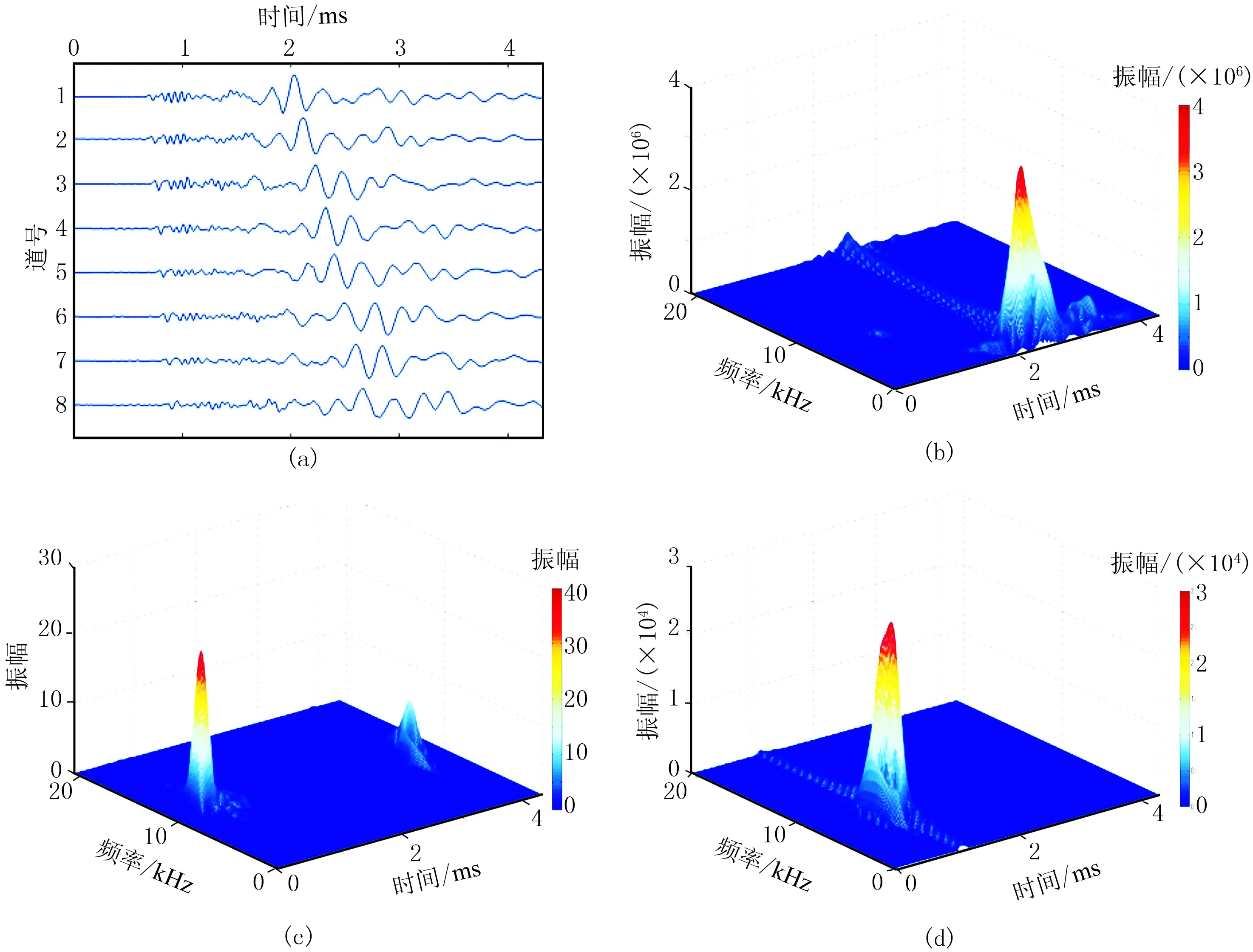
图8 660m处阵列声波测井信号及其Born-Jordan分布

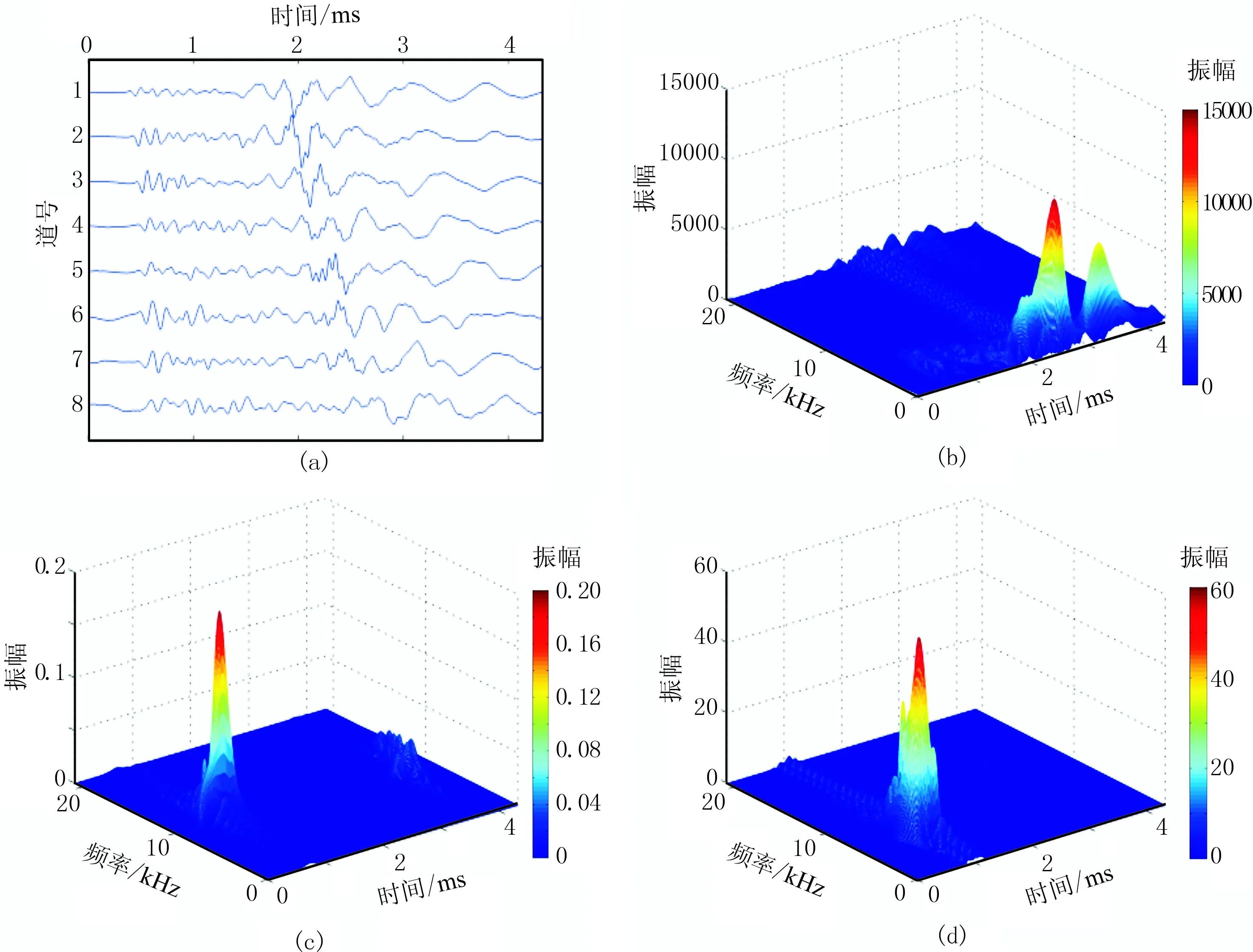
图9 606m处阵列声波测井信号及其Born-Jordan分布

图10 704m处阵列声波测井信号及其Born-Jordan分布

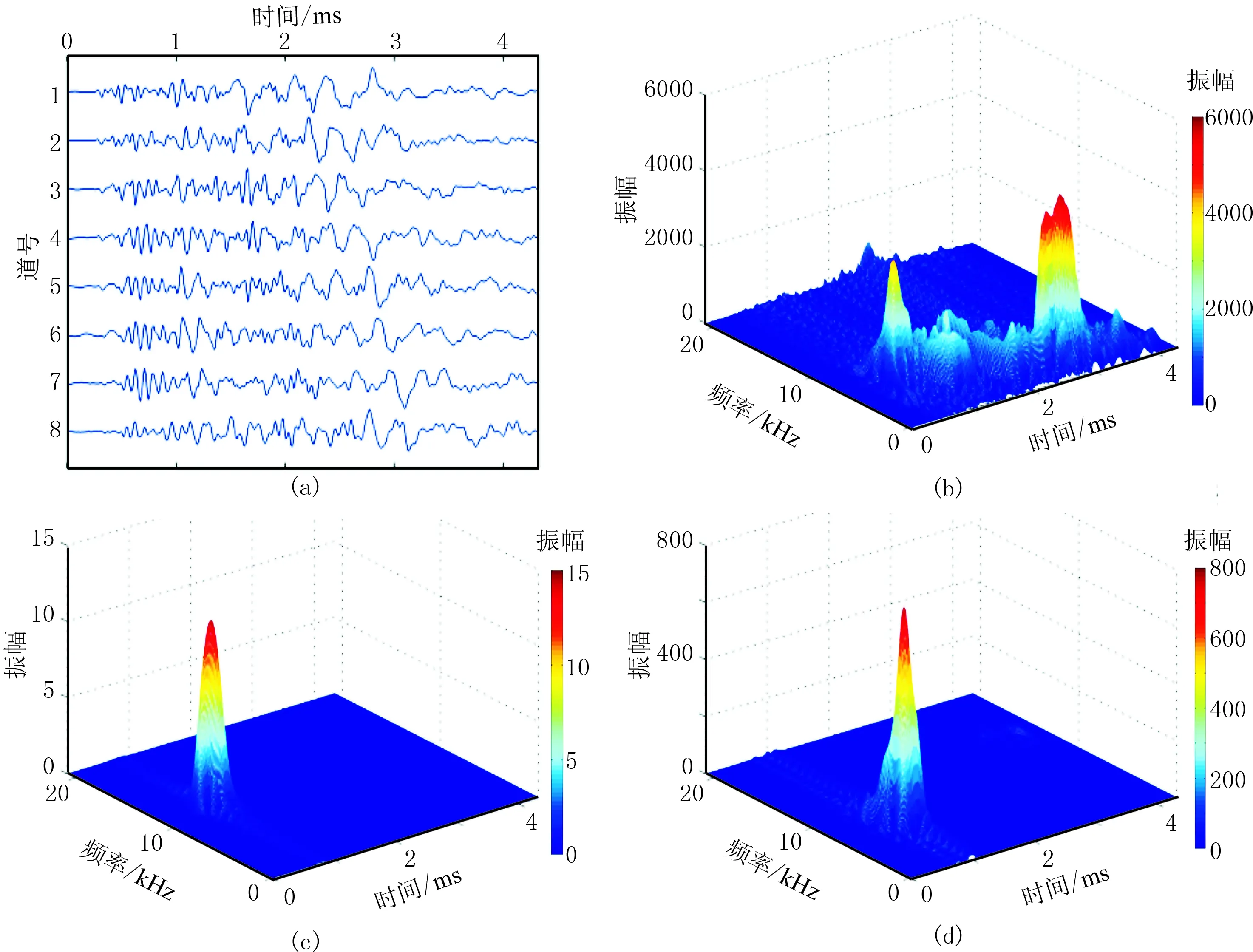
图11 842m处阵列声波测井信号及其Born-Jordan分布

将图9、图10、图11与图8进行对比，可以总结出裂缝性地层的时频特征。

第一，从声波全波列时频分布图来看，对于致密性地层，由于斯通利波的幅度远高于纵波、横波和伪瑞利波，所以只会出现一个明显的波峰，由低频斯通利波产生；而对于裂缝性地层，波峰的数量至少为2个，除了斯通利波以外，可能由横波或者伪瑞利波产生。斯通利波是一种低频、低速、且能量较高的面波。斯通利波对于渗透性地层十分敏感，其能量会随着井中流体流入地层而大量衰减。因此，相比于致密性地层，裂缝性地层中的斯通利波幅度要低2个数量级以上，且所处时间段缩短。由于裂缝性地层中的斯通利波衰减程度远大于纵波、横波和伪瑞利波，所以，斯通利波与纵波、横波和伪瑞利波之间的幅度差距明显缩小，这使得横波和伪瑞利波均能够明显地出现在声波全波列时频分布图中。

第二，相比于致密性地层，裂缝性地层中纵波的波至时间较晚，主频较低，而幅度也较低。这其中时间的变化与地层的弹性特征有关。根据纵波速度公式

(6)

纵波能量的衰减主要与质点振动时摩擦产生热损耗有关，密度越低，热损耗越大。由于裂缝性地层的密度小于致密性地层，所以相比于致密性地层，裂缝性地层中的纵波幅度会出现更严重的衰减，而衰减程度则由裂缝的角度、密度、尺寸等多方面因素综合决定，因此并无明显规律可循。

相比于致密性地层，裂缝性地层中纵波的主频也会降低，这是由于高频部分质点的振动更快，所以摩擦产生的热损耗也就越多，造成了高频部分的能量相比低频部分衰减更剧烈，因此裂缝性地层纵波主频出现了降低的现象。

第三，横波的变化主要体现在幅度上，而在速度和主频上变化不大。横波能量的衰减也与地层密度成负相关的关系。相比于致密性地层，裂缝性地层中的横波幅度会出现更严重的衰减。

根据横波速度公式

(7)

由式(7)可见，横波速度与剪切模量成正相关的关系，而与密度成负相关的关系。相对于致密性地层，在裂缝性地层中，剪切模量和密度在数值上的减小程度相当，使得二者的比值无明显改变，所以造成横波速度及横波的波至时间无明显变化。

除波至时间以外，在致密性地层和裂缝性地层中横波的主频也没有太大的变化。这主要是由于横波的能量较高，高频部分较快的质点振动所带来的能量损耗，并不会显著降低横波各频率成分能量的相对大小，因而使得横波的主频未明显降低。

第四，伪瑞利波时间和频率跨度较大，二者在致密性地层和裂缝性地层中几乎没有区别。而伪瑞利波的幅度变化规律性比较差，相比于致密性地层，裂缝性地层中斯通利波之前的伪瑞利波幅度会出现一些不规则的降低，而斯通利波之后的伪瑞利波的幅度则无明显变化。

5 结论与讨论

利用分数阶Fourier变换对阵列声波测井信号的Born-Jordan分布进行时频域滤波，能够获取信号各组分波的时频特征，便于研究声波信号在不同性质地层中的时频分布规律。根据文中的一系列探索，可以得到如下结论。

(1)在声波全波列时频分布图中，对于致密性地层而言，斯通利波幅度远高于纵波、横波和伪瑞利波，因而往往只有斯通利波一个明显的波峰；而对于裂缝性地层而言，斯通利波能量出现显著衰减，所以往往会出现2个以上的波峰，由斯通利波及横波或者伪瑞利波形成。

(2)在纵波时频分布图中，相对于致密性地层而言，裂缝性地层中的纵波由于体积模量、剪切模量的减小，热损耗增加，其波至时间延迟，主频降低，同时幅度衰减增大。

(3)在横波时频分布图中，相对于致密性地层而言，裂缝性地层中的横波由于热损耗的增加，其幅度衰减增大。而该井中的几处裂缝未明显改变剪切模量与密度的比值，所以横波波至时间没有差异。同时，横波本身能量较高，裂缝性地层也未改变横波各频率成分能量相对大小，因而各地层横波主频也未发生明显变化。

(4)相对于致密性地层而言，裂缝性地层中的伪瑞利波在时间和频率特征上未出现明显变化，而在幅度上，斯通利波之前的伪瑞利波幅度会出现一些不规则的降低，而斯通利波之后的伪瑞利波的幅度则无明显变化。

本文所介绍的方法很大程度上利用了分数阶Fourier变换的旋转特性，通过改变阶数得到需要的图像，继而进行时频域滤波。阶数的选择并不是一成不变的，其与声源的激发频率有关，可以根据实际情况灵活选取。而Born-Jordan分布则是一种Cohen类双线性时频分布。除此以外，Cohen类时频分布的成员很多，如Wigner分布、Page分布、Rihaczek分布等，不同的分布具有不同的优点。为了获得不同的效果，上述Cohen类时频分布大都可以与分数阶Fourier变换相结合。笔者将在这些方面开展进一步的研究。