含裂缝致密砂岩多波AVO响应分析

杨 帅 芦 俊* 杨 春

(①中国地质大学(北京)能源学院，北京 100083； ②中国地质大学(北京)地球物理与信息技术学院，北京 100083)

1 引言

致密砂岩储层中的裂缝是良好的油气储集空间和运移通道[1]，因此研究致密砂岩中裂缝的发育程度对致密砂岩储层的预测与评估具有重要意义[2-4]。致密砂岩中存在的水平缝，一般会受上覆地层压力作用而张开度变小，甚至完全闭合，对油气产能的改善作用有限，而高角度和近似于垂直的裂缝有利于改善储层的渗透性，是油气勘探关注的重点[5，6]。含高角度或近似垂直裂缝的致密砂岩在地震学上被描述为HTI介质，即具有水平对称轴的横向各向同性介质[7]，其地震波反射系数与裂缝密度和充填流体性质有关。对含裂缝介质进行正演模拟，研究其地震响应特征，对于了解裂缝性质并对裂缝发育进行预测具有重要意义[8，9]。为了研究地下裂缝介质与地震波响应之间的关系，地球物理学者进行了大量研究。Hudson[10-14]推导了岩石弹性模量对裂缝密度的一阶和二阶扰动量，给出了含定向裂缝介质的弹性模量的计算方法，但由于其理论假设裂隙间没有流体流动，所以只适用于高频情况；Schoenberg等[15-18]在位移不连续和旋转不变性的假设下，不考虑裂缝的形状与结构，提出了线性滑移理论；Thomsen[19-22]提出了裂缝介质的弱各向异性理论，给出了用各向异性参数表征的相速度公式，认为裂缝型岩石即为在各向同性介质中包含了一套与等径孔隙液压相连通的裂隙，流体可以在裂缝和孔隙之间流动。该理论相比于Hudson理论和Schoenberg理论更适用于地震尺度下饱含流体HTI介质的地震波响应特征分析。

近年来，随着地震采集与处理技术的发展，运用地震手段预测地下裂缝成为了研究热点，其中AVO和AVA方法是地震勘探检测裂缝的重要技术。Rüger等[23-28]推导了弱各向异性介质中反射系数近似公式，并运用纵波方位AVO检测裂缝； Pérez等[29]将纵波AVO技术用于实际数据的裂缝检测； Mallick等[30]研究了海洋三维地震资料反射系数与裂缝方位之间的关系；Gray等[31]基于纵波方位AVA特征，预测了Manderson油田的裂缝； Hall等[32]用海底三分量地震数据进行了纵波AVO分析及天然裂缝的识别；乐邵东[33]运用AVA技术预测川西地区JM构造裂缝； 郝守玲等[34]、齐宇等[35]、杨勤勇等[36]通过物理实验模拟了裂缝介质的纵波方位各向异性；李国发等[37]利用三维纵波AVO技术检测了煤层中发育的裂缝； 王宏伟等[38]基于HTI介质理论对构造煤的方位AVO响应进行了正演分析； 李慧琼等[39]对鄂尔多斯盆地黄257井区基于纵波方位AVA对裂缝分布进行了预测；印兴耀等[40，41]提出稳定方位AVO梯度和各向异性梯度反演方法预测裂缝性储层； 薛娇等[42]基于等效裂缝介质模型对裂缝参数进行AVOA反演。

本文以四川新场地区须家河组致密砂岩为例，基于Thomsen各向异性理论，在均匀背景介质中，运用Biot-Gassmann方程[43，44]计算背景介质饱和流体的弹性模量，再通过Thomsen各向异性理论计算含裂缝储层的宏观各向异性参数及弹性参数。最后，通过Rüger的HTI介质地震波反射系数近似公式进行AVO正演模拟与分析。

2 含裂缝致密砂岩模型

2.1 饱和流体岩石的弹性模量

运用Biot-Gassmann方程[44]计算饱含流体各向同性岩石体积模量和密度

式中：φ为总孔隙度；ρm、ρf、ρsat分别为岩石骨架、流体、饱和流体岩石的密度；Kd、Km、Kf、Ksat分别为干岩石、岩石骨架、流体、饱和流体岩石的体积模量。其中Kf和密度ρf由Wood方程计算

其中：Kw、Ko、Kg分别是水、油和气体的体积模量；Sw、So、Sg分别是水、油和气体的饱和度。根据饱和流体岩石的体积模量、密度可计算纵、横波速度

(5)

(6)

其中饱和流体岩石的剪切模量μsat因为不受流体影响，等于干岩石的剪切模量。根据四川新场须家河组致密砂岩测井数据[45]计算致密砂岩岩石模量(表1)，进一步可以计算出饱和流体致密砂岩的纵、横波速度与密度，以及裂缝碎屑充填物的纵、横波速度与密度(表2)。

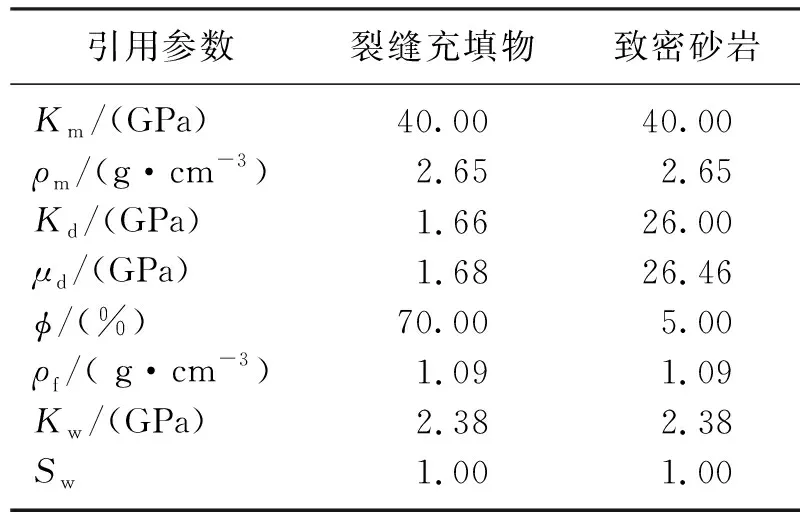
表1 致密砂岩岩石物理参数

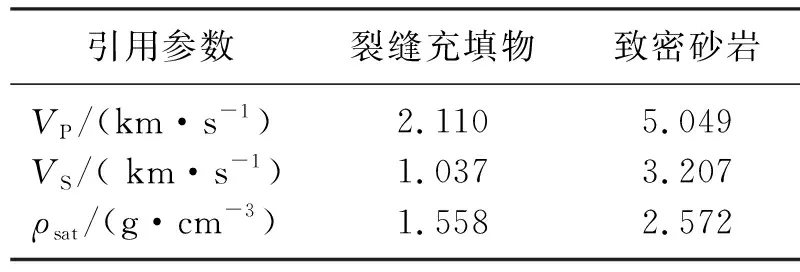
表2 裂缝充填物与致密砂岩纵、横波速度及密度计算结果

2.2 HTI介质的等效各向异性与弹性参数

当入射纵波在HTI介质中反射时，若裂缝面与入射面斜交，会产生三种反射波：反射纵波(PP波)，反射快横波(PS1波)，反射慢横波(PS2波)。如图1所示，快横波的偏振方向平行于裂缝面，而慢横波的偏振方向垂直于裂缝面。

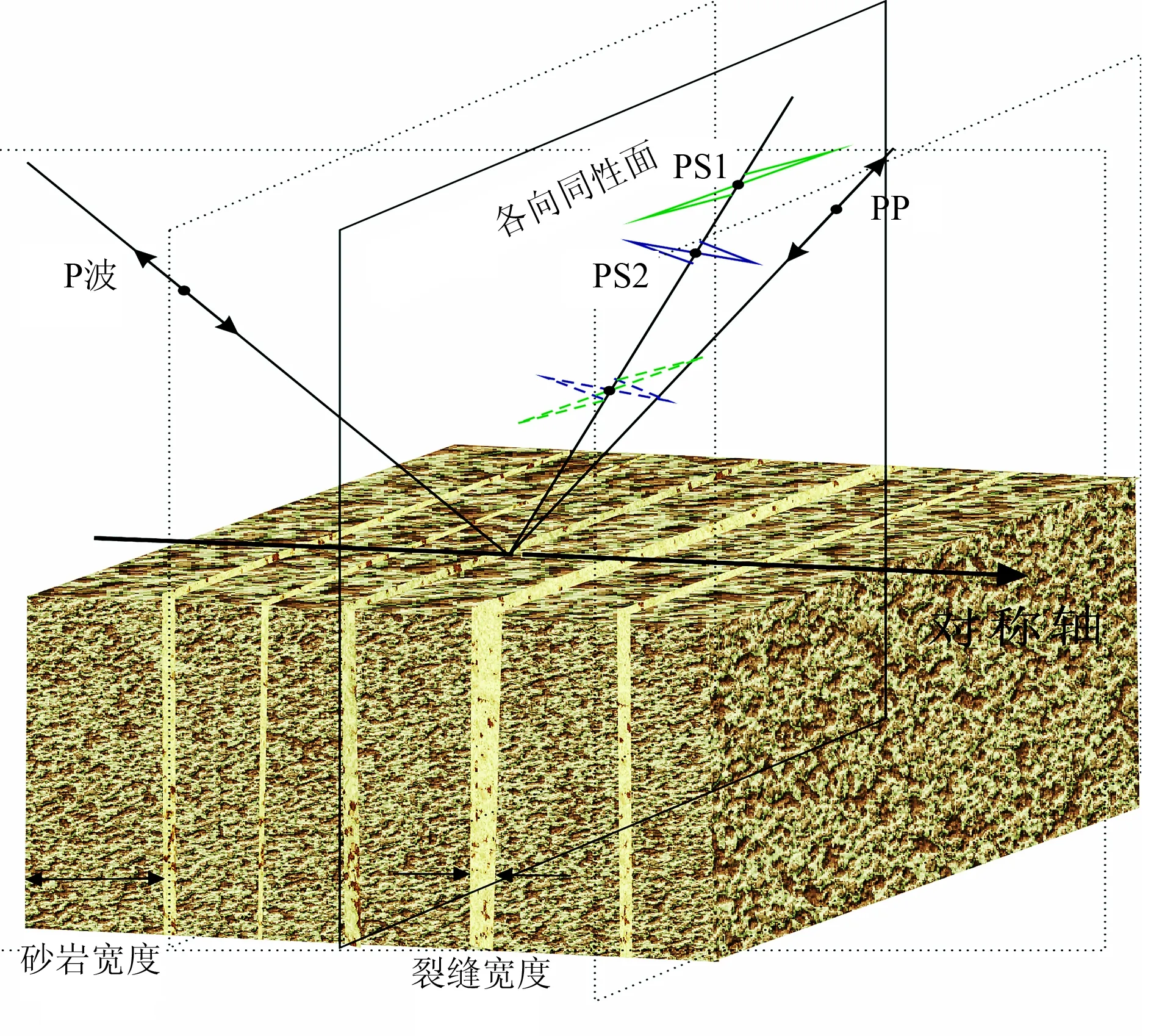
图1 HTI介质反射波示意图

在HTI介质中，刚度系数矩阵[22]可表示为

(7)

根据Thomsen各向异性介质理论，HTI介质的等效各向异性参数和弹性参数可由上式中的刚度系数cij计算[22]

(8)

式中：α表示纵波的垂向速度；β表示快横波的垂向速度；ε(V)为纵波水平速度和垂直速度的差值与纵波垂直速度的比值，表示纵波的各向异性程度；δ(V)

表示纵波和横波各向异性相对大小；γ指垂直传播的横波速度和水平传播的横波速度差值与横波水平速度的比值，表示横波速度的各向异性程度；上标“V”表示垂直方向。

HTI介质的刚度系数cij可由裂缝和背景砂岩的弹性参数计算[46]

(9)

式中〈·〉表示以裂缝和背景砂岩的宽度(图1)为权系数的加权平均值。通过裂缝宽度a、裂缝充填物的孔隙度φc、裂缝长度c可以计算裂缝密度e=3aφc/(4πc)。根据式(8)、式(9)以及表2参数可以计算出不同裂缝密度下饱和流体裂缝致密砂岩的等效各向异性参数及弹性参数(表3)。

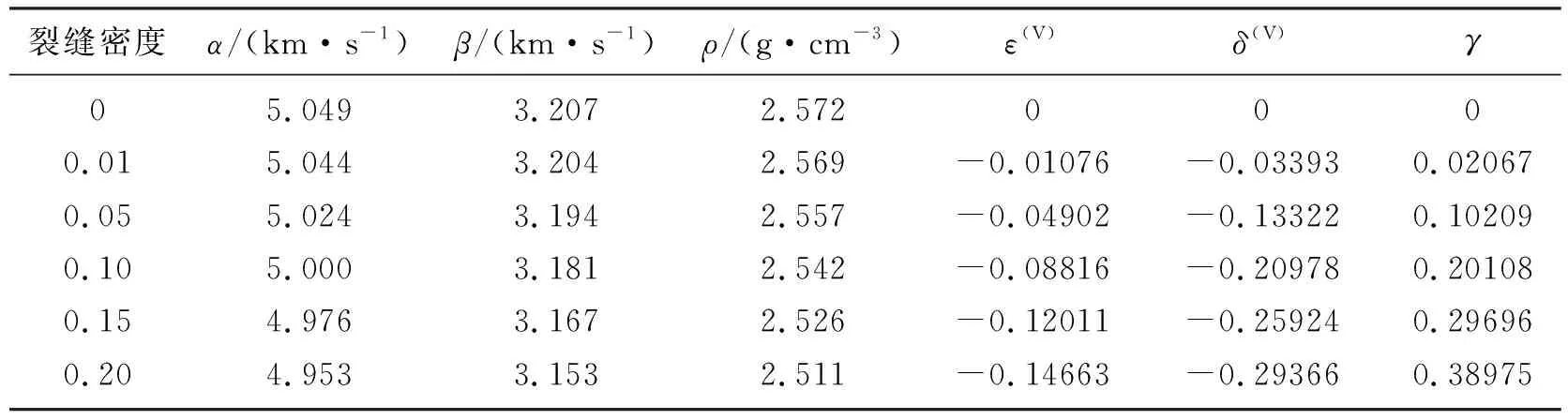
表3 不同裂缝密度致密砂岩模型参数

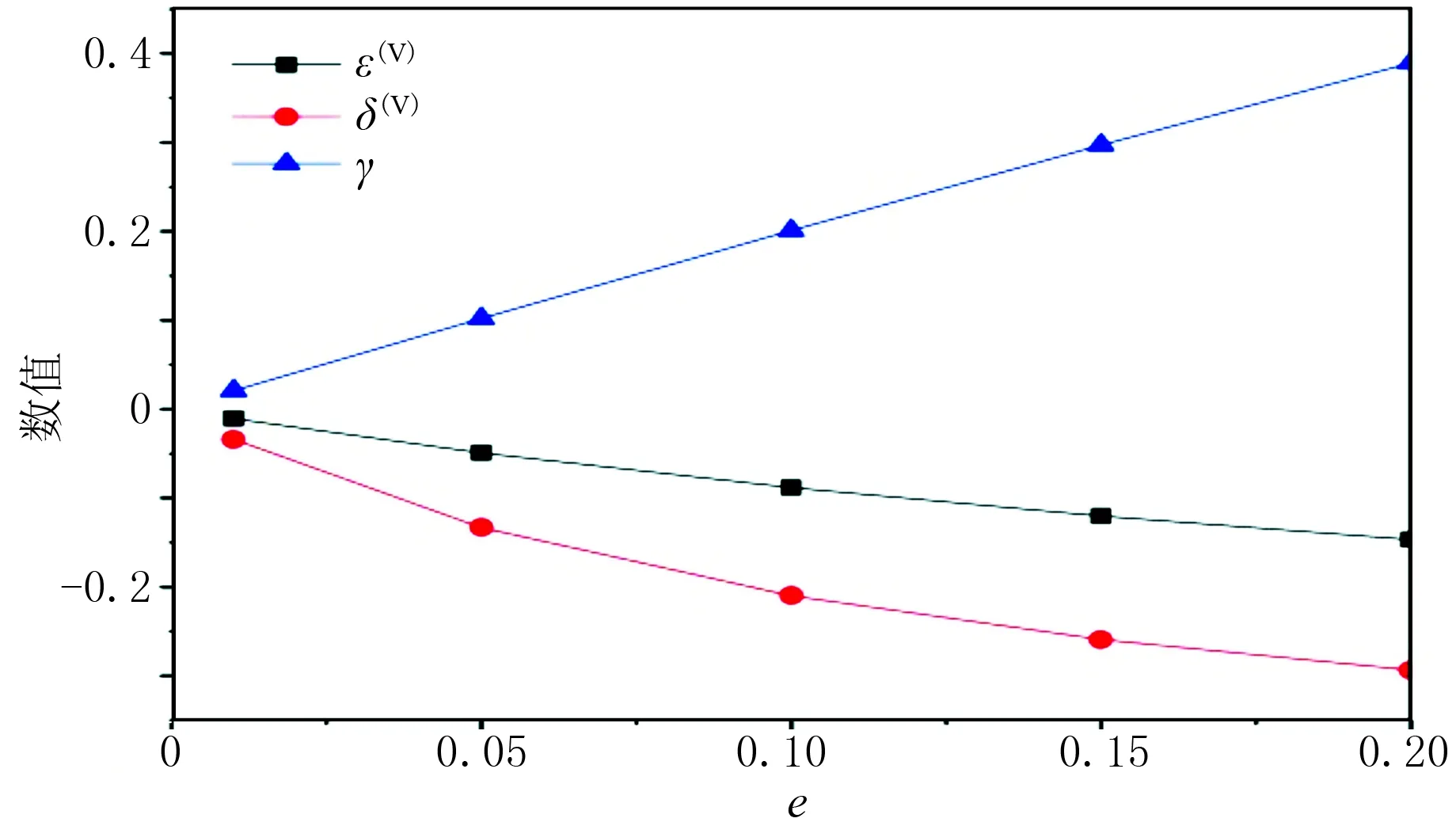
图2 各向异性参数随裂缝密度变化曲线

由图2可知，随着裂缝密度e的增加，γ值显著增大，而ε(V)、δ(V)减小，且后两者变化率更小，说明裂缝密度对快、慢横波速度差异影响最大。

3 AVO响应分析

为了研究HTI介质AVO响应规律，采用Rüger[23]提出的HTI介质反射系数近似公式计算PP、PS1与PS2波的反射系数

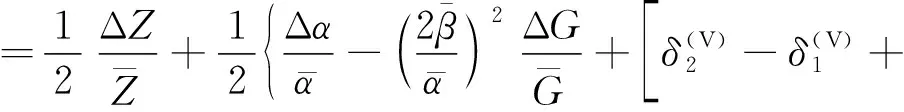
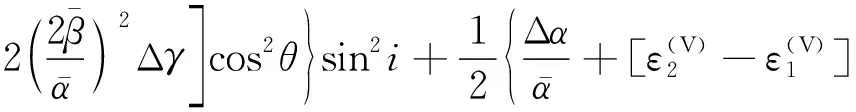
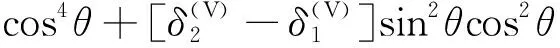
(10)

(11)

(12)

式中：Z为垂向纵波阻抗；G为快横波剪切模量；i为入射角；j为反射角；θ为入射方位角；下标“1”代表上层介质；下标“2”代表下层介质；上划线表示上、下介质参数的均值；“Δ”表示上、下介质参数的差值。式(10)～式(12)引入了描述HTI介质的各向异性参数，适用于含裂缝的致密砂岩的AVO分析。

3.1 AVO特征分析

设计一个两层的模型，其中上层为不含裂缝致密砂岩(e=0)，下层为不同裂缝密度的致密砂岩(表3)。计算的PP、PS1、PS2波的反射系数曲线如图3所示，可见PP波和PS2波的反射系数曲线比PS1波的反射曲线起伏要更剧烈，即PP波和PS2波的反射系数对入射角的变化更敏感。图3a中，PP波反射系数随入射角的增大，表现为先增大后减小；随裂缝密度的增高，PP波反射系数曲线起伏更剧烈；相同入射角时，e=0.2的PP波反射系数的绝对值比低裂缝密度的更大；在入射角为10°～15°、60°～70°时，PP波反射系数曲线过零点。图3b、图3c中的PS1、PS2波反射系数始于同一点(零点)，随着入射角的增大，反射系数先增大后减小；随着裂缝密度增高，曲线起伏更剧烈；相同入射角时，e=0.2的反射系数绝对值更大。PS1波反射系数在入射角为70°附近时发生极性转变，即由正值变成负值；而PS2波反射系数曲线在入射角不到60°就发生极性转变。

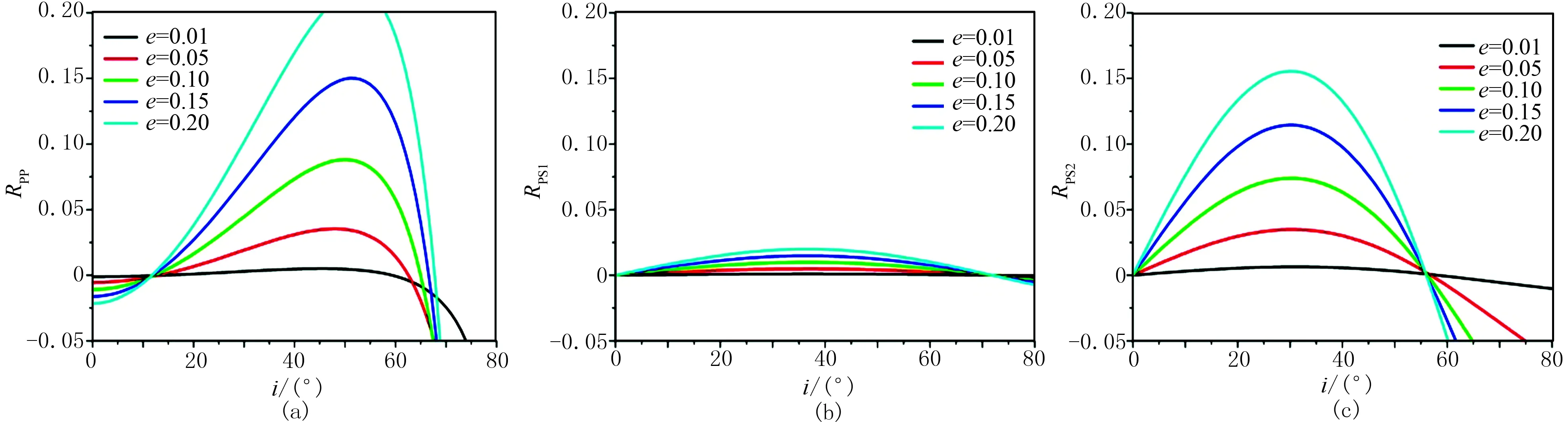
图3 不同裂缝密度时PP波(a)、PS1波(b)和PS2波(c)AVA响应曲线

图4a为各向同性单界面(表4)的PP波反射系数与图3a中的PP波反射系数的差，可知各向异性参数对PP波反射系数影响很大，差值最大可达0.2。对于不同的裂缝密度，PP波反射系数在入射角小于10°时无明显差别，随着入射角的增大，差值增大；在50°附近达到最大，后随入射角增大而减小。图4b为各向同性单界面的PS波(横波不发生分裂，且其值与各向异性介质的PS1波相等)与图3c的PS2

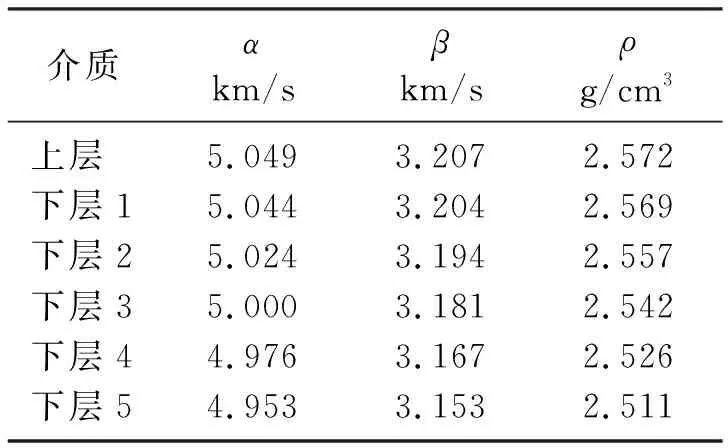
表4 各向同性介质参数

波反射系数的差。由图4b可知，入射角相同时，随着裂缝密度增高，两者的差异越大。当入射角在55°附近时各向同性单界面的PS波反射系数与各向异性介质的PS2波反射系数相近。

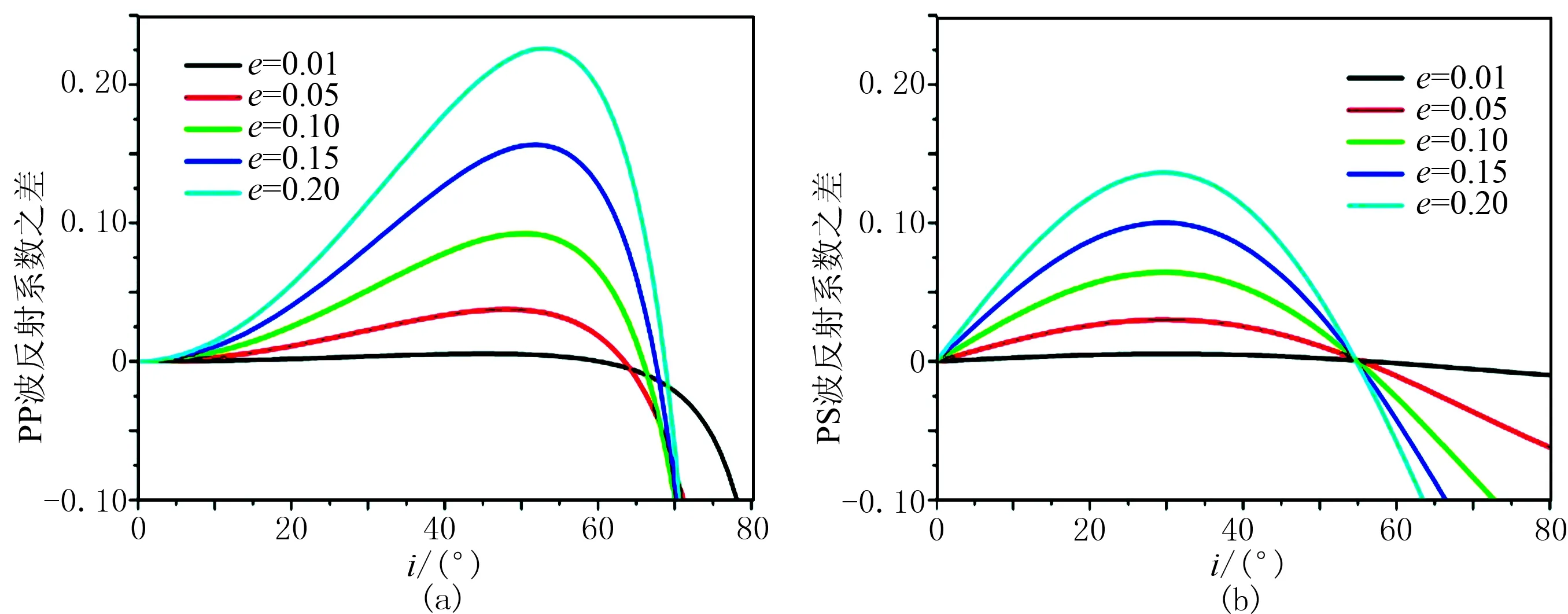
图4 PP波(a)、PS波(b)各向同性与各向异性介质反射系数差值曲线对比

3.2 含裂缝致密砂岩AVA波场对比

用主频为40Hz的雷克子波和图3的反射系数模拟了PP、PS1与PS2波的AVA波场(图5)。由图5可知，随着裂缝密度增高，PP波反射振幅变强，PP波反射发生两次极性反转：第一极性反转点对应的入射角不受裂缝密度影响，第二极性反转点对应的入射角随裂缝密度增高而变大；PS1波反射振幅随着裂缝密度增高而变强，在大入射角时可见一次极性反转，但反转点对应的入射角不受裂缝密度影响；PS2波振幅随裂缝密度的增高而变强，只发生了一次极性反转，且反转点不受裂缝密度影响，但反转点对应的入射角比PS1波小。

图5 下层介质裂缝密度不同时的PP波(左)、PS1波(中)和PS2波(右)AVA波场

4 结论

(1)各向异性参数的计算表明，裂缝密度的增高导致各向异性参数增大，变化最明显的是γ值。PS1波、PS2波反射系数曲线表明，在含裂缝地层的顶界面也会发生横波分裂，且PS2波的反射系数远大于PS1波。

(2)HTI介质与各向同性介质相比，当裂缝密度变化时，入射角小于10°时两者的PP波反射系数无明显差别；当入射角大于10°时，不同裂缝密度的HTI介质与各向同性介质的PP波反射系数会有明显不同，且二者差异随裂缝密度的增高而变大，最大可达0.2。而HTI介质的PS2波与各向同性介质的PS波反射系数除了入射角为0°和55°时非常相近外，随着裂缝密度增高，二者的差异变大。

(3)综合利用PP、PS1和PS2波的反射振幅强弱、极性反转发生位置及其变化规律检测裂缝密度是可行的，其中PP波与PS1波和PS2波极性反转位置变化规律不同。PP波小入射角极性反转的原因有待进一步研究。