利用梯度结构张量检测盐丘与断层

王清振 张金淼 姜秀娣 桑淑云

(中海油研究总院有限责任公司, 北京 100028)

1 引言

多年来，人们基于不同的理论提出了多种不连续性检测方法。目前，断层检测技术是构造解释中必备的一项技术。Bahorich等[1]提出了第一代相干体算法(C1)，这是基于二阶统计量的算法，易于编程实现，简单高效；Marfurt等[2]开发了利用任意数目的地震道估计相干性的算法(C2)，在利用相似性算法估计地层的连续性时，采用一系列试验倾角截取地震道片段构造分析窗，在窗内计算地震波形的相干值，将与最大相干值对应的试验倾角记为局部地层倾角； Gersztenkorn等[3]研发了一种基于特征结构的相干估计算法(C3)，由于特征结构分析可以给出更高的横向分辨率和不连续性度量对比度，因此特征结构相干算法可以改善陡倾地层的连续性度量效果，但是同时会降低平缓地层区域的断层成像效果； Marfurt 等[4]给出一种级联方法解决上述局部倾角估计带来的问题，首先利用相似算法估计局部地层倾角，然后应用具有较大分析窗的中值或均值滤波器平滑得到的倾角数据，以获取可靠的地层倾角估计结果[5,6]，在此基础上采用特征结构相干算法沿地层倾角作相干分析，能得到具有较高横向分辨率的不连续性度量； Israel等[7]提出一种估计局部结构熵的算法(LSE)，具有很高的计算效率，又能较好地抑制噪声，在选择不同大小的分析单元后，可检测不同尺度的不连续性。此外，三维体曲率属性也是不连续性检测的一大热点技术[8-10]，尤其在检测河道及裂缝型油气储层中效果显著[11,12]。但是由于曲率计算过程中要对地震数据求两次微分运算，而微分运算对噪声较为敏感[13-15]，严重影响了曲率属性的实际应用效果。Wang等[16]提出一种高抗噪性三维体曲率分析技术，能够适用于低信噪比资料，特别是在陡倾地层发育区检测结果的假象更少，可真实地反映地下断层及岩性边界等地质信息。王清振等[17]提出了基于高维物理小波变换的不连续性检测技术，能够更好地检测小断层、小河道等地质体边界信息，并且具有较强的抗噪性。

在盐岩剧烈活动地区，在盐的挤压下地层发生严重变形，形成复杂的构造特征，导致断层识别困难，常规的相干和曲率算法很难取得理想的效果。Randen等[18]提出利用图像处理中的梯度结构张量法对三维地震数据的梯度向量场进行平滑滤波，提取有用的地震结构信息。Luo等[19]、问雪等[20]发展了基于梯度结构张量的梯度向量平滑方法，将梯度结构张量构造过程中的三维高斯低通滤波函数替换为由复地震道瞬时能量作为加权值的数据自适应低通滤波方法，可大大提高倾角和方位角估计结果的空间一致性。Wang等[21]给出一种向量翻转迭代滤波法平滑梯度向量场，该方法首先选定参考方向，将所有梯度向量针对参考方向进行翻转，然后对得到的向量场进行均值平滑并且更新参考方向，通过迭代上述步骤取得最终的地层走向估计。这种方法避免了梯度结构张量方法在主特征值不存在时无法准确估计地层走向的问题。

基于前人对梯度结构张量性质的研究，本文提出了一种新的盐丘和断层检测技术——梯度结构张量(GST)不连续性检测技术。首先利用地震数据构造梯度结构张量，然后对梯度结构张量做特征分解，求取其特征值和特征向量，最后利用三个特征值的组合构建出一种混沌度量，从而有效识别复杂构造中的断层及盐丘发育范围。实际数据应用表明，在盐岩剧烈活动地区的断层识别中，与C3、曲率等算法相比，GST方法能够更好地克服由陡倾地层引起的不连续性假象，可清晰地反映真实的断层信息和盐丘发育范围，为盐丘的三维雕刻提供可靠的基础数据。

2 技术原理

GST是分析和描述地震数据中构造特征的一种有效工具。该方法利用梯度矢量描述地质体的倾角和方位，采用梯度张量矩阵的谱分解描述地震数据的构造特征，可有效度量断裂、河道、礁体内部纹理、平行与亚平行结构、倾斜层理、波状层理等地质现象。梯度结构张量Mρ的定义为

(1)

采用标准差为ρ的各向同性高斯核Gρ对梯度向量的各个分量作光滑平均。其中Gρ是三维的标准高斯函数，其形式为

(2)

式中:U为原始地震数据；Uσ为平滑后的地震数据，其中σ为尺度参数，其取值取决于待分析数据的噪声强度，即定义为噪声尺度，可降低梯度数值计算对噪声的敏感度，也建立了梯度结构张量可度量的最小构造尺度；Gσ为尺度参数为σ的各向同性高斯核。标准差ρ的选择取决于构造度量和分析的分辨率，即定义为构造尺度，在ρ的高斯邻域内平滑梯度张量，使其成为一个对称半正定矩阵，提高了结构分析的鲁棒性。

对梯度结构张量Mρ进行矩阵特征分解

(3)

式中：λ1≥λ2≥λ3≥0为Mρ的三个非负特征值；v1,v2,v3为对应的特征向量，它们构成一个局部的正交坐标系，v1表征局部邻域内对比度最大的方向(信号的梯度方向)，v2和v3构成一个垂直于v1的局部平面。Mρ的三个特征值的含义与对应数据体中的空间结构特征关系如表1所示。

据此构建构造混沌度量如下

(4)

基于GST的混沌度量可有效反映局部构造的规则性，且不依赖于振幅变化。即：mchaos→1， 对应于横向不连续性构造；mchaos→0， 对应于反射杂乱不规则区域；mchaos→-1， 对应于规则的层状构造。

为了形象地说明混沌度量与空间结构特征的对应关系，引入一个半球形的盐丘模型，用一组正弦波信号模拟地层反射。盐丘内部为具有杂乱反射特征的不规则区域，盐丘边界为类似于断层、岩性边界等地质特征的线性结构，正弦波信号代表规则的层状构造结构。由模拟结果(图1)可见：盐丘内部杂乱反射特征的GST检测结果为0(图中显示为白色)；规则的层状构造的GST检测结果为-1(图中显示为红色)；岩性边界检测结果则为1(图中显示为黑色)。模型数据说明GST算法可有效地识别三种空间结构类型。

表1 Mρ的三个特征值与空间结构特征对应关系

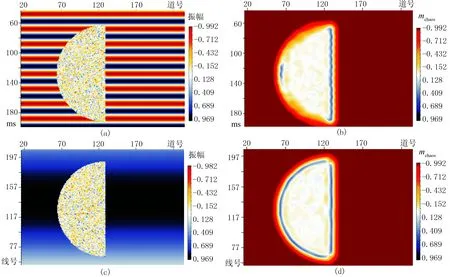
图1 半球形盐丘模型模拟结果

σ、ρ显著影响检测结果的分辨率。图2为不同的σ、ρ取值的半球形盐丘模型GST检测结果时间切片。由图可见：当ρ=4、σ分别取0.5(图2a)、1.0(图2c)和2.0(图2e)时，随着σ增大，检测结果分辨率显著降低； 当σ=0.5、ρ分别取2(图2b)、3(图2d)和5(图2f)时，随着ρ增大，检测结果分辨率降低。在实际工作中σ的取值要考虑地震数据信噪比，即：当信噪比较高时σ要取较小值，可提高检测精度；当信噪比较低时σ要取较大值，以降低噪声的影响，可提高结果的稳定性。对ρ的选取则需要考虑具体的工作目标，即： 当检测大尺度的不连续性信息时，则ρ取较大值；反之当检测小尺度的不连续性信息时，则ρ取较小值。

图2 不同σ、ρ取值的半球形盐丘模型GST检测结果时间切片(128ms)

3 实际应用

利用GST在盐岩发育区进行了测试。图3为A区5835纵测线地震剖面及其C3、GST、最大正曲率检测结果，图4为A区地震数据4000ms时间切片及其C3、GST、最大正曲率检测结果。由图可见：①该区盐岩极为发育且活动剧烈，盐上地层由于受到盐岩活动影响，发生剧烈的扭曲畸变，褶皱广泛发育，地层倾角变化范围为0°～90°，地层的复杂变化导致断层识别困难，仅从剖面上很难直观地解释断层(图3a)；在地震数据时间切片中存在很多闭合圈，也形象地展示了盐岩滑动对地层的剧烈改造作用(图4a)。②由于地层倾角变化剧烈，C3算法无法有效地识别断层，剖面检测结果几乎全是黑色高值区域(图3b)，平面检测结果也不能刻画断层分布和盐丘展布(图4b)。③曲率算法的效果略好，但剖面(图3d)和平面检测结果(图4d)均不能准确地刻画断层聚焦度和盐丘边界，且在平面上由于整体高曲率值范围太大，导致关键边界信息不明显，断层不易识别。④在GST平面检测结果中(图4c)断层清晰可见(红蓝箭头指向)，在GST剖面检测结果中也见断层形迹(图3c)，且GST平面检测结果的黑色杂乱反射区域分布范围(绿色框内)和剖面检测结果的盐岩发育区对应很好，说明GST能有效检测盐岩空间展布范围。但是也可以看到，GST检测结果的分辨率不高，尤其对倾斜断层，断点检测结果与实际结果有一定的偏移量，这是因为在计算地层GST时使用各向同性高斯函数进行平滑，导致分辨率有所下降。

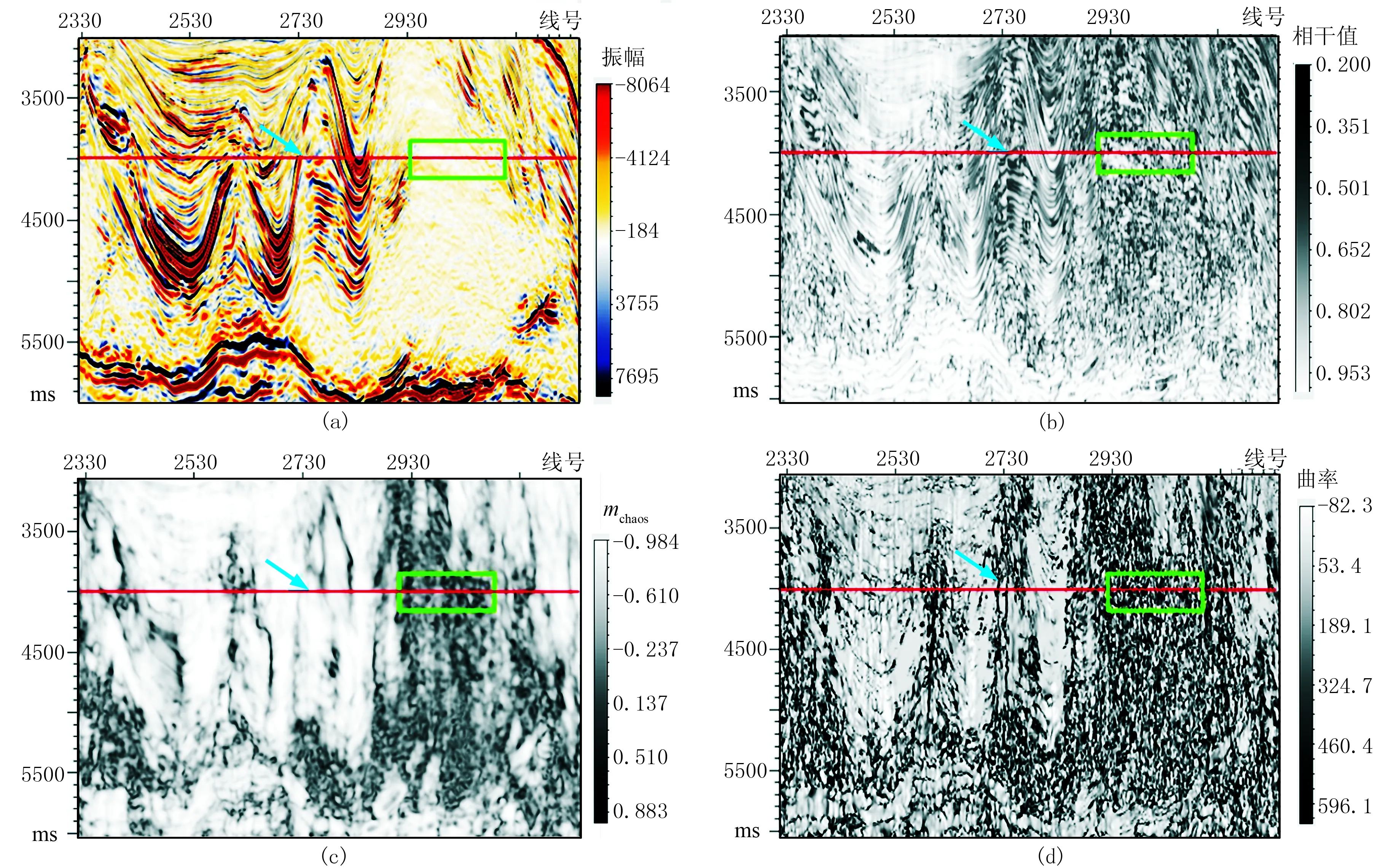
图3 A区5835纵测线地震剖面(a)及其C3(b)、GST(σ=1，ρ=3)(c)、最大正曲率(d)检测结果

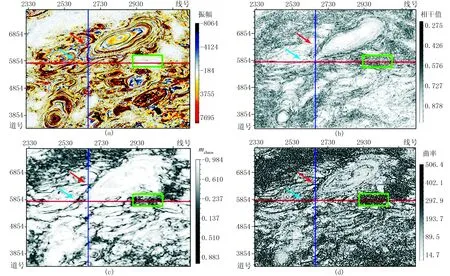
图4 A区地震数据4000ms时间切片(a)及其C3(b)、GST(σ=1，ρ=3)(c)、最大正曲率(d)检测结果

4 结论

在盐岩发育区域，由于盐岩具有易变形、易流动的特性，常常导致地层发生褶皱弯曲，形成极为复杂的构造特征，利用常规方法进行断层和盐边界识别极为困难。由于地层倾角分布范围很广，根据倾角难以区分层位和断层，常常导致异常检测结果。为此，本文提出了一种基于地震资料梯度结构张量的盐丘和断层检测技术，利用梯度结构张量可很好地反映不同构造特征，将三个特征向量进行有机组合构建一种混沌度量，可屏蔽弯曲地层的影响，有效识别断层和盐丘展布范围。实际资料应用结果证实，该方法较第三代相干、曲率等常规方法更能适应盐岩剧烈活动区的盐丘与断层识别，检测的断层更聚焦，盐丘边界更准确。尚须指出，由于计算地层梯度结构张量利用各向同性高斯函数进行平滑，因此检测结果的分辨率不高，尤其对倾斜断层，断点检测结果与实际结果有一定的偏移量。今后可以考虑根据局部构造特征构建基于各向异性介质的梯度结构张量，对初始梯度矩阵场做平均，以提高检测结果的分辨率。