应用网格走时的射线路径计算方法

魏脯力 孙建国 孟祥羽

(吉林大学地球探测科学与技术学院，吉林长春 130026)

1 引言

射线路径和射线走时是描述波场传播运动学特征的两个基本概念[1]，均来自于关于波场传播的高频渐近理论。其中：射线路径给出高频波场的传播路径，是纯几何量； 射线走时描述高频波场沿射线的传播时间，具有明确的物理含义。根据高频渐近波动理论，走时满足程函方程，射线满足程函方程的特征线方程[2]。这意味着，走时和射线路径均来自于同一个非线性偏微分方程，即程函方程。因此，通过解程函方程，既可得到射线走时，也可得到射线路径。如果利用关于非线性偏微分方程的特征线法首先求出射线路径，则可通过对慢度沿射线路径的积分得到走时。这是传统射线追踪的基本内容。如果直接利用数值方法，例如有限差分法[3，4]，则只能得到走时，而不能得到射线路径。这是现代计算走时的基本途径。为了解决射线路径的计算问题，需在得到全部计算网格点上的走时之后利用射线路径与走时场梯度之间的关系计算射线路径[5，6]。这是现代射线走时和射线路径计算的基本内容。

由于程函方程源自于几何射线级数理论，所以基于程函方程数值解的网格走时计算方法[7-15]只能给出初至波走时，从而与其对应的射线路径计算结果也只能是初至波射线的路径。为解决多种波型的走时和射线路径(多值走时和多路径射线)的计算问题，一种途径是将对应的多值走时分解成不同的单值走时求解，如Benamou[16]根据射线追踪结果将计算区域划分为一系列初至波走时计算区域，它们的重叠部分则对应着多值走时或多路径的位置。另外，可根据走时场的互易性计算多值走时与多路径射线。正是基于这一事实，Rawlinson等[17]提出了子射线法(Raylet method)。根据定义，子射线为局部射线线段。在具体计算过程中，子射线的起点被视为是一个新源点，而其终点被视为是一新的接收点。根据Fermat原理，子射线在其起点和终点之间具有极小走时。因此，只要子射线的起点与终点之间距离足够小，就可计算出与全部绕射和散射波所对应的射线。

在Rawlinson等[17]的子射线法中，为计算多路径射线，需要计算地下每一网格点到源点和接收点的走时之和，然后拾取总走时场的极值确定射线路径。因为实际射线路径附近的总走时本身变化缓慢，所以所寻找的极值点大多位于非网格点上。这给实际计算带来了一定的难度和问题。针对这个问题，提出了利用源点到给定点和接收点到给定点的总走时的(横向或纵向)导数计算射线路径。由于极值点对应着一阶导数的零点，所以问题就转化为如何寻找总走时(横向或纵向)一阶导数的零点问题。为了精确地确定一阶导数零点的位置，引入反插值法[18]。

本文首先简要回顾Rawlinson等[17]提出的子射线法，然后详述基于反插值法的子射线法改进方案及其实现步骤，最后给出若干数值试验结果。

2 方法原理

2.1 子射线法原理

借助于图1[17]，介绍“子射线”概念。假设源点S和接收点R之间存在3条射线路径，按照旅行时的大小将这些射线分别称为初至射线，“二至”射线和“三至”射线。在图1中，用线段示意性地展示了“三至”射线的几个传播阶段： 第一条直线给出了射线由源点到接收点发生两处波型转换的过程，即由最初S1段对应的初至波，到S2段对应的“二至”波，再到后来S3段的“三至”波。根据互易性原理，射线由接收点到源点会经历相同的演化过程，即图中第二条直线所给出的R1到R2，再到R3。现在综合考虑源点到接收点及接收点到源点这两个演化过程，对应的可将该“三至”射线划分为图中第三条直线展示的几部分。可知S1R1段射线对应的源点走时场和接收点走时场均属于初至波，将其称为一阶子射线，而S1R2和S2R1段射线对应的接收点走时场或源点走时场为“二至”波，称这样的射线段为二阶子射线。依此类推，S1R3和S3R1被称为三阶子射线。因此该“三至”射线可看作由不同阶的子射线构成。上述定义中假设源点与接收点之间存在3条射线路径，实际上任意条数射线都可得到同样的定义。

根据文献[17]，子射线法是利用网格走时完成局部多值走时的。首先，利用有限差分法得到计算区域内每一网格点到源点和接收点的走时并将其相加，得到所计算区域的局部总走时场。然后，求取总走时场的局部极值点并将其作为最终的射线点。因此，子射线法得到的射线路径对应着上文中定义的一阶子射线。当两点之间只有一条射线路径时，其求解得到的一阶子射线即为全域性的最短时间射线路径。

图1 子射线的定义[17]

2.2 反插值法与射线点求取

假设函数f(x)的离散节点为

(xi,f(xi))i=0,1,2,…,n

则插值问题就是计算x0,x1,x2,…,xn之间的x点处f(x)的近似值，一般通过构造插值函数的方法实现。根据不同的构造方法，可分为Lagrange、Newton和Hermite等不同插值法。

与此相反，反插值问题[18]则是计算f(x)=c时x的近似值，其中c为f(x0),f(x1),f(x2),…,f(xn)之间的值。反插值有两种实现方式：一种是利用f(x)的插值多项式，一般为低阶多项式；另一种则是在f(x)存在反函数f-1(x)的情况下，构造f-1(x)的插值多项式。当f-1(x)存在时，有

x=f-1(c)

反插值就是求反函数f-1(x)在c处的近似值。当c=0时，反插值即为求方程f(x)=0的近似解。因为射线路径对应走时的极小值，即对应走时(横向或纵向)一阶导数的零点，所以借助反插值可较精确地求取射线点位置。

2.3 算法实现

子射线法的计算效率与网格走时计算方法有关。为了快速地计算出局部走时场，采用了基于快速推进迎风线性插值法的走时计算策略[12-15]。

实际计算表明，寻找总走时(源点到给定点走时与接收点到给定点走时之和)的极值确定射线路径具有两个明显的问题：射线附近的总走时场变化缓慢，因此需要较为苛刻的走时计算精度；非网格节点上的极值点计算比较困难。为解决这两个问题，采用局部总走时场的(横向或纵向)导数确定射线路径。具体的算法由下列4个步骤组成。

(1)总走时场计算

首先将地下速度空间划分为正方形网格，然后利用基于快速推进迎风线性插值法的走时计算策略分别计算源点到每一网格点和接收点到每一个网格点的初至波走时。对每一个网格点的这两个走时值求和得到总走时。考虑到射线理论的高频假设和后续导数计算的需要，对速度模型进行一定光滑是有必要的[19，20]。

(2)总走时场的一阶导数计算

对总走时场求导可以看作是计算总走时场的横向导数与纵向导数，因为最终的目的是拾取极值点构成射线路径。当射线路径非近水平时，只拾取横向导数为零的点往往是足够的。下面不加证明地直接给出3点导数算子和5点导数算子[21]公式

(1)

(2)

式中： Δh为网格间距；τ为总走时；i-2,i-1,i,i+1,i+2分别对应相邻的横向网格节点；q为总走时场的横向导数。通过式(1)或式(2)，就可得到总走时场在每一个网格点处的横向导数。

(3)一阶子射线计算

假设所求的射线路径非近水平，则可通过拾取总走时场横向导数为零的点构成所求的射线路径，一种简单的实现方式是利用反插值随深度计算导数为零的点。

图2为计算射线路径的方法示意图。其中实线表示待求的射线路径，且已知量为每个网格点处的横向导数值。将计算网格横、纵向从零开始编号，i和j分别对应当前计算位置的横、纵向编号。因为射线点是总走时场的极值点，所以此时射线点处的横向导数为零，其两侧相邻网格点处的横向导数异号，即

qi·qi+1<0

(3)

式中q表示总走时场的横向导数。

假设射线点附近的横向导数线性变化，则可由其两侧相邻网格点处的横向导数值反插值得到射线点的横向和纵向位置

(4)

z0=jΔh

(5)

在式(4)中，当qi=0时，x0=iΔh；当qi+1=0，x0=(i+1)Δh。即式(4)对于网格点上的射线点同样满足，不过此时的判定条件应改为

qi·qi+1≤0

(6)

利用上述公式，该算法可概述为：从源点深度开始，利用式(6)、式(4)和式(5)得到当前深度射线点(多路径时对应多个射线点)的坐标，然后进行下一深度的计算，直到检波点深度为止。

图2 射线点计算示意图

从图2可看到，通过线性反插值计算得到的射线路径(虚线)其实是对准确射线路径(实线)的一种近似。考虑多路径的可能性，上述算法得到的实质上是一阶子射线的计算结果。

(4)高阶子射线计算

当射线存在多路径时，上述算法只能完整地计算出最短时间射线路径，其他射线路径只有一阶子射线的计算结果。若想完整地计算出整条射线路径，只需要分别计算得到源点到子射线端点和接收点到子射线端点的射线部分即可，也就是计算其他阶的子射线。具体实现途径只需要重复上述的步骤(1)～(3)，直到计算出整条射线路径为止。

上述算法针对于非近水平的射线路径计算，只利用了总走时场的横向导数；实际上对于近水平的射线路径计算，同理可以利用总走时场的纵向导数得到，或者对于一些复杂的射线路径计算，综合利用横、纵向导数可能会更便于计算。

3 误差分析

3.1 均匀介质

均匀介质中的射线路径为直线，为了说明计算网格尺度与导数算子长度对算法的影响特点，将算法应用于图3所示的速度为2000m/s的均匀介质中。模型长度和深度分别为8、6km，源点位置为(4km，0)，首先采用10m的网格常数和3点导数算子，分别计算了源点到不同接收点位置的射线路径，图3中虚线对应计算结果，作为对比，图中用实线绘出了精确的射线路径。直观来看，两者具有很高的一致性。为了定量表示计算偏差，引入绝对误差均值的定义。

因为采用定深度的计算方式，所以只需讨论射线路径横向位置的计算误差，定义计算结果相对于精确结果的绝对误差均值为

(7)

图3 均匀介质中的射线路径

式中：j=0,1,2,…,J-1，对应纵向网格编号，即对应不同的计算深度；xj和x0j分别为相应深度的计算结果与精确结果，因此绝对误差均值定量表示了计算得到的射线路径相对于精确射线路径的偏差。

针对图3中的3条射线路径A、B和C，进一步采用5m的网格常数和5点导数算子进行计算，对应的计算误差如表1所示。

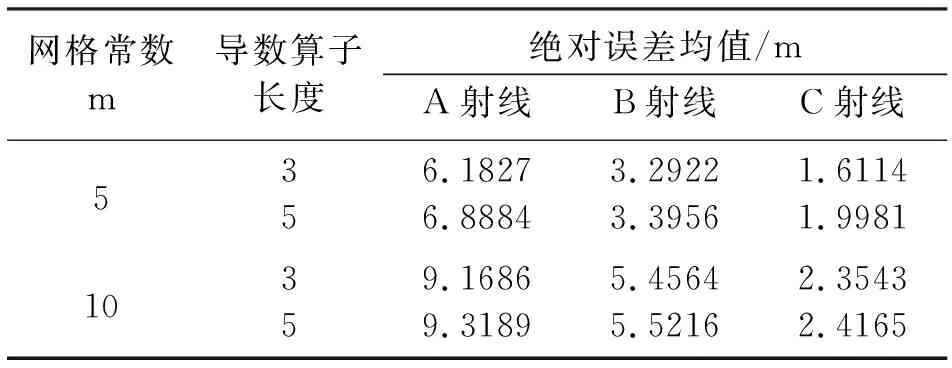
表1 不同网格常数与导数算子长度下的射线路径误差

从表1可知：较小计算网格尺度对应较高计算精度，但导数算子长度并不是越长精度越高；相反，较小导数算子长度对应较高计算精度，这主要是因为表1中的误差其实是网格常数与导数算子长度的一种综合效应，而网格常数的影响要明显大于导数算子长度。图4详细给出了3条射线(A、B、C)在不同深度处的横向位置计算误差(考虑了误差的正负性)，图中实线对应10m的计算网格，虚线对应5m的计算网格，因为导数算子长度的影响甚微，图中并未加以区别。通过图4可见，随着网格间距变小，射线的光滑性显著降低，所以在实际计算中应综合考虑计算精度与射线光滑性的影响。

图4 均匀介质下深度域的射线(A、B、C)的横坐标误差

3.2 垂向梯度介质

当速度只随深度变化，且变化梯度为常数时，可推导出射线路径横向位置随深度变化关系式[22]

(8)

式中： (x0,z0)为源点坐标； (x,z)为射线上任意点坐标；v0为源点所在水平面上的速度；p为射线参数，在横向速度不变的情况下，即为源点旅行走时场的横向导数；β对应速度梯度，即

v(z)=v0(1+βz)

(9)

为了得到解析结果，首先需得知射线参数p(或源点走时场的横向导数)的大小。因为基于快速推进迎风线性插值的网格走时计算方法在远离源点的位置误差很小[9]，所以可近似认为由其求导得到的横向导数是精确的。

如图5所示，垂向梯度模型的长度和深度分别为8、6km，地表速度为1500m/s，速度梯度为0.8s-1。数值计算中，源点位于(4km，0)，计算网格间距10m，分别计算了图5所示的A、B和C共3条射线路径，虚线对应计算结果，实线对应精确的解析结果。同样可看到，数值结果与解析结果具有很高的一致性。

图5 垂向梯度模型中的射线路径

网格间距m导数算子长度绝对误差均值/mA射线B射线C射线1034.428013.620610.808954.514213.669310.8980

表2分别给出了3点导数算子和5点导数算子下的绝对误差均值，与均匀介质下的相同，较小的导数算子长度对应着较高的计算精度。同时，图6具体给出了不同深度下数值计算偏差。图中A射线在较深处误差较大，这是因为射线路径近水平引起横向反插值出现较大偏差所致。

图6 垂向梯度介质下三条射线的横坐标误差

3.3 横向变速介质

为了测试本文算法对横向速度变化的适应能力，采用如图7a所示的横向变速模型，讨论当射线路径通过不同程度的横向速度变化时，本文算法与常规运动学射线追踪结果的计算偏差的相对大小。

在图7b中，网格常数为10m，源点位置是(4km，0)。图中实线给出了常规运动学射线追踪结果，射线出射角度范围是-12°～12°，角度间隔为2°。从这些射线路径上挑选一点(图中A～F)，利用本文算法计算其到源点之间射线路径，计算结果用虚线展示。同时，表3定量给出了本文算法相对于常规运动学射线追踪的计算误差，需说明的是图8中G射线为垂直入射，两种方法的计算都是精确的。

与常规运动学射线追踪结果较好的一致性可说明，本文算法对于横向速度的变化具有很强的适应能力。

图7 横向变速模型(a)及其射线路径(b)

4 计算实例

4.1 多路径计算

图8a为一个低速球体模型，模型的长度和深度均为8km。待计算射线路径对应的源点位置为(4.00km，0.50km)，接收点位置为(3.62km，6.38km)。该图中实线给出了经典试射法计算结果，可见有三条射线路径连接源点和接收点，分别记为A、B、C，那么通过本文算法能否给出这3条射线路径的计算结果？

采用10m的网格常数与3点导数算子进行计算，图8a 中用虚线给出了计算得到的一阶子射线，除了完整计算出初至波射线A以外，算法还得到了射线B和射线C的一部分。为了完整计算出射线B与射线C， 采用分级次计算的策略，即分别计算一阶子射线端点到源点和接收点之间的射线路径。图8b用灰色虚线给出了射线B其他部分计算结果，同理图8c对应射线C。至此，得到A、B、C三条射线路径的完整计算，其与经典试射法结果几乎完全重合，也说明了该多路径算法的有效性与准确性。

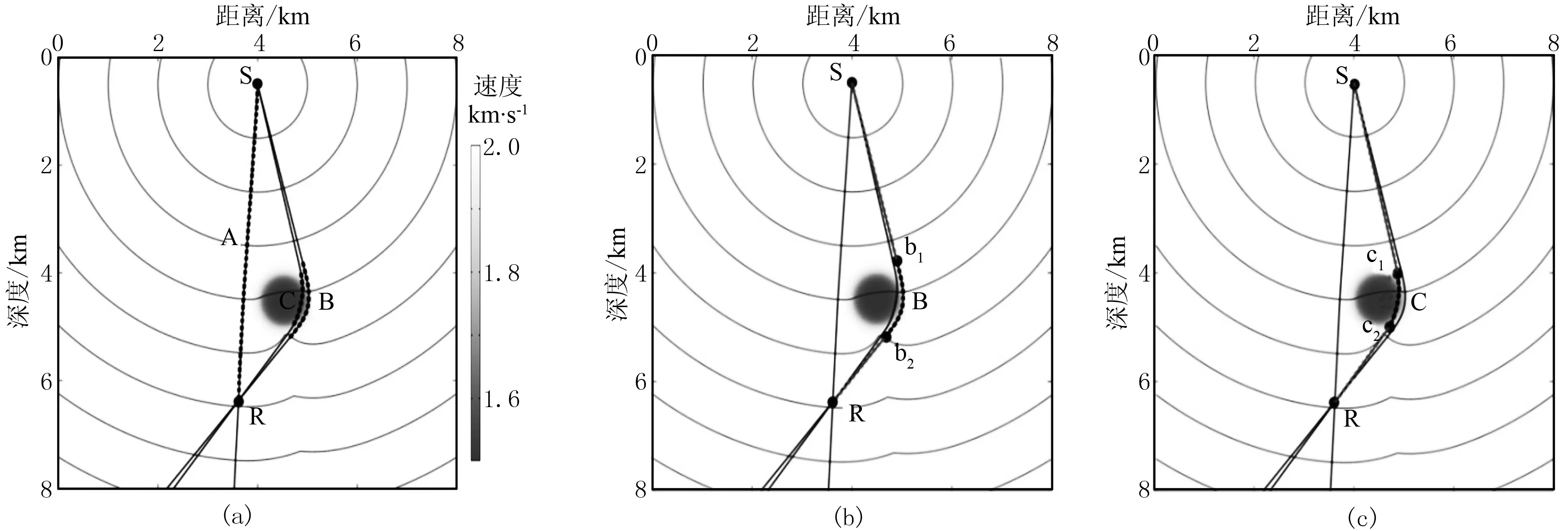
图8 低速体模型中的射线路径(a)、二阶及以上子射线(b，c)计算结果

4.2 Marmousi模型

为了测试本文算法在复杂介质中的应用效果，对比了常规运动学射线追踪在复杂的Marmousi模型下的计算结果。

图9a所示为Marmousi模型的一部分，其长度和深度分别为4.88、6.00km。在射线路径的计算中，采用10m的网格常数将速度模型网格化，同时根据射线理论的高频假设与导数计算的需要，对速度模型进行适当光滑是有必要的。图9b中用实线给出了常规运动学射线追踪的结果，其中源点位置为(3km，0)，射线出射角度范围是-20°～20°，出射角度间隔为2°，因此共追踪到了11条射线路径。为了将本文算法与常规运动学射线追踪结果进行对比，对应这11条射线路径，分别计算了射线路径上一点(图9b中A～K)到源点之间的射线路径，计算结果被用虚线表示在图9b中，可看到其与常规运动学射线追踪结果几乎完全重合，也说明了算法在复杂地质条件下同样具有很好的应用效果。

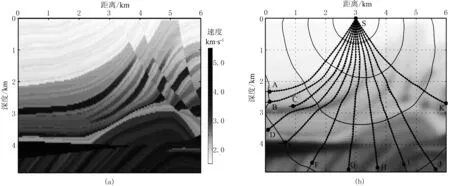
图9 Marmousi模型(a)及其射线路径(b)

5 讨论

根据程函方程，沿着射线路径走时梯度矢量的长度等于慢度。因此，这里所指的走时梯度不是沿着射线路径的走时梯度，而是在给定接收点附近与相应射线场相对应的走时梯度。原则上，只要不是沿着射线路径求导，则利用任意方向上的导数均可以找到走时场的局部极值。

此外，在利用反插值法计算射线点时，曾假设射线点附近的总走时导数呈线性变化。理论上，这个假设不是必须的。事实上，可以考虑其他局部走时变化模型，以改进子射线的光滑性。

6 结论

根据子射线法的基本原理，通过引入反插值法，并结合基于快速推进迎风线性插值法的走时计算策略提出了一种计算多路径射线的改进子射线法。数值计算表明：基于反插值法的子射线计算精度主要依赖于计算网格尺度。较小的网格常数具有较小的射线路径偏差。然而，随着网格的逐渐变小，所得到的射线路径也逐渐变得不光滑，且计算时间也成倍增加。因此，在实际计算中应综合考虑各种因素来选取最佳网格常数。此外，数值计算表明：在实际计算时应尽量选择较短的求导算子。