一类非完整多机器人跟踪控制

◎杨光艳　李　星　李天琪

(中国地质大学(武汉)数学与物理学院，湖北　武汉　430074)

一、引　言

移动机器人作为机器人学中一个重要组成部分，在日常生活中逐步发挥自身优势，使其在人们的日常生活中变得越来越不可缺少.随着科学技术的进步和人类日益精确的分工制度，人类已不满足于对单一机器人的控制，而是更加倾向于对团体机器人即多机器人的跟踪控制[1].轨迹跟踪控制问题是非完整移动机器人在运动控制研究中的重要课题之一[2].循环追踪策略方法首先设计模仿生物有机体的行为，如，狗、蚂蚁等，他们通常被称为“虫类”的问题.文献[3]研究了蚂蚁模型循环追踪行为，板球模型和青蛙模型的离散时间模型和其他可能形成的演化.文献[4]中提出：具有弹性控制增益的线性循环追踪法，并表明代理的收敛点可以通过分配不同的控制增益来实现控制.文献[5]概括出：循环追踪中的独轮车为在该组中每个代理提供不同速度和控制增益，并为平衡形成的存在提供必要条件.

本文论述了基于一个排的独轮车的控制设计和提出一个循环追踪的新分析.本文的动机是为一组环形耦合独轮车开发一个能够保证系统具有一定的全局行为的系统控制律.本文利用基于投影的循环追踪控制律来对小车的路径进行跟踪.此外，不同于Marshall等人[6]使用的Routh-Hurwitz-like标准，我们利用平衡多边形的稳定性，通过一个复杂特性多项式的根轨迹进行严格的分析.并最终得到：有2个平衡多边形是渐进稳定的，车辆最终收敛到匀速圆周运动，并根据车辆标签按照顺时针或逆时针方向均匀地分布在一个圆周上.

二、跟踪模型简介

(一)跟踪模型的建模分析

坐标系通常分为三类：绝对坐标、相对坐标、极坐标三类.在坐标的选取中，为了编程和操作方便，这里我们采用相对坐标.

本文考虑unicycle模型：

(1)

其中[xi，yi]T∈R2，表示车辆的质心在平面上的位置；θi∈R，表示车辆的行进方向；ui=[xi，yi]T∈R2，表示ui受到输入变量线速度vi和角速度ωi的控制；qi=[xi，yi，θi]T，表示车辆i的位置或姿势.

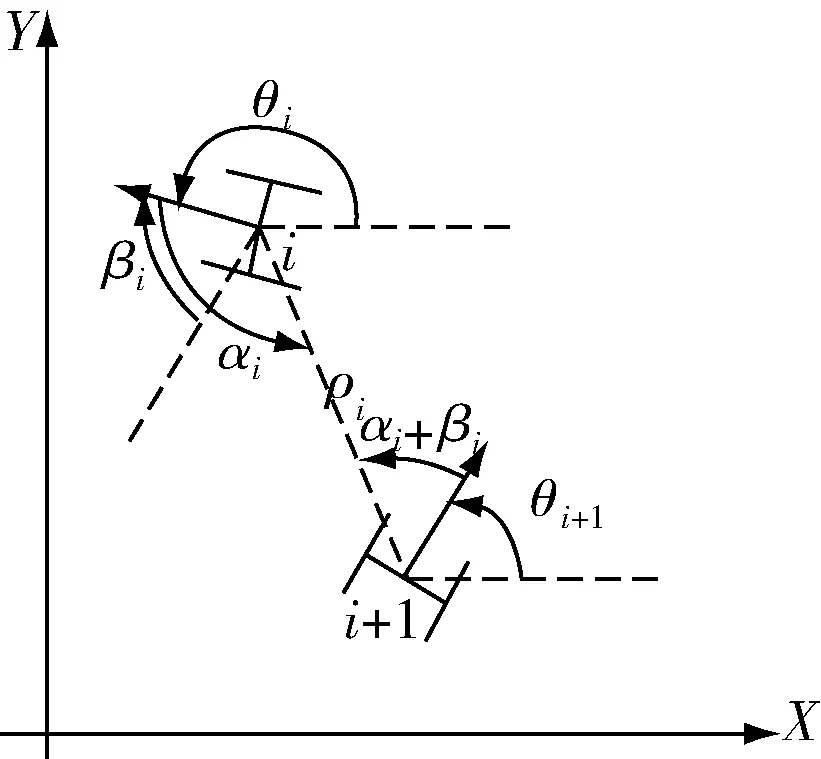
图1　小车之间的位置关系

为了便于分析，我们考虑了相对坐标.ρi表示车辆i和车辆i+1之间的距离；αi表示车辆i的前进方向与ρi之间的角度；βi表示两车各自前进方向与x轴的夹角的角度差减去π的值(即：βi=(θi-θi+1)-π).

(二)循环跟踪模型简介

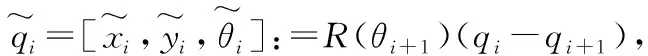
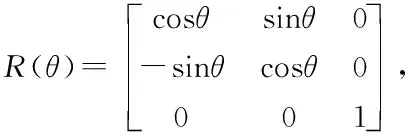
(2)

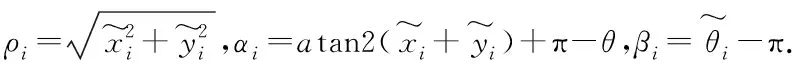
三、跟踪控制方案

(一)循环跟踪控制器设计

接下来，我们提出一个基于投影的控制律，车辆i的线速度和角速度根据车辆i+1相对于车辆i的相对坐标进行按比例分配(图2).就是：

vi=k1ρicosαi和ωi=k2ρisinαi.

(3)

其中k1和k2是控制变量；不失一般性，我们让k1=1和k2=1.

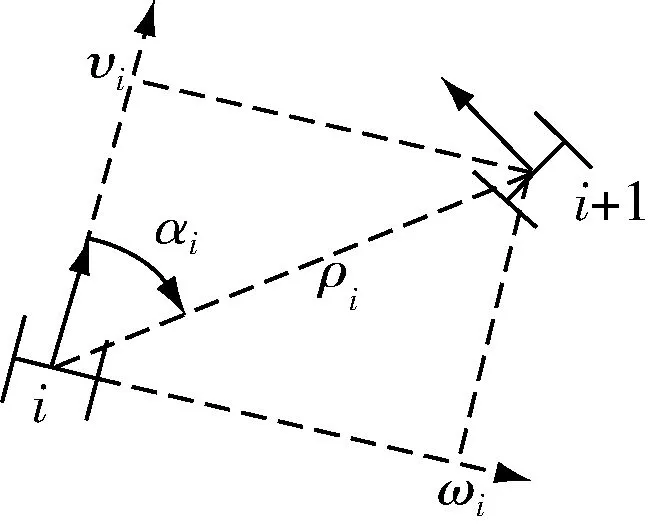
图2　以车辆i的坐标原点的情况下，小车之间的位置关系

(二)有界性分析

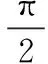
根据已知，我们可以得到：

为了让系统更加简洁，我们定义：

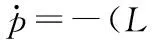
(4)

其中，I2是2×2的单位矩阵，L是n×n的循环矩阵

(三)均衡多边形

设ξi=[ρiαiβi]T，我们把每个子系统作为

(5)

当我们以车辆1的位置为坐标原点时，并根据车辆1的前进方向为导向，可得到车辆2的位置信息，依次这样下去，我们可以得到：

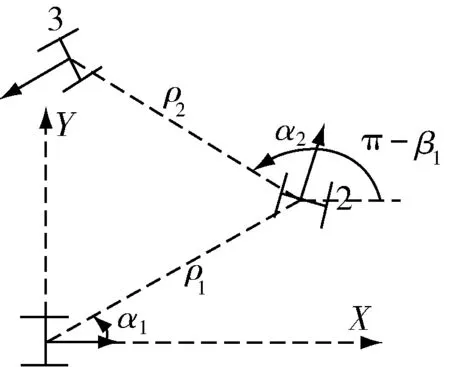
图3　以小车1的位置为原点的位置关系

g1(ξ)=ρ1sinα1+ρ2sin(α2+π-β1)+…+ρnsin(αn+(n-1)π-β1-β2-…-βn-1)=0，

g2(ξ)=ρ1cosα1+ρ2cos(α2+π-β1)+…+ρncos(αn+(n-1)π-β1-β2-…-βn-1)=0.

g1(ξ)=0和g2(ξ)=0分别代表x轴和y轴的约束条件.

另一方面，从(2)中我们可以得到：

(四)稳定性分析

下面讨论每个平衡多边形的稳定性.

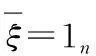
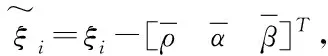
(6)

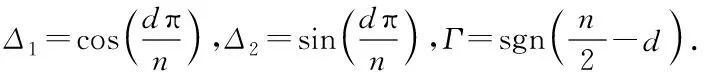
四、仿　真

在本小节中，利用了MATLAB进行了仿真，并针对实验结果进行了认真的分析.

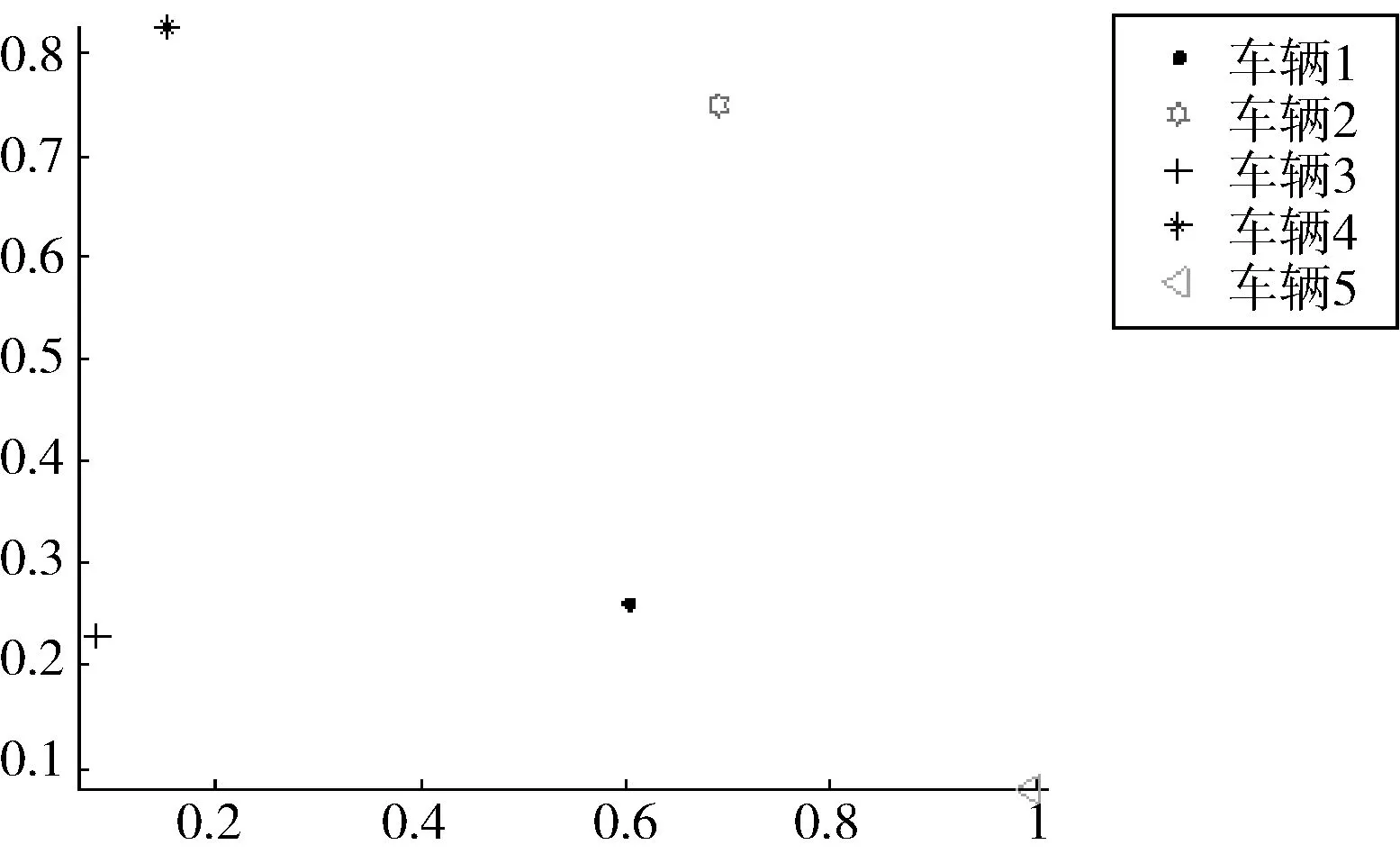
图4　t=0 s

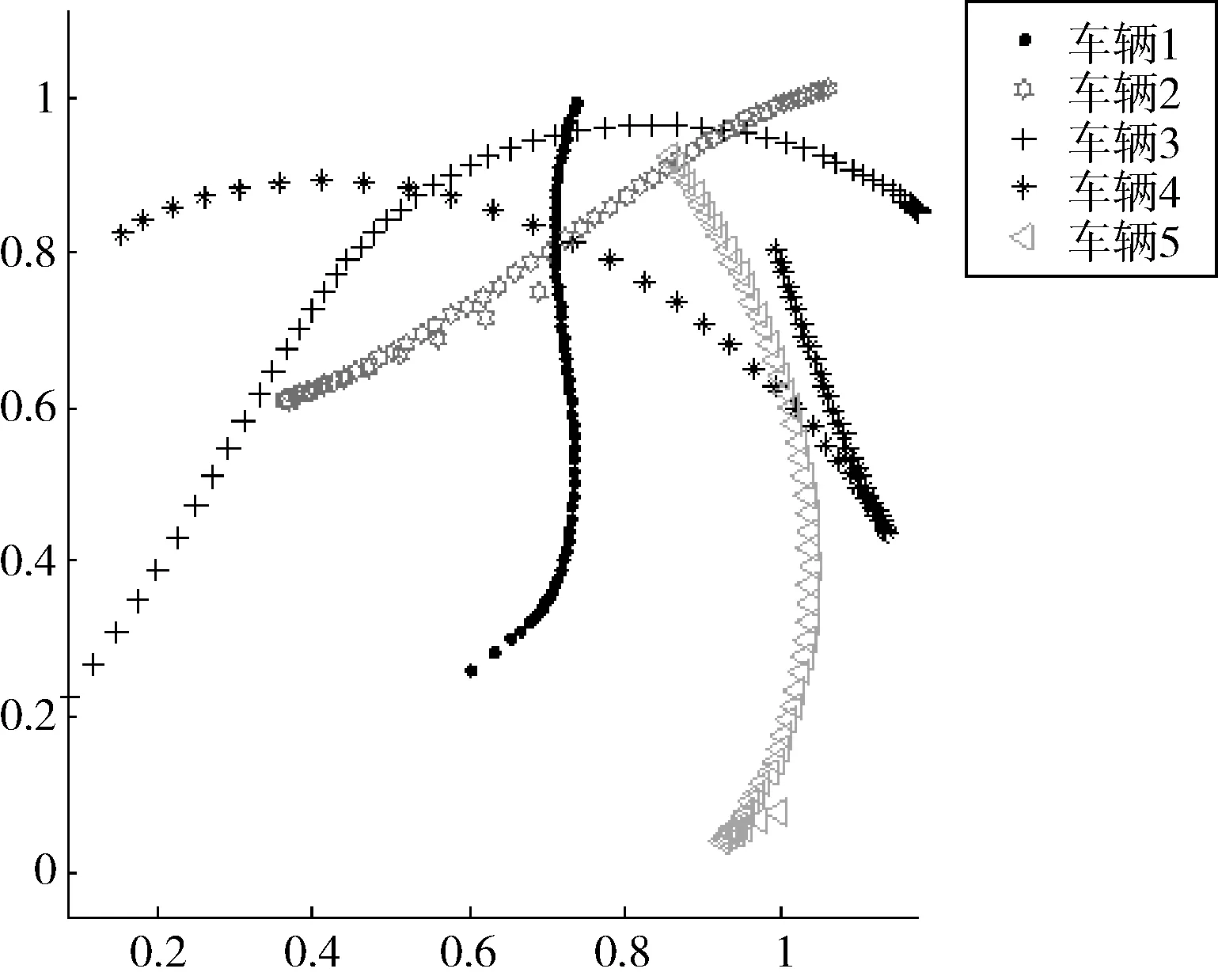
图5　t=10 min

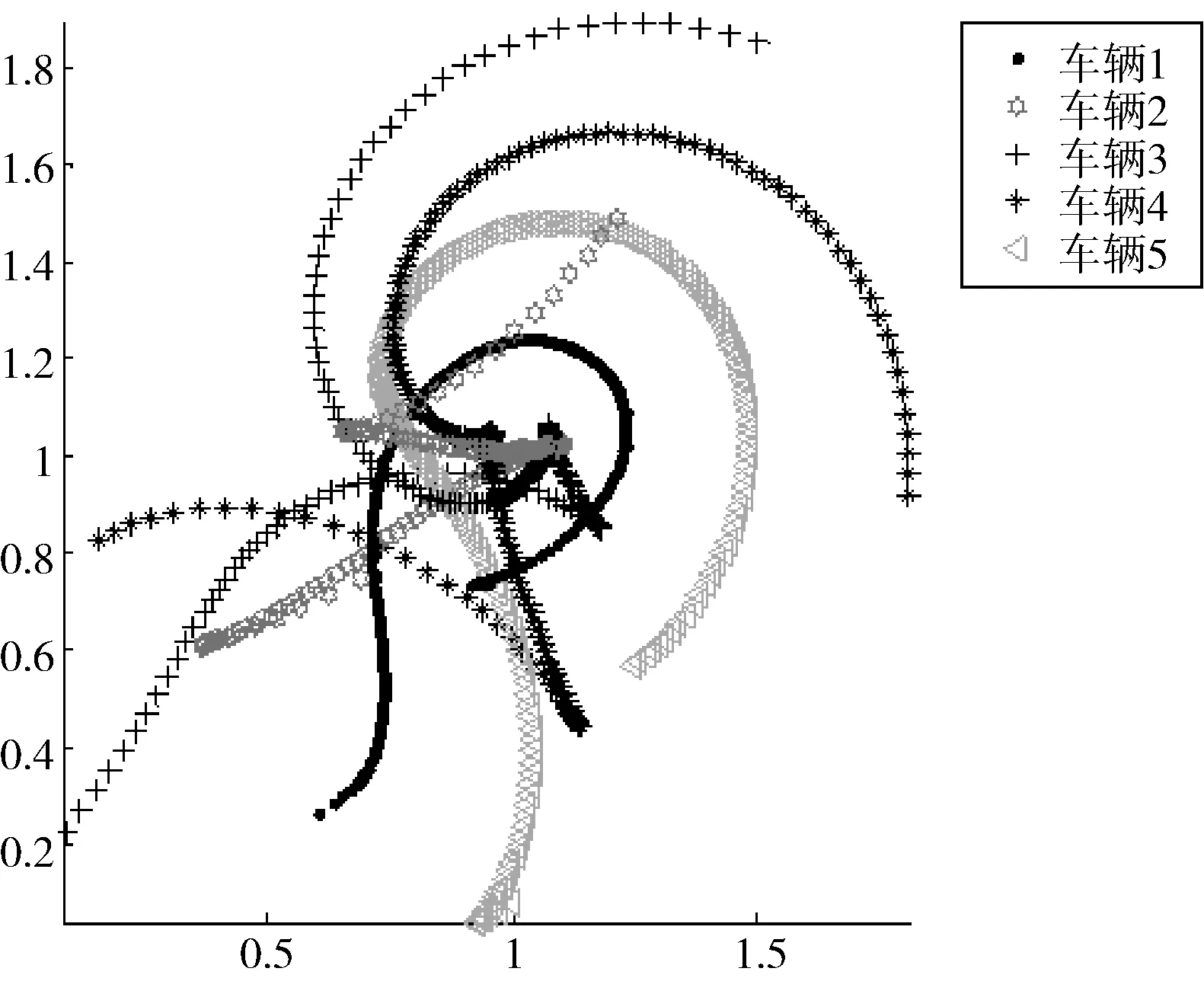
图6　t=15 min

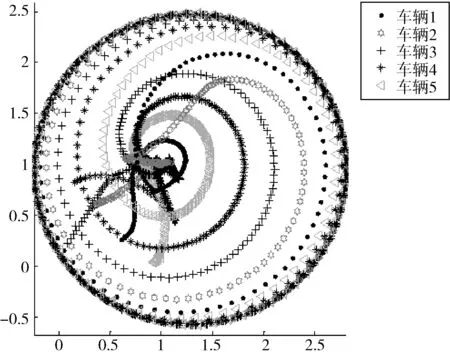
图7　t=20 min

该状态下，当t=0 s时，系统会随机分配小车位置；由于小车位置的随机性，小车运动方向会首选五点之间所连成的多边形的质心方向移动(见t=10 min时刻)，汇聚在一起后，为了达到循环跟踪效果，小车之间会经过相互之间的信息传递，向能够形成的稳定多边形的方向移动，继而会出现由点向边发散的情况(见t=15 min时刻)；经不断试探与探索，会经螺旋形轨道达到稳定状态见(见t=20 min时刻).

五、结　论

本论文中针对非完整多机器人的跟踪控制这一研究课题，利用了一个新的循环跟踪方案.组内的小车之间的交互以合作行为出现，并最终会以恒定的速度和固定的相对间距在一个圆圈内运动.这个控制方案根据伪线性化技术可确保最终的车辆轨迹的有界性；并通过一个复杂特征多项式的根轨迹分析证明了平衡多边形的稳定性和收敛性.本文使用的新方案与其他车辆可能会发散到无穷大的循环追踪控制方案相比，在此方案中车辆的跟踪轨迹会随着车辆总数的增加，能够形成更加稳定的平衡多边形.