“生态课堂”“探”为径

◎孙　永

(江苏省睢宁高级中学南校区，江苏　睢宁　221200)

“生态课堂”突显“生态”两字，是指在教师适时引导，学生自主探究情况下顺其自然地体会知识的发生，发展和形成过程，提升对知识的感性认识和理性认识，达到“随风潜入夜，润物细无声”的最高获知境界的课堂.怎样实施“生态课堂”的教学？实施“生态课堂”教学的有效策略是什么？笔者结合面对全县高中数学教师开设的一节“二项式定理”公开课的一些教学片段，赋予刍议，与同行共勉.

一、创设情境教学，激发学生探究的兴趣

所谓情境教学，是指运用具体活动的场景或提供学习资源以激起学习者主动学习兴趣、提高学习效率的一种教学方法[1].约翰·杜威(John Dewey)曾指出“思维源于直接经验的情境”[2].

“问渠哪得清如许，为有源头活水来.”生活是知识的源泉，教师在讲授每个知识点时，尽量寻找贴近生活的实际问题作为切入点，从生活实例出发，创设情境，使学生意识到学而有用，促使学生在生活中体验，在体验中感悟，在感悟中成长，在成长中双赢.

例1“二项式定理”第一课时教学片段(多媒体展示)

本节课是学生学习的难点，若学生认为学而无用，则学生就会在上课时学习无兴趣，精力不集中，态度不端正.为了挽救学生“人在曹营心在汉”的不利困境，教者借助学生非常关心的沙漠化问题精心设计了此节课的开头及结尾，既激发了学生求知欲望，又有利于学生挖掘其中人文关怀的内涵.

教师：请问大家从右边图片中看到什么景色？

学生：一望无际的沙漠与几颗枯萎的小草.(有些学生大声地回答道，但不知道老师葫芦里卖的什么药)

教师：我国沙漠化现象日益严重，若不采取有效措施，就会逐渐导致水源枯竭、草场退化，甚至草场毁灭.现在来看一道有关沙漠化的问题.

我国最严重的沙漠化发生在东起吉林省白城——西至宁夏盐池的农牧交错地区，已知该地区已经沦为沙漠化的面积约为5.9万平方千米，若再不采取措施，科学家估计以后每年会以5%的速度向周边地区扩展，那么10年之后该地区的沙漠化面积大概是多少万平方千米？(精确到0.1万平方千米)

通过师生分析、探讨与归纳，学生很快得到10年之后该地区的沙漠化面积大概为5.9×(1+5%)10万平方千米.

教师：怎么计算(1+5%)10的近似值呢？(激发学生思考，引出课题)

设计意图：通过关注民生的情境教学，激发学生学习、探究的兴趣，使原本枯燥无味的课堂变得生动有趣，让学生在贴近生活的实际问题中探索新知识，发现新知识，理解新知识；体验探索的快感，发现的乐趣，收获的喜悦.

二、大刀阔斧，探究新知

如果拘泥于教材，提示学生从n=2，3特殊情况入手，放手让学生去探究，学生能探究出展开式的项数、字母排列的规律，但学生很难归纳出项的系数的规律.就是学生事先预习过了，也很难认识各项系数的本质.项的系数的规律无疑是本节课探究的难点.为了突破此难点，我采用了“低起点，巧迁移，多活动，再升华”的逐级探究方法.

(一)低起点，寻求问题

先探求二项式定理(a+b)n的特殊情况n=2，3，并寻找展开式项数、字母排列和系数的规律.

学生很容易总结出如下规律：(1)当n每增加1时，项数就增加1项；(2)其中一个字母按降幂排列，另一个字母按升幂排列，且每项的次数和都相等.系数的规律是很难的，可能有的学生找的是首末两项系数为1，中间项系数都等于n，但当n=4时就不适合了.一般不会想到把系数与组合数联系起来，这是本次探究的难点.

设计意图：在学生已有的知识结构体系下，培养学生观察、猜想与验证能力.

(二)巧迁移，化解难点

考虑到学生已经具备了一定的排列组合知识，为了化解难点，故把各项系数问题设计成学生耳熟能详的摸球方法数探究问题.

每个括号里有两个字母a和b，相当于每个容器中放标有“a”“b”的球各一个；从3括号中各取一个字母组成某项，等价于从3个容器中各取一球.通过教师的巧妙迁移，学生很快达成共识.

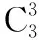
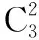
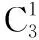
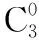
设计意图：陌生问题迁移化，帮助学生搭建一个缓冲的台阶，让学生体会到学会搭建台阶的重要性.

(三)多活动，再试牛刀

百尺竿头，更进一步.鼓励学生运用刚才的迁移方法，把(a+b)4，(a+b)5，……分别展开.这个工作非常重要，因为学生通过取得阶段性的成果，学生会深深体会到解决了一个光靠多项式乘法来展开二项式的局限性的喜悦感与成就感，把系数问题巧妙地转化为组合数概念的魅力与威力.

设计意图：给学生搭个台阶架子，让学生自己铺上板成为台阶，呈现“一路楼台直到山顶”的意境.

(四)再升华，修成正果

有了前面三步作为铺垫，学生很自然地归纳并推导出了二项式定理的一般形式，知道n=2，3是二项式定理的特例，二项式定理是它们的推广.紧接着引导学生学习二项展开式的通项、二项式系数等.

设计意图：通过学生间合作交流与探究，教师点拨提示，学生亲身经历了知识的发生、发展和形成过程，在探索、发现、归纳，再探索、再发现、再归纳中对二项式定理的相关知识形成自然生成、自然记忆和自然理解.更重要的是学生的迁移能力得以锻炼，得以优化，得以提升.

有些教师在教学时直接给出(a+b)3的展开形式，觉得简单，没必要花时间探究项的系数形成的原因.但笔者认为正是因为它发生在学生的已有认知范围内，才能诠释“麻雀虽小，肝胆俱全”这样的深刻道理，才有利于培养学生由浅入深，由简单到复杂，由特殊到一般，由具体到抽象的逻辑思维能力、技能迁移能力.

三、乘胜追击，强化新知

数学家哈尔莫斯说：“有了问题，思维才有了方向.”作为教学的主导者，教师要灵活运用一题多问、一题多变等“六题艺术”，把例题作适当延伸，增加习题的难度、宽度与新颖度，给学生提供自主探究、合作探究、逐层探究问题的契机以及分析问题、解决问题的平台.(例题较简单，解题过程略)

例1用二项式定理展开下列各式，并求二项展开式的通项：

(1)(2x+y)6；(2)(x+2y)6.

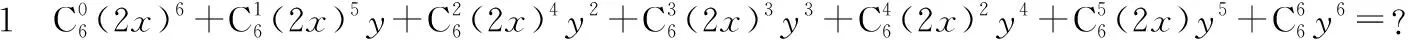
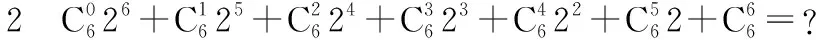
设计意图：通过例1中解题过程进行比较，加深探究二项展开式的通项中的字母顺序、指数、形式等特点.例1及其变题能使学生深刻地认识到二项式定理是恒等式，即能正向运用，也能逆向运用，当然也能赋值.

例2求(1+2x)7的展开式中第4项的二项式系数和系数.

变题1求(1+2x)7的展开式中倒数第5项的二项式系数和系数.

变题2若(1+ax)7的展开式中x3的系数为280，求实数的值a.

变题3求(1+2x)7的展开式中中间两项的二项式系数和系数，并观察它们之间关系.

设计意图：巩固二项展开式的通项的运用，探究二项式系数和系数的特点与联系，并为学生下一节课的学习埋下伏笔.

例3情境回归：若不采取措施，10年之后该地区的沙漠化面积大概是多少万平方千米？(精确到0.1万平方千米)

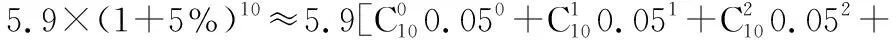
啊！10年之后该地区的沙漠化面积约占我国总面积的百分之一！学生不由自主地触目兴叹，且很自然地意识到有些灾害既有客观因素也有主观因素.有时人类为了追求高利润、高回报，人为地造成植被破坏、水土流失、荒漠蔓延、酸雨肆虐、洪水泛滥、天气干旱、资源匮乏、物种消失等一系列后果人类不能及时反省，则人类的生存状况就会每况愈下.

设计意图：通过实际问题的解决，让学生体会到数学是生动的，数学是源于生活的，高于生活的，服务于生活的.求近似值是二项式定理在实际生活中的一个重要应用，先把展开后的项按精确度保留，再求这些项的和即可.通过情境问题的解决，使得本节课首尾呼应巧收笔、相得益彰，此种独具匠心的设计把学生的学以致用的热情推向高潮.(限于篇幅，其余环节不再赘述)

四、对探究问题设计的几点思考

(一)探究问题的设计要尊重学生的个体差异

教师在设计问题时，要根据学生的个性差异将学生分成多个层次，然后，在各个层次中根据学生的认知水平设计出相应的问题，较难的问题让基础较好的学生解答，较易的问题让学困生回答.在学生阐述完观点后，教师要及时引导学生进行研讨、总结、归纳、论证、弄清重点、突破难点，消除学生在知识上的疑惑点和疑难点，以便让学困生也思有所益、学有斩获.

(二)探究问题的设计要有梯度

探究问题的难易程度大小，要根据学生个性的特点及学生的即时表现等来决定是否“搭台阶”“搭多高台阶”以及“由谁搭台阶”.若需“搭台阶”时要将问题有机地、合理地、科学地分成若干个子问题，使各个子问题都在教学目标之内，易落实、能实现.

(三)探究问题的设计要有连续性

问题的设计要具有连续性是指灵活运用多种教法和学法对一个问题进行多角度、多层次、全方位的挖掘与探讨，或运用形同质同、形同质异、形异质同、形异质异等技巧对问题进行科学的“整容”，灵活更换题目的条件或结论，尽量保持处理问题的技巧、技能不变，解题的思想方法不变.

(四)探究问题的设计要有启发性[3]

启发性是问题的设计灵魂，教师要注重运用教材知识点和经验之间的矛盾当作问题设计的突破口，常设计一些多思维指向、多思维途径、多思维结果的问题，保持问题不落俗套，具有新鲜感，刺激学生主动地去发现、去探索.

(五)教师要把握好探究的角色

教师的探究的角色定位要恰当.探究是学生展示才能和智慧的舞台，作为教学的主导者一定不要“越俎代庖”，力争做到“发于该发，止于该止”.在每个探究问题中都扮演着“俊也不争春，只把春来报，等待山花烂漫时，她在丛中笑”的角色，要集中于数学生成，培养学生的自主思考与探讨能力.

德国数学教育理论专家栋科教授认为：“思维着的教学活动，决定着教学的质量”.因此，为使数学教学有效，就必须让学生多观察、多动手、多思考、多探究，只有每一个环节都充满着思维的有效探究活动，数学教学才会更有效.