浅谈初中数学中的最值问题

◎侯丽娜　刘　君

(1.吉林省公主岭市桑树台镇中学，吉林　公主岭　136100；2.北华大学数学与统计学院，吉林　吉林　132000)

最值问题是初中数学中常考的一类问题，解决此类问题，要求学生掌握数学分支知识，能够综合运用各类数学技巧，灵活选择合理的解题方法，还考查学生的运算能力、分析问题和解决问题的能力.初中数学中常考的最值问题大致分为如下几种.

一、利用“垂线段最短”求最值

例1点A的坐标为(-1，0)，点B的坐标为(a，a)，当线段AB最短时，求点B的坐标.

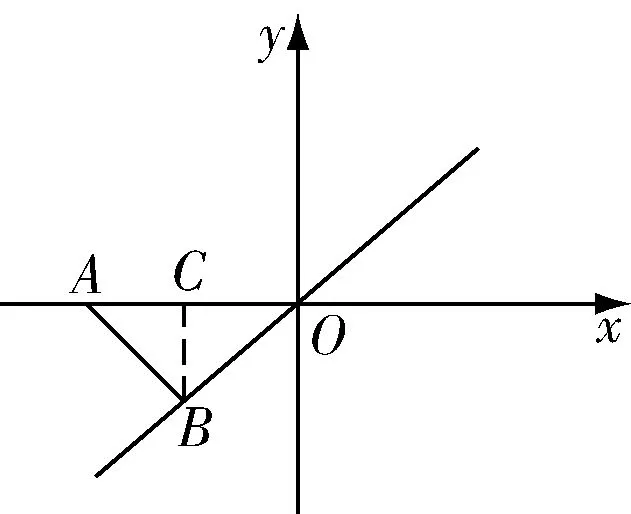
图1

本题主要考查点到直线的距离，如图1所示，根据“点到直线的距离，垂线段最短”可得，当AB垂直于直线y=x时，线段AB最短.根据OA距离、直线解析式以及∠AOB的度数可得出△OAB为等腰直角三角形，点B为顶点，根据三角函数关系得出OC、CB的长度，由于点B在第三象限，因而，可得出点B的坐标.

二、利用“轴对称”求最值

图2

例2如图2所示，菱形ABCD的边长为4，∠BAD=120°，点E是AB的中点，点F是AC上的一动点，求EF+BF的最小值.

本题主要考查菱形和图形的轴对称，根据题意做出辅助线可知，ED的长即为EF+BF的最小值，根据角度以及边的数量关系求出其他边长，根据勾股定理得出最小值.

解决一个动点到两个定点的距离之和的最小值问题，可以利用“轴对称”的知识将其中一条线段转化为与其相等的另一条线段，然后利用“两点之间线段最短”求出距离之和的最小值.

三、利用“三角形三边关系”求最值

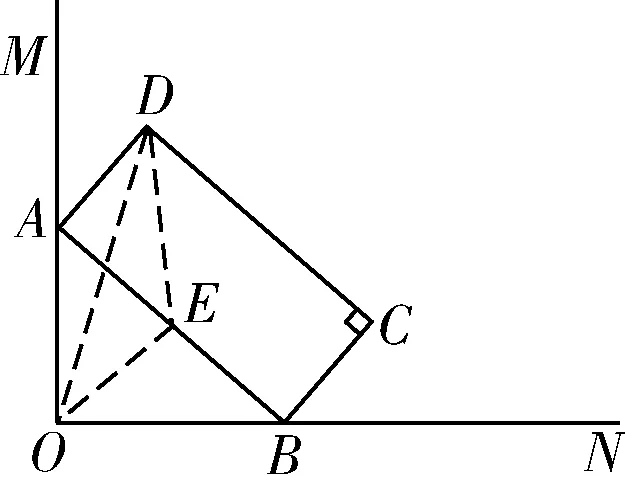
图3

例3如图3所示，∠MON=90°，矩形ABCD的顶点A，B分别在边OM，ON上，当B在边ON上运动时，A随之在边OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离是多少？

本题考查了直角三角形斜边上的中线等于斜边的一半的性质，三角形的三边关系，矩形的性质和勾股定理.根据三角形的任意的两边之和大于第三边可知，取AB的中点E，连接OE，DE，OD.则OD小于等于OE+DE，当O，D，E三点共线时，点D到点O的距离是解题的关键.

四、函数中的最值

函数中的最值问题通常是利用函数知识来解决实际问题，根据题意在实际问题中建立函数关系，再利用函数性质来解决其中的问题，有时需要与其他相关知识相结合.这部分内容是中考中的重点与热点，体现了数学的应用价值.

例4服装店准备购进甲、乙两种服装，甲服装每件进价80元，售价120元；乙种服装每件进价60元，售价90元，计划购进两件服装共100件，其中甲服装不少于65件，不多于75件，该服装店对甲服装以每件优惠a(0

本题综合运用函数以及不等式(组)来解决实际问题，根据题意可得利润W=(40-a)x+30(100-x)=(10-a)x+3 000，根据a的不同范围来确定在x取值不同的影响下W的最值情况.本题中要注意一次函数y=kx+b，当k>0时，函数值y随x的增大而增大：当k<0时，函数值y随x的增大而减小.

解决函数中最值问题的基本方法：

(1)根据题意建立函数关系式；

(2)根据实际意义建立关于自变量的不等式(组)；

(3)根据函数自变量的取值范围，确定符合条件的方案；

(4)利用函数的性质求最大值或最小值.

在代数里最值问题多出现在函数部分，无论是一次函数、反比例函数、二次函数，一般是先求自变量的取值范围，再求解析式，根据实际问题求出最值.在几何中的最值问题是指当某几何元素在给定条件变动时，求某几何量(如，线段的长度、图形的面积、角的度数)的最大值或最小值问题.几何最值问题常以动点、轴对称、旋转为背景，解题时需要运用动态思维、数形结合、特殊与一般相结合、逻辑推理与想象相结合等多种思想方法.在初中数学的学习中灵活运用所学的思想方法，提高学习效率，提升学生整体水平.