数学问题解答

2018年2月号问题解答

(解答由问题提供人给出)

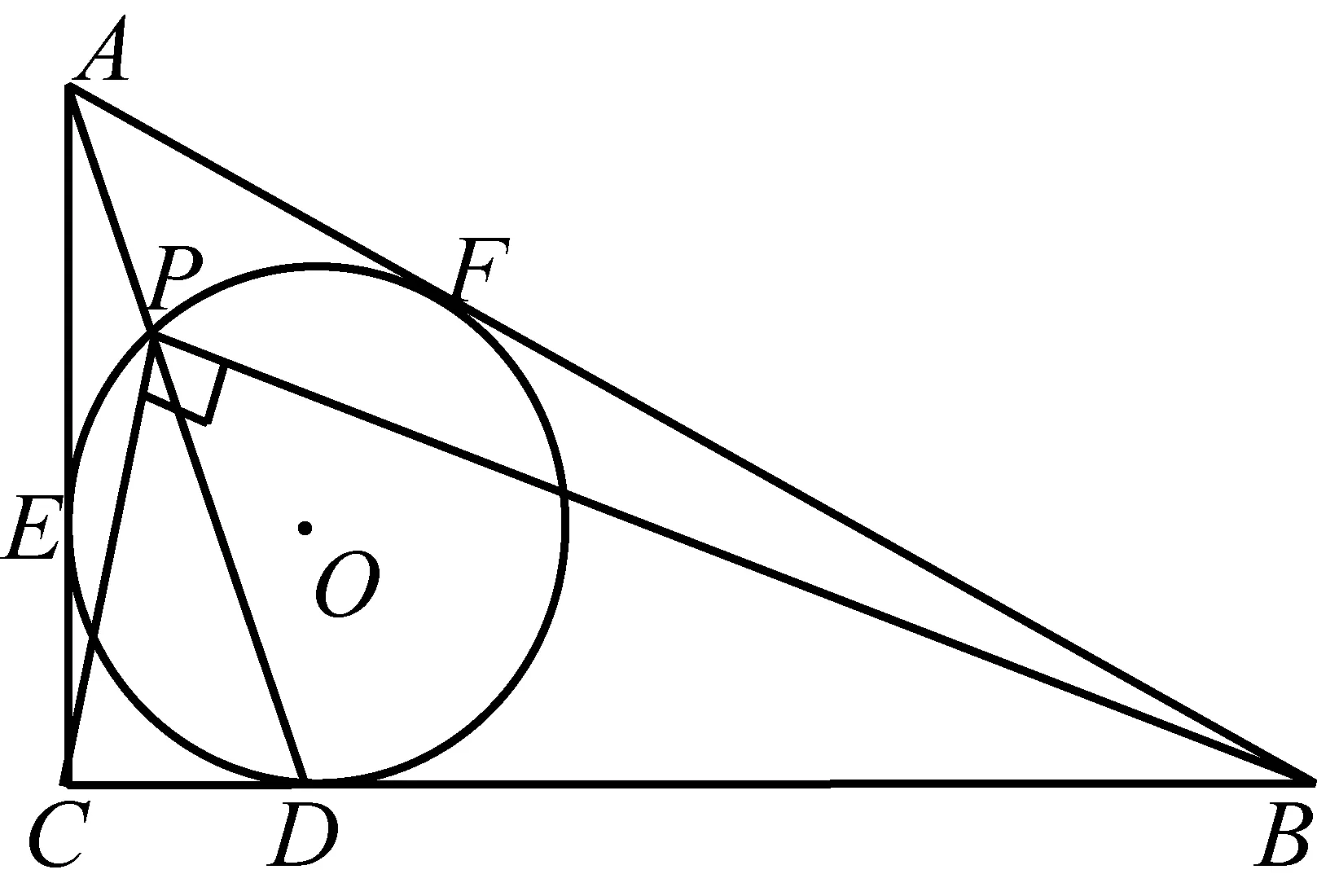
2406在直角三角形△ABC中，∠ACB=90°，△ABC的内切圆O分别与边BC,CA,AB相切于D,E,F，连接AD与内切圆O相交于点P，连接BP,CP.若∠BPC=90°，求证：

AE+AP=PD.

(山东省滕州市第一中学 颜子皓 277500)

证明设AP=1,BD=BF=x,

CE=CD=y,AE=AF=m(m>1)，

AF2=AP·AD⟹AD=m2,

PD=AD-AP=m2-1，

BP2=12+(m+x)2-2(m+x)·1·cos ∠BAD，

因为CP2+BP2=(y+x)2，

=y2+x2+2xy，

所以(m2-1)(x+y)=mxy

①

又cos ∠ADC+cos ∠ADB

由①②得m4-m2=4(m2-1)，

即m4-5m2+4=0,即(m2-4)(m2-1)=0，

又m>1,所以m2=4,m=2，

所以AD=4,AE=2，

得PD=4-1=3，

所以PD=AE+AP.

(浙江省温州市洞头区第二中学 陈展 325701)

证明记原不等式为 (1)

其中分母恒大于0.

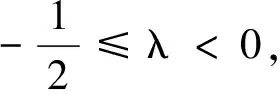
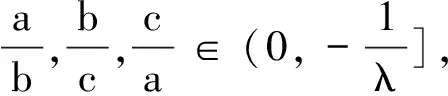
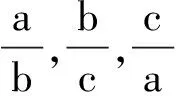
⟺(λ+2)a3>(1-λ)a3+(1-λ)λa2b+(1-λ)ab2

⟺(2λ+1)a3+(λ-1)λa2b+(λ-1)ab2>0

⟺(2λ+1)a2+(λ-1)λab+(λ-1)b2>0

⟸(λ-1)λa2b+(λ-1)ab2>0

⟺(λ-1)λa2b>(1-λ)ab2

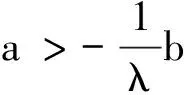
⟺λb3+2b3≥b3+λb2c+bc2

⟺(λ+1)b3-λb2c-bc2≥0

⟺b[(λ+1)b+c](b-c)≥0也显然成立.

所以(1)式成立.

所以(1)式也成立.

综上可知(1)式成立.

2408如图，AC是⊙O的直径，BD是⊙O的弦，AC⊥BD，垂足为E．F在DA的延长线上，G在BA的延长线上，且BF∥DG，GF的延长线与DB的延长线相交于I．H在线段IF上，且H、B、E、F四点共圆，IC的延长线与GD的延长线相交于K．求证：IK⊥GK．

(河南省南阳市宛城区新店二中向中军473113)

证明连结BC、BH、CG、CH、EH、EF.

AC是直径，AC⊥BD，

所以AB=AD，∠ABC=∠BEC=90°，

有AB2=AE·AC.

由BF∥DG，有 △ABF∽△AGD，

又 ∠BAE=∠DAE，∠BAF=∠GAD，

故∠EAF=∠GAC，

所以 △AEF∽△AGC，

故∠AEF=∠AGC，∠FEB=∠BCG.

由H、B、E、F四点共圆，

有 ∠FEB=∠IHB，故∠BCG=∠IHB，

所以H、B、C、G四点共圆，

所以∠GHC=∠ABC=90°，

∠IHC=90°=∠BEC，

故H、I、C、E四点共圆，

故∠ICH=∠IEH=∠IFB.

由BF∥DG，有∠IFB=∠IGD，

故∠IGD=∠ICH，

故G、H、C、K四点共圆，

故∠K+∠GHC=180°，

故∠K=90°，IK⊥GK．

2409设△ABC中的三边长分别为a,b,c，外接圆和内切圆半径分别为R,r，求证：

(1)

(河南质量工程职业学院李永利467000)

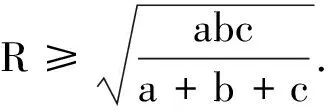
(2)

故(2)式成立．

2.其次证明

(3)

⟺(ab+bc+ca)2≥3abc(a+b+c)

(注：ab+bc+ca=p2+4Rr+r2，abc=4Rrp，a+b+c=2p)

⟺(p2+4Rr+r2)2≥24Rrp2

⟺p4+2(4Rr+r2)p2+(4Rr+r2)2≥24Rrp2

⟺p2·p2+(4Rr+r2)2≥(16Rr-2r2)p2.

由Gerretsen不等式p2≥16Rr-5r2可知，只需证

(16Rr-5r2)p2+(4Rr+r2)2

≥(16Rr-2r2)p2

⟺(4Rr+r2)2≥3r2p2

⟺(4R+r)2≥3p2.

由上式和Gerretsen不等式p2≤4R2+4Rr+3r2可知，只需证明

(4R+r)2≥3(4R2+4Rr+3r2)

⟺4R2-4Rr-8r2≥0

⟺R2-Rr-2r2≥0

⟺(R+r)(R-2r)≥0.

而由Euler不等式R≥2r可知上式显然成立，从而(3)式成立．

3.最后证明

(4)

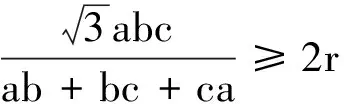
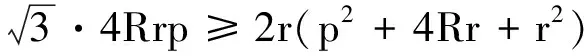
⟺12R2p2≥(p2+4Rr+r2)2

⟺12R2p2≥p2·p2+(8Rr+2r2)p2+(4Rr+r2)2.

由上式和Gerretsen不等式p2≤4R2+4Rr+3r2可知，只需证明

12R2p2≥(4R2+4Rr+3r2)p2+(8Rr+2r2)p2+(4Rr+r2)2

⟺(8R2-12Rr-5r2)p2≥(4Rr+r2)2.

由上式和Gerretsen不等式p2≥16Rr-5r2可知，只需证明

⟺(8R2-12Rr-5r2)(16Rr-5r2)

≥(4Rr+r2)2

⟺(8R2-12Rr-5r2)(16R-5r)

≥r(4R+r)2

⟺128R3-232R2r-20Rr2+25r3

≥16R2r+8Rr2+r3

⟺128R3-248R2r-28Rr2+24r3≥0

⟺32R3-62R2r-7Rr2+6r3≥0

⟺(32R2+2Rr-3r2)(R-2r)≥0.

而由Euler不等式R≥2r可知上式成立，从而(4)式成立．

由(2)，(3)，(4)式可知(1)式成立．

2410如图，O为△ABC内一点，角A,B,C所对的边为a,b,c，延长AO,BO,CO交△ABC的三边和外接圆分别为D,E,F,A1,B1,C1，求证：

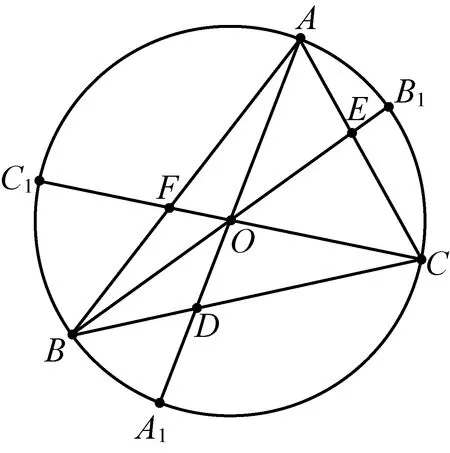
(安徽省安庆市岳西县汤池中学 苏岳祥 杨续亮246620)

在△A1DC中，由正弦定理可得

而∠DCA1=∠DAB=∠DAC-α=A-α，

∠BA1C=∠ABC=B，

由正余弦定理可得

以上三式相加可得

2018年3月号问题

(来稿请注明出处——编者)

2411设x,y为正整数,x2+y2-2017xy>0且不是完全平方数,求x2+y2-2017xy的最小值.

(四川省成都七中 方廷刚 610041)

2412在锐角△ABC中，O为外心，H为垂心，I

( 安徽省安庆市岳西县汤池中学杨续亮246620)

2413设AB和CD为圆O的两弦，AB的延长线与CD的延长线交于点E，AD与CB交于点F，以EF为直径的圆O′与圆O交于点P和Q，证明：圆O和圆O′在交点P或Q处的切线互相垂直.

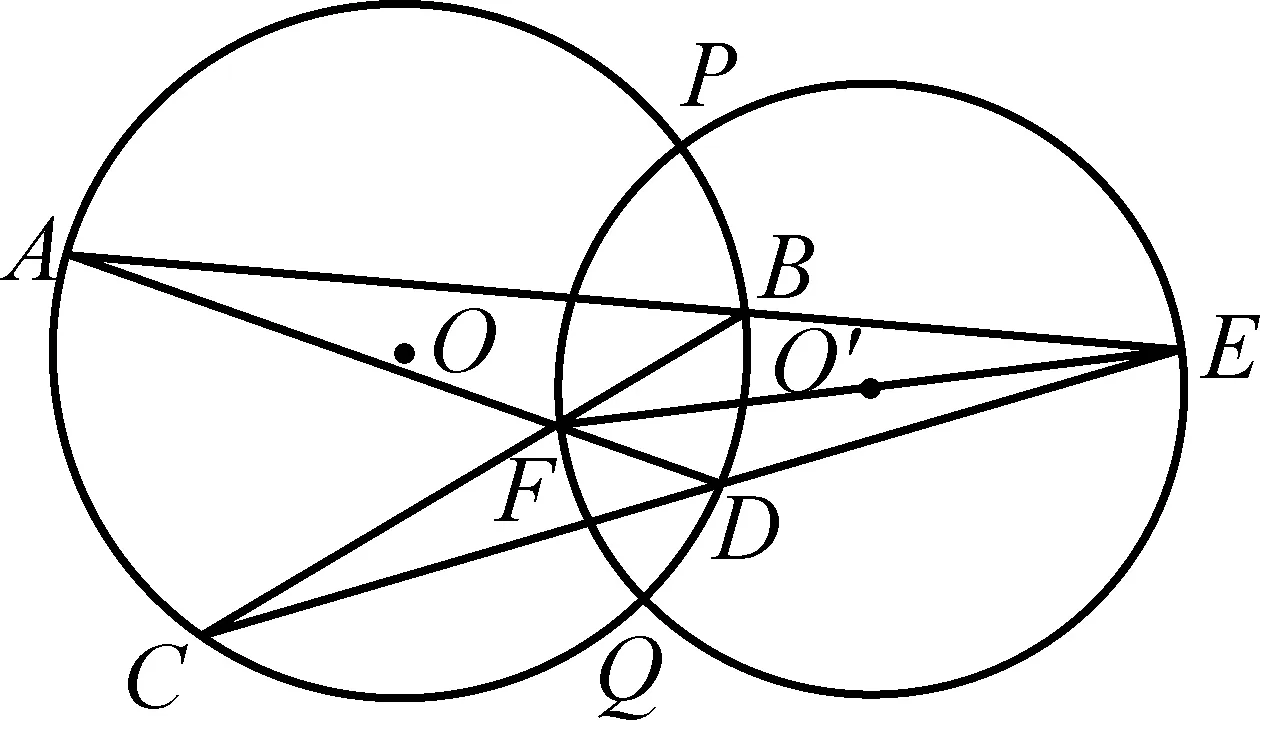
(河南省辉县市一中贺基军453600)

2414已知a,b,c>0,a+b+c=3,求证：

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000)

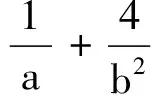
(四川省西充中学李光俊637200)