变式不任性 教学价更高*

张　俊

(江苏省兴化市第一中学　225700)

变式教学是我国数学教学传统中的重要内容，植根于本土，又得到现代教育理论的哺育．有效利用变式教学，不仅可以扩大教学容量，节约课堂时间，还可以增加课堂情趣，为教师的教学添彩增色．

在听课过程中，笔者发现，由于对变式教学的本质理解不到位，教学中出现了一些异化现象，如：不考虑知识的逻辑顺序，忽视学生已有的认知水平，为变式而变式；变式数量过多，片面追求面面俱到，造成新的题海；变式难度盲目拔高，增加学生接受负担，造成新的无意义学习；变式不问质量，生搬硬拉，干扰了学生对主干知识的理解；变式不考虑时机，游离于教学目标之外，无视学生负面情绪的积累；不考虑师生双边的互动，自己一变到底，一讲到底，造成新的教师一言堂．

针对变式教学中出现的不合理现象，笔者提几点建议，供大家参考．

1　变式要有导向性

对于同一则材料，可以从不同的角度进行不同形式的变式．不同的变式，有着不同的作用．做出每一个变式，教师心中都要有数：你提供这个变式的目的是什么？你想达到什么目标？你想让学生做到什么，获得什么？在变式前，教师必须要反复权衡，慎重考虑．

案例1在三棱锥A-BCD中，点E,F,G,H分别是边AB,BC,CD,DA的中点，求证：四边形EFGH是平行四边形．

此题为苏教版必修2中的一道习题．针对不同的教学目的，可给出不同的变式．

如果想培养学生处理探索性问题的能力，改变此题的设问方式，得到：

变式1： 在三棱锥A-BCD中，点E,F,G,H分别是边AB,BC,CD,DA的中点，试判断四边形EFGH的形状．

如果想培养学生逆向思考问题的意识，可考虑提供如下变式：

变式2：在三棱锥A-BCD中，点E,F,G,H分别是边AB,BC,CD,DA的点，若四边形EFGH是平行四边形，E,F,G,H一定要是各边的中点吗？

如果想潜移默化的培养学生合情联想的习惯，深化问题的意识，提出问题的能力，可提出如下变式：

变式3： 在三棱锥A-BCD中，点E,F,G,H分别是边AB,BC,CD,DA的中点，问：当AC,BD满足什么条件时，四边形EFGH是菱形？你还能提出什么样的问题？

如果想培养学生的开放性思维水平，可考虑提供如下变式：

变式4： 在三棱锥A-BCD中，点E,F,G,H分别是边AB,BC,CD,DA上的点，若四边形EFGH是平行四边形，还需添加什么样的条件？

如果学生学习基础较好，学习欲望强，还可给出：

变式5： 在三棱锥A-BCD中，点E,F,G,H分别是边AB,BC,CD,DA的中点，若AC=BD=2，试求EG2+FH2的值．

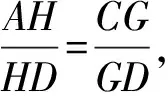
教师在变式之前必须深思熟虑，结合课标、教学内容、学生知识水平、能力现状等进行综合考虑，到底是为了使学生理解某一概念，揭示某一规律，还是使学生掌握某一方法，领悟某种思想，一定要根据不同的教学实际和需要去做出决定．

2　引入变式要适时

作为对授课内容的有益助手，变式教学需要把握好引入变式的时机．只有在恰当的时候引入恰当的变式，教学和训练才能达到预期的效果，否则，哪怕所提供的变式再精彩，再漂亮，也毫无价值，起不到应有的作用．引入每一个变式，教师都要思索什么时候引入的时机最佳，效果最好．

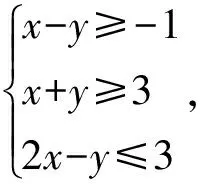
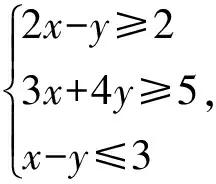
该变式试图通过改变平面区域来改变最终的结论，但忽视了平面区域为上节课所学重点，因而此变式虽然能达到对旧知识的巩固，却耽搁了学生思考问题获取新知的时间．

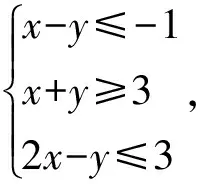
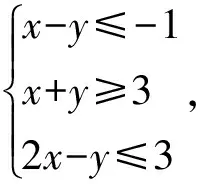
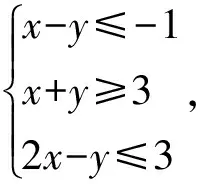
相对于原题，变式1将可行域由封闭变为开放，变式2中的目标函数z=2x+y所表示的动直线的斜率发生了变化，变式3不仅目标函数所表示的动直线的斜率发生了变化，最优解的个数也发生了变化．这三个变式既考虑到了本节课的目标，也注意到了学生的认知水平，不仅具有明确的导向性，也符合适时性，让学生不需花过多时间就能深刻理解目标函数与可行域之间的联系，获得理性的认识．以上变式通过一道题目的变化就让学生掌握了线性规划图解法所涉及的各种情形，经济实效．

3　变式要有层次性

变式的层次性是指变式时要循序渐进，梯度分明，层次清晰，跨度合理．变式之间的跨度过大，会使学生产生畏难心理，妨碍学生的接受理解和问题的解决；跨度过密，则失去思考价值，也并不利于学生的思维发展．

当然，层次的疏与密与学生的学习水平密切相关，也许对于基础薄弱的学生跨度大的变式，对学优生则不成问题．总之，要体现有效变式的层次性需要教师认真研究学情，准确把握学生学习的潜在距离，从学生的认知水平出发，将变式设计在学生的最近发展区内．

对于一些较难的概念或问题，教师可尝试设计一些低起点的变式以分解难度，促成学生的有效学习；而对于一些表面平凡却内涵丰富的问题，教师不能轻易放弃其中蕴藏的教学价值，要尝试以此为生长点，带领学生“引题深入”，通过一系列层次合理的变式问题培养学生的多方面能力．

案例3已知函数y=log2(ax2+2x+3)的值域为R，试求实数a的取值范围．

这是历届学生都普遍感到困难，不易理解的问题，笔者在教学实践中借助富有梯度，层次适当的的变式问题串，有效的突破了这一难点，学生普遍反应良好．

变式1： 求函数y=log2x(x>0)的值域．

变式2： 求函数y=log2(x2+1)的值域．

变式3： 求函数y=log2(x2-1)的值域．

这三个变式的解决使学生从源头上理解了函数y=log2(ax2+2x+3)的值域为R的原因，为问题的解决立下汗马功劳．在此基础上，再引入如下变式：

变式4： 已知函数y=log2(ax2+2x+3)的值域为[2,+∞)，你能得到什么？

通过变式4，使学生深入理解了y=log2(ax2+bx+c)型函数值域的本质，学生的理解难点瞬间消解，思维通道畅通无碍，实现了问题的解决．

根据学生情况和教学要求，可酌情考虑是否给出如下形似质异的变式题：

变式5：已知函数y=log2(ax2+2x+3)的定义域为R，试求实数a的取值范围．

变式5与原题外形相似，本质相异，通过这两道题促使学生在比较中认真推敲它们之间的联系与区别，从而对问题的理解更透彻、更清晰，使学生的思维再达一个新的层次．

4　变式要注意学生的参与度

教学中引入变式的目的是希望以较少的教学投入获得最大的教学效益，最终是为了促成学生的发展．教师要时刻做到：眼中有学生，心中有学生，一切为了学生．既然如此，变式教学中必须要考虑学生的可参与性．没有学生主动参与的变式是不合格的变式，没有学生投入情感的变式是无用的变式．只有学生积极主动的参与，才会有变式教学的最佳收益，才能取得理想的教学效果.

案例4求函数y=x+1，(x∈[-1,2])的值域．

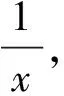
学生受此启发，会打开思路，提出种种类似问题，如：

变式2：求函数y=x2+1，(x∈[-1,2])的值域．

变式4： 求函数y=2x+1，(x∈[-1,2])的值域．

类似的还会有很多，学生提出的问题不一定都能解决，这就需要教师合理掌控，准确点评，要注意不能轻易否定学生，表扬与鼓励齐飞，激励共建议同行．

为了帮助学生学会提出问题，教师可以适时再次示范：如从逆向角度我们还能提出什么问题呢？比如：

变式5： 如果函数y=kx+b，(x∈[-1,2])的值域为[0,2]，试确定实数k,b的值．

在教师的启发，引导下，学生会主动提出各种各样的变式，如：

变式6： 如果函数y=ax2+x+b，(x∈[-1,2])的值域为[0,2]，试确定实数a,b的值．

变式7：如果函数y=asinx+b的值域为[0,2]，试确定实数a,b的值．

变式8： 如果函数y=log2(kx+b)的定义域和值域都是[0,2]，试确定实数a,b的值．

教师可以进一步的启发，以激发学生主动参与的欲望：你能将原问题与数列知识结合起来吗？向量呢？……

通过亲身参与变式，学生会感觉到数学学习的无穷乐趣，感觉到出题并不神秘，感觉到数学习题冰冷的外表下隐藏着亲切可爱，在润物细无声中，提高了学生的数学思维水平，培养了学生的数学探索能力．

变式教学是被广大数学教师自觉或不自觉使用的教学策略，惟其如此，我们更需要合理地运用这一策略，每一个变式都不能不能兴之所行，任意发挥，而要反复斟酌，通盘考虑，这样才能真正的发挥变式教学的作用，以提高教学效益，促进学生成长．