三个三角形不等式的指数推广链及其类似
2018-07-14黄兆麟
黄兆麟
(天津水运高级技工学校 300456)
在△ABC中,设∠A,∠B,∠C的对边分别为a,b,c,则有
(1′)
(2′)
(3′)
本刊文[1]给出了以上三个三角形不等式不同风格的证明,但不宜指数推广,本文则给出这三个不等式指数推广的证明,方法异于文[1].首先将不等式(1′)及(2′)统一推广为:
定理1在△ABC中,设∠A,∠B,∠C的对边分别为a,b,c,则当指数k≥1,有
≥akcosA+bkcosB+ckcosC
(Ⅰ)
证明首先分两部分证明不等式链(Ⅰ)中第一个不等式.
①当k=1时,不等式链(Ⅰ)中第一个不等式即为不等式(2′),而由正弦定理知不等式(2′)又可等价为如下不等式(1),
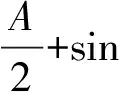
(1)

设此时不等式(1)左右之差为M1,则
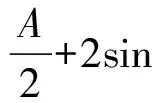
-sin (B+C)-sin (C+A)-sin (A+B)
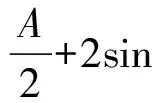
-(sinBcosC+cosBsinC)-(sinCcosA
+cosCsinA)-(sinAcosB+cosAsinB)
显然以上最后一式的三个单项均为非负项,故有2M1≥0,即不等式(1)成立,
从而不等式(2′)成立,也就是当k=1时不等式链(Ⅰ)中第一个不等式成立.
②当k>1时,由不等式链(Ⅰ)中第一个不等式的完全对称性,不妨设A≥B≥C,则有
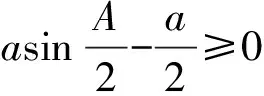
又记此时不等式链(Ⅰ)中第一个不等式左右之差为M,那么

即当k>1时不等式链(Ⅰ)中第一个不等式也成立.
以上证明最后一步用到了不等式(2′)成立的结论.
综上①与②知当k≥1时不等式链(Ⅰ)中第一个不等式成立.
由以上证明过程可看出,不等式(2′)强于不等式(1′).
下面再证明不等式链(Ⅰ)中第二个不等式:
由不等式链(Ⅰ)中第二个不等式的完全对称性,不妨设A≥B≥C,则有
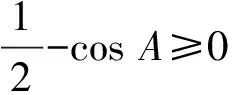
又记此时不等式链(Ⅰ)中第二个不等式左右之差为M2,那么

即当指数k≥1时不等式链(Ⅰ)中第二个不等式也成立.
以上证明最后一步用到了熟知的不等式
至此定理1全部获证.
顺便指出,由以上证明过程不难看出,对于不等式链(Ⅰ)中的第二个不等式,指数可放宽为正数.
下面再将不等式(3′)指数推广为:
定理2在△ABC中,设∠A,∠B,∠C的对边分别为a,b,c,且指数k为正数,则有
(Ⅱ)
证明首先给出不等式链(Ⅱ)中第一个不等式一种直接证法(下文还有一种间接证法).
由不等式链(Ⅱ)中第一个不等式的完全对称性,不妨设A≥B≥C,则有

又记此时不等式链(Ⅱ)中第一个不等式左右之差为M,那么
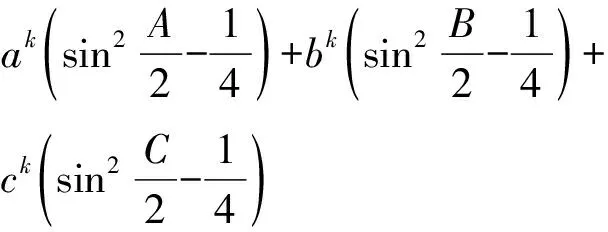
即不等式链(Ⅱ)中第一个不等式成立.
以上最后一步用到了熟知的不等式
下面再证明不等式链(Ⅱ)中第二个不等式:
将不等式链(Ⅱ)中第一个不等式里的正弦函数,利用平方关系置换为余弦函数即得
即不等式链(Ⅱ)中第二个不等式也成立.
至此定理2全部获证.

接下来再给出定理1的一个类似.
定理3在△ABC中,设∠A,∠B,∠C的对边分别为a,b,c,则当指数k≥1,有
(Ⅲ)
证明首先分两部分证明不等式链(Ⅲ)中的第一个不等式
①当k=1时,设此时链(Ⅲ)中第一个不等式左右之差为M11,利用余弦定理可得
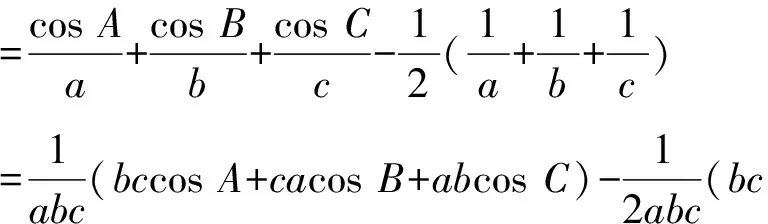
+ca+ab)
即当k=1时链(Ⅲ)中第一个不等式成立.
②当k>1时,由不等式链(Ⅲ)中第一个不等式的完全对称性,不妨设A≥B≥C,则有

又记此时不等式链(Ⅲ)中第一个不等式左右之差为M12,那么

即当k>1时不等式链(Ⅲ)中第一个不等式也成立.
以上证明最后一步用到了k=1时链(Ⅲ)中第一个不等式成立的结论.
综上①与②知当k≥1时不等式链(Ⅲ)中第一个不等式成立.
下面再证明不等式链(Ⅲ)中第二个不等式:
由不等式链(Ⅲ)中第二个不等式的完全对称性,不妨设A≥B≥C,则有
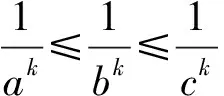
又记此时不等式链(Ⅲ)中第二个不等式左右之差为M2,那么
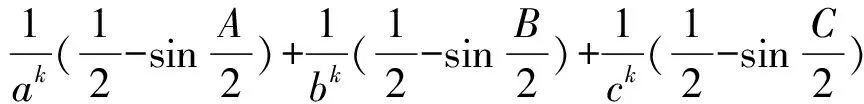
即不等式链(Ⅲ)中第二个不等式也成立.
以上证明最后一步用到了熟知的不等式
至此定理3全部获证.
顺便指出,由以上证明过程不难看出,对于不等式链(Ⅲ)中的第二个不等式,指数可放宽为正数.
下面再给出定理3的一个类似.
定理4在△ABC中,设∠A,∠B,∠C的对边分别为a,b,c,且指数k为正数,则有
(Ⅳ)
证明先证明链(Ⅳ)中第一个不等式.
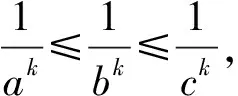
以下证明需分类讨论:

又设链(Ⅳ)中第一个不等式左右之差为M1,那么
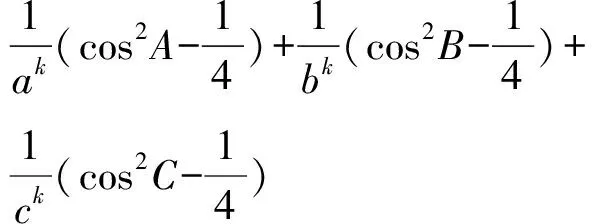
即此时链(Ⅳ)中第一个不等式成立.
以上证明最后一步用到了熟知的不等式

即此时链(Ⅳ)中第一个不等式也成立.
综①和②知链(Ⅳ)中第一个不等式成立.
再证明链(Ⅳ)中第二个不等式也成立:
将不等式链(Ⅳ)中第一个不等式里的余弦函数,利用平方关系置换为正弦函数即得
移项整理即得
即不等式链(Ⅳ)中第二个不等式也成立.
至此定理4全部获证.
