让“数学实验”走进中学课堂
——以对一道全国高中数学联赛试题的再推广为例
2018-07-14孙彦
孙 彦
(安徽省安庆市教育教学研究室 246003)
当前,我国的数学教学改革正在向纵深发展,新的课程标准强调对学生数学核心素养的培养,倡导学习的自主性、探究性.然而,在当下的中学数学课堂教学中,为了应对高考,教师在课堂上拼命讲题,学生在课外拼命地刷题,当我们讲了一道道经典的例题时,学生常常会问:“老师,这些结论是怎么得到的?”这不得不引起我们反思,我们的课堂教学,几乎是用一种纯演绎的模式去教会学生如何证明已有的结论,却不能帮助学生去发现未知的结论.
我们知道,数学发现的过程需要借助诸如猜测、归纳之类的思维活动,在猜测、归纳的过程中,往往需要通过大量计算来完成,也正因为如此,传统的课堂教学较难组织“诸如猜测、归纳”之类的思维活动,但在现代,随着信息技术与教学内容的整合,我们可以借助计算机和各种软件,使数学探究也可与自然科学一样,通过“数学实验”让学生去“发现”一个个结论,然后再去证明结论.这样就可以变“被动接受知识”为“主动获取知识”.因此,让“数学实验”走进中学课堂十分必要.
本文利用《几何画板》数学软件,以“数学实验”的手段, 通过对一道全国高中数学联赛试题的实验性探究,让学生去发现问题的本质和更多的结论.
1 问题的提出
在一次高中数学竞赛专题辅导中,笔者首先向学生布置了如下一道题,并提前用《几何画板》数学软件作好该题的实验平台,供学生使用.

(Ⅰ)△PAB的内切圆的圆心在一条定直线上; (Ⅱ)若∠APB=60°,求△PAB的面积.
注:①此题为2011年全国高中数联赛复赛第11题.
②笔者在平时教学中已教会了学生《几何画板》的一些基本使用方法.
2 问题的探究
探究1证明方法的探究
笔者在观察学生做第(Ⅰ)题时,发现有许多学生在尝试求出△PAB的内心坐标,进而求出内心的轨迹,这种想法是合理的,但在实际操作时,由于求内心坐标的过程过于繁杂,学生思维在此受挫.
此时,教师让一位同学在《几何画板》上拖动直线l,观察直线PA、PB斜率的变化,这时学生就会发现“直线PA、PB的斜率始终互为相反数”(如图1所示),发现这一结论后,问题就迎刃而解了.

图1
待学生完成第(Ⅰ)题的证明之后,教师再利用《几何画板》数学软件演示△PAB的内切圆的圆心的轨迹的正确性时,及时向学生提出:“为什么轨迹会是两条折线段呢?”(如图2中粗线部分).
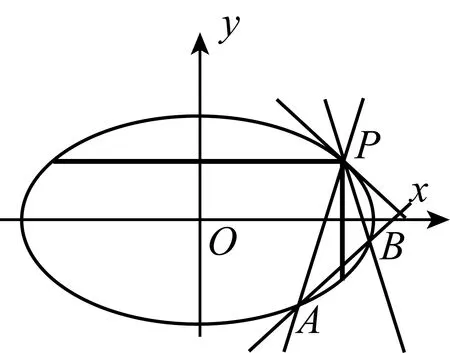
图2
此时在演示的基础上,学生不难得出如下结论:


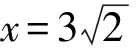
如果我们把第(Ⅰ)题的结论记为结论Ⅰ,教师可再引导学生展开联想,探究△PAB的垂心、重心、外心的轨迹.
探究2△PAB的垂心轨迹的探究.
易知△PAB的垂心轨迹在过点P且垂直于AB的定直线上(如图3所示).

图3
探究3△PAB的重心轨迹的探究.
不难得到:△PAB的重心轨迹在一条定直线上(如图4所示).

图4
探究4△PAB的外心轨迹的探究.
不难得到:△PAB的外心在一条定直线上(如图5所示).
探究2、3、4的证明,文[1]均给出,这里不再赘述.

图5
探究5结论Ⅰ的逆命题的探究
为了进一步探究结论Ⅰ的本质,教师可向学生提出如下问题:

利用《几何画板》的计算和动画功能,教师在事先做好的课件上进行演示性实验:
观察演示变化结果,由此得出结论:当点P(x0,y0)是定点时,直线AB的斜率必是定值.
证明如下:

图6
设A(x1,y1),B(x2,y2),PA的斜率为k,则PB的斜率为-k.
则PA的方程为y-y0=k(x-x0),
消去y并化简得
(a2k2+b2)x2-2a2k(kx0-y0)x+
a2(y0-kx0)2-a2b2=0,


探究6探究5的探究.
教师在事先做好的课件上再次进行演示性实验,可得如下结论:

证明如下:
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),AB与CD相交于点P(x0,y0),AB的斜率为k.
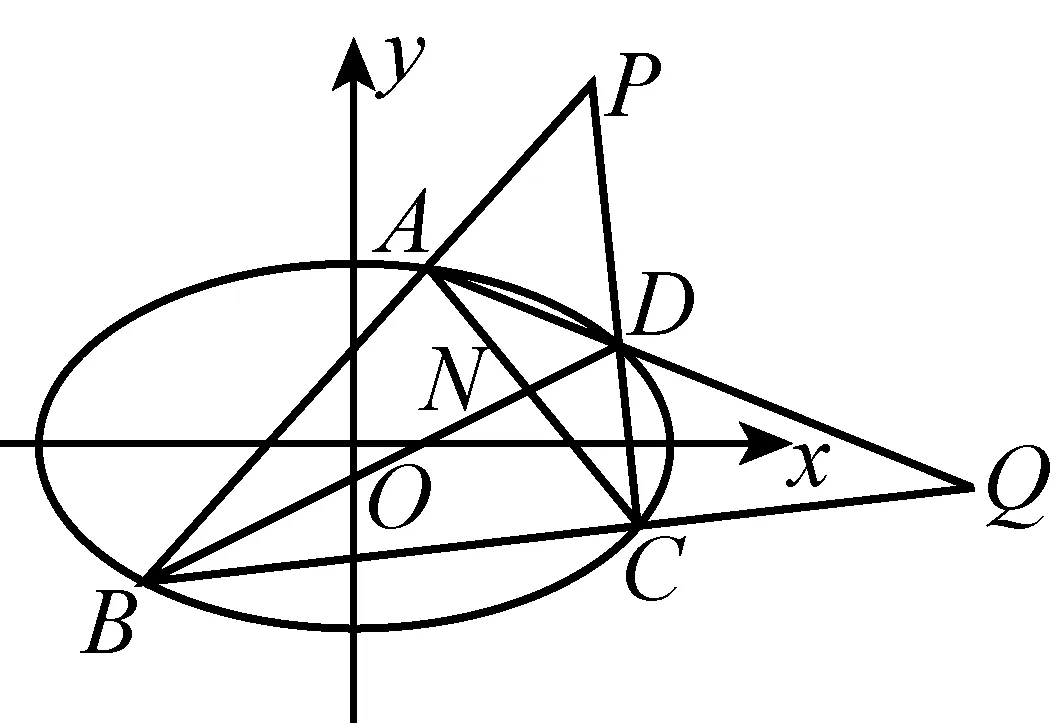
图7
(a2k2+b2)x2-2a2k(kx0-y0)x+
a2(y0-kx0)2-a2b2=0,
(1)
通过代入计算可得(1)式=0.
从而kAD=-kBC即AD与BC的斜率互为相反数.
由上面的证明过程中的(1)式可看出:将C、D两点横坐标x3、x4对调,结果不变,故对角线AC与BD的斜率也互为相反数.
探究7探究5的再探究
受探究6的启发,学生运用《几何画板》的度量、计算和动画功能,继续做实验,发现如下结论:

并证明如下:
设P(x0,y0),AB的参数方程为:
其中t为参数,θ为直线AB的倾斜角.
所以|PA|·|PB|=|t1t2|
所以|PA|·|PB|=|PC|·|PD|.
注:①若四边形ABCD的边AD与BC相交于Q,对角线AC与BD相交于点N,可得:
|QD|·|QA|=|QC|·|QB|,
|NA|·|NC|=|NB|·|ND|.
②由|PA|·|PB|=|PC|·|PD|易得:△PAD与△PCB相似且四边形ABCD的四个顶点共圆,因此,证明探究7中的结论时,也可先证明四边形ABCD的四个顶点共圆.
3 问题的再探究
在师生通过“数学实验”的手段得出7个结论后,还应该将探究从课内延伸到课外.此时,教师可将相应的数学实验平台搭建好,并指导学生运用类比的方式,继续探究以上结论在圆、双曲线、抛物线中是否也成立?进一步,可向学生提出:能否利用《几何画板》强大的度量、计算和动画功能,去发现问题中与面积有关的结论?然后再将你“发现”的结论一一加以证明.
我们常说,发现问题,能获取新的知识,能推动学科向前发展.所以,很多时候“发现问题”比“解决问题”更重要.在探究和发现问题的过程中,仅有演绎推理是远远不够的,因为在探究过程中常常需要“类比与归纳”,而合理的“类比与归纳”则往往需要大量的个例作为实验基础,因此,在中学课堂教学中引入“实验数学”是十分必要的.可以说,有了“实验数学”的课堂教学,才是全面、优质高效的教学.
