幂的逆运算常见类型分析

宋沧儒

(甘肃省民乐县第四中学　734500)

幂的运算是整式乘除法的基础，常见幂的运算法则有：

(1)同底数幂相乘的法则:am·an=am+n；

(2)幂的乘方的法则：(am)n=amn；

(3)积的乘方的法则：(ab)n=anbn；

(4)同底数幂相除的法则:am÷an=am-n(a≠0，m、n为正整数).

灵活逆用幂的这四条法则是一种常用的数学思维．巧妙运用这种数学思维解决有关幂的计算问题，常可使问题得到简捷解决，起到意想不到的效果．下面通过举例说明它在六个方面的具体应用．

一、求代数式的值

1.同底数幂乘法的逆运算

例1若1+2+3+…+n=a，求代数式(xny)(xn-1y2)(xn-2y3)…(x2yn﹣1)(xyn)的值．

分析根据同底数幂的乘法法则，同底数幂相乘，底数不变，指数相加，即am·an=am+n计算即可．

解答：原式=xny·xn-1y2·xn-2y3·…·x2yn-1·xyn

=(xn·xn-1·xn-2·…·x2·x)·(y·y2·y3·…·yn-1·yn)=xaya．

2.幂的乘方的逆运算

例2已知：274×93=3x,求x.

分析由于未知数x是方程右边部分3的指数，只要将方程左边部分也化为底数为3的幂的形式即可.

解答：274×93=(33)4×(32)3=312×36=318.

∵274×93=3x,∴318=3x,∴x=18.

3.积的乘方的逆运算

例3计算：(-0.125)11×811

分析将积的乘方公式逆用，即若有指数相同的幂相乘，则可将底数相乘，相同的指数作为共同的指数.再利用“积的乘方公式的逆计算”进行简化运算.

解答：(-0.125)11×811=(-0.125×8)11=(-1)11=-1.

4.同底数幂相除的逆运算

例4若xm+2n=16，xn=2，求xm+n的值．

分析根据同底数幂的除法，底数不变指数相减得出xm+2n÷xn=xm+n=16÷2=8．

解答：∵xm+2n÷xn=xm+n=16÷2=8，∴xm+n的值为8．

5.混合法则的逆运算

例5若2m=5，2n=6，则2m+2n=．

分析考查幂的乘方与积的乘方，先逆用同底数幂的乘法法则把2m+2n化成2m·2n·2n的形式，再把2m=5，2n=6代入计算即可．

解答：∵2m=5，2n=6，∴2m+2n=2m·(2n)2=5×62=180．

二、简化实数计算

分析根据幂的乘方法则,逆用积的乘方法则.

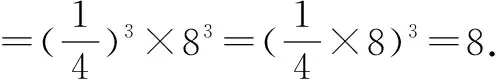
三、比较大小

例7比较下列一组数的大小:8131，2741，961.

分析先对这三个数变形，都化成底数是3的幂的形式，再比较大小．

解答：∵8131=(34)31=3124,2741=(33)41=3123,961=(32)61=3122,

∴8131>2741>961．

四、求因数

例8已知366-9能被80-90之间的两个整数整除，求这两个整数．

分析逆用幂的运算法则第一条将原数进行分解，就可找到解决此题的途径．

解答：∵366-9=366-32=9×(364-1)=9(332+1)(332-1)=9(332+1)(316+1)(38+1)(34+1)(34-1)=9(332+1)(316+1)(38+1)×82×80，∴这两个数是82、80．

五、确定个位数字

例9求3100-1的末尾数字．

分析先逆用幂的运算法则第二条，确定3100的末尾数字．

解答：∵3100-1=(32)50-1=950-1=(92)25-1=(81)25-1，而(81)25的个位数字是1，∴3100-1的末尾数字是0．

六、寻找参数

例10已知：0.254×209×0.01÷(5×108)=m×10n(1≤m<10)．求m、n的值．

分析逆用幂的运算法则，把等式的左边也转化成科学记数法的形式，便可求出m、n的值．

解答：原式=0.58×208×20×10-2÷(5×108)=108×20×10-2÷(5×108)=20×106÷(5×108)=4×10-2=m×10n．∴m=4，n=-2.