两共焦抛物导体柱板间的电势和电场

贾秀敏

(河北科技大学 理学院， 河北 石家庄 050018)

如图1所示，由于长直共轴共焦抛物导体柱板在空间产生的电场与轴无关，是垂直于轴的横截面上的二维场问题.文献[1-3]分别采用抛物柱坐标、高斯定理和复势函数法对此问题进行了研究；文献[4]采用不同坐标系的度规系数简化求解拉普拉斯方程.本文引入导体曲面函数，将解偏微分方程问题转化为一般的积分运算，简便直观地导出了共轴共焦抛物导体柱板间的电场分布.

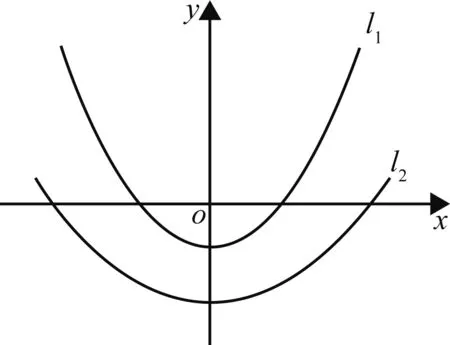
图1 共焦共轴抛物柱板Fig. 1 Two confocal parabolic conductor plates

1 解拉普拉斯方程

设f(x,y,z)为具有连续一、二阶偏导数的函数，c为参数，则

f(x,y,z)=c

(1)

表示一空间曲面族[5].若任取2个满足f(x,y,z)的薄导体曲面并带电，则曲面间的电势u满足拉普拉斯方程，而该电势在薄导体曲面上的取值为常量，说明电势u是f(x,y,z)的函数.

因为

所以

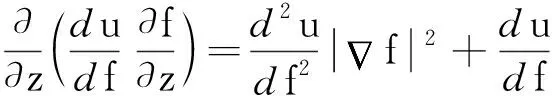
积分2次得曲面间的电势

(2)

其中，A、B为积分常数.

2 抛物板间的电势分布

(3)

其中抛物板l1对应c=c1，电势为u1；抛物板l2对应c=c2，电势为u2，由于板间电势u满足拉普拉斯方程，故将相应参量代入式(2)，即可计算抛物板间的电势.

(4)

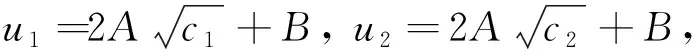
所以

(5)

式(5)给出的两抛物导体柱板间的电势分布与文献[1] 结果相同.

3 抛物板间的电场强度

(6)

由式(6)可得电场线满足微分方程:

(7)

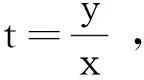
两边积分得

即

(8)

式(8)即为抛物柱板间的电场线方程.

由式(6)可知，柱板间电场强度大小为

(9)

故抛物板上电荷面密度为

(10)

说明抛物导体板上的电荷分布是不均匀的，越靠近抛物柱弧顶，电荷密度越大，而在较远处，电荷密度几乎为0.

通过导体曲面函数，利用积分导出了共轴共焦的抛物导体柱板间的电场分布，并给出了导体板上的电荷分布情况.该方法为计算等势面规范的带电导体产生的电场提供了新思路，有利于对静电问题的研究.