Cr掺杂LiZnAs稀磁半导体的第一性原理研究
2018-07-13张云丽朱自强李晓川刘奎立巫洪章周小东
张云丽,朱自强,李晓川,刘奎立,巫洪章,周小东
(1. 周口师范学院 物理与电信工程学院, 河南 周口 466001; 2. 周口师范学院 稀土功能材料及应用实验室, 河南 周口 466001; 3. 周口师范学院 机械与电气工程学院, 河南 周口 466001)
0 引 言
稀磁半导体是指非磁性半导体中的部分原子被过渡金属元素取代后形成的磁性半导体,兼具半导体和磁性性质,能同时利用电子的电荷和自旋属性[1],具有巨磁阻效应、显著的磁光效应、反常霍尔效应等优越性能,被认为是21世纪的重要材料,是近年来国内外研究的热点[2-3].与传统半导体器件相比,稀磁半导体自旋电子器件具有体积小、速度快、能耗低等诸多优点[4],在半导体集成电路、高密度非易失性存储器、半导体激光器、磁感应器和光隔离等领域具有广阔的应用前景,因此稀磁半导体已成为信息技术、材料学等领域值得深入探究的课题.
Zn-As基稀磁半导体不仅结构类型多、材料丰富[5-14],而且与其对应的同构Fe-As基超导体有可匹配的晶格参数,为设计基于磁性、半导体和超导体的异质结构[6],探索新的物理效应和应用特性提供了重要可能.新合成的稀磁半导体 Li1.1(Zn1-xCrx)As (x= 0.1) 最大居里温度较高,为218 K,因此,理论研究Li1.1(Zn1-xCrx)As有重要意义.虽然理论上WANG等[15]和TAO等[16]都研究了Cr掺杂LiZnAs体系的电子结构和磁性特征,但一定的Li过量、Cr掺杂浓度下,当Cr原子之间的初始距离一定时,并未对过剩的Li空位之间的距离对其构型稳定性的影响以及磁性原子的轨道磁矩进行研究. 本文的主要目的及亮点是在一定的Li过量、Cr掺杂浓度下,当Cr原子之间的初始距离一定时,研究过剩的Li空位之间的距离对Cr掺杂LiZnAs体系构型稳定性的影响、体系磁性主要来自哪种原子的哪个轨道以及Cr掺杂LiZnAs体系的电子结构.
1 结构模型和计算方法
1.1 结构模型
LiZnAs的晶体结构如图1所示,属于反萤石结构[10-12],空间群为F-43 m.晶格常数为a=b=3.776 Å,c=6.349 Å,且α=β=γ=90°.在构建LiZnAs模型[5, 15]时,类似GaAs结构构建ZnAs二元复合,在邻近As原子四面体间隙填上Li原子.As原子呈立方密堆积,Zn原子和Li原子填充在四面体间隙中,As原子的配位数为4,Zn原子和Li原子配位数为8. LiZnAs晶体结构原胞中,有4个As原子、4个Li原子和4个Zn原子.
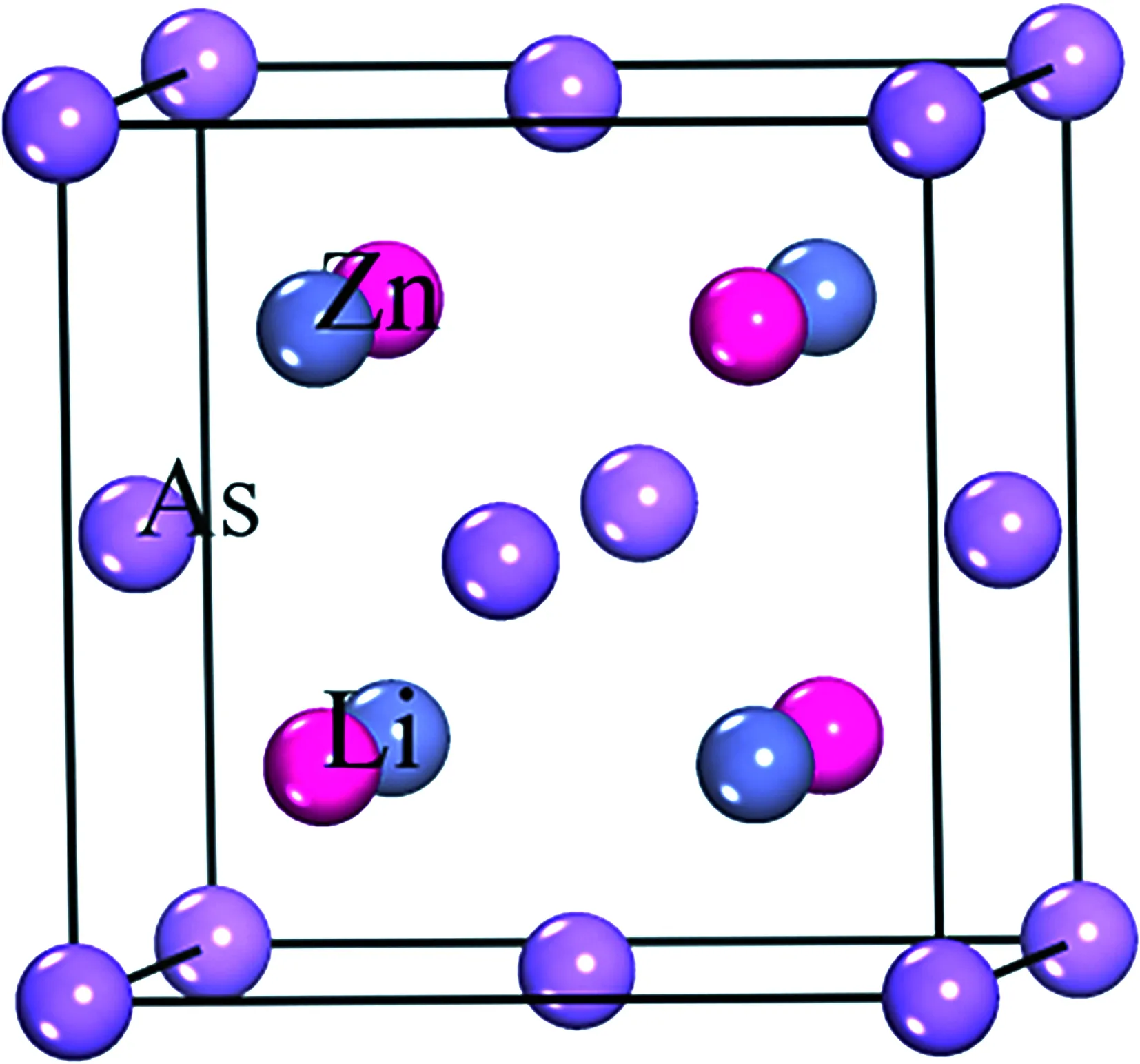
图1 LiZnAs晶体结构Fig. 1 The crystal structure of LiZnAs
为了得到实验要求的掺杂浓度范围,首先构造了5×1×1超晶胞结构(见图2),在图2中,Cr掺杂LiZnAs会形成多种构型,本文只研究在过量Li下掺入Cr原子的情况.为比较掺杂Cr及过量Li原子位置对稳定性的影响,图3给出了掺杂后可能得到的5种不同构型.图3中黄色的2个为过量的Li原子,在(a)、(b)、(c)3种晶体构型中,2个Cr原子替代Zn原子的位置相同,且(a)、(b)、(c)3个构型中掺杂的Cr原子距离一样;(a)和(b)中过量的2个Li原子距离也相等,但(c)构型中的2个过量Li原子距离较远;(d)、(e)2种构型中2个Cr原子替代Zn
图2 LiZnAs的5×1×1超胞模型Fig. 2 The 5×1×1 super cell model of LiZnAs
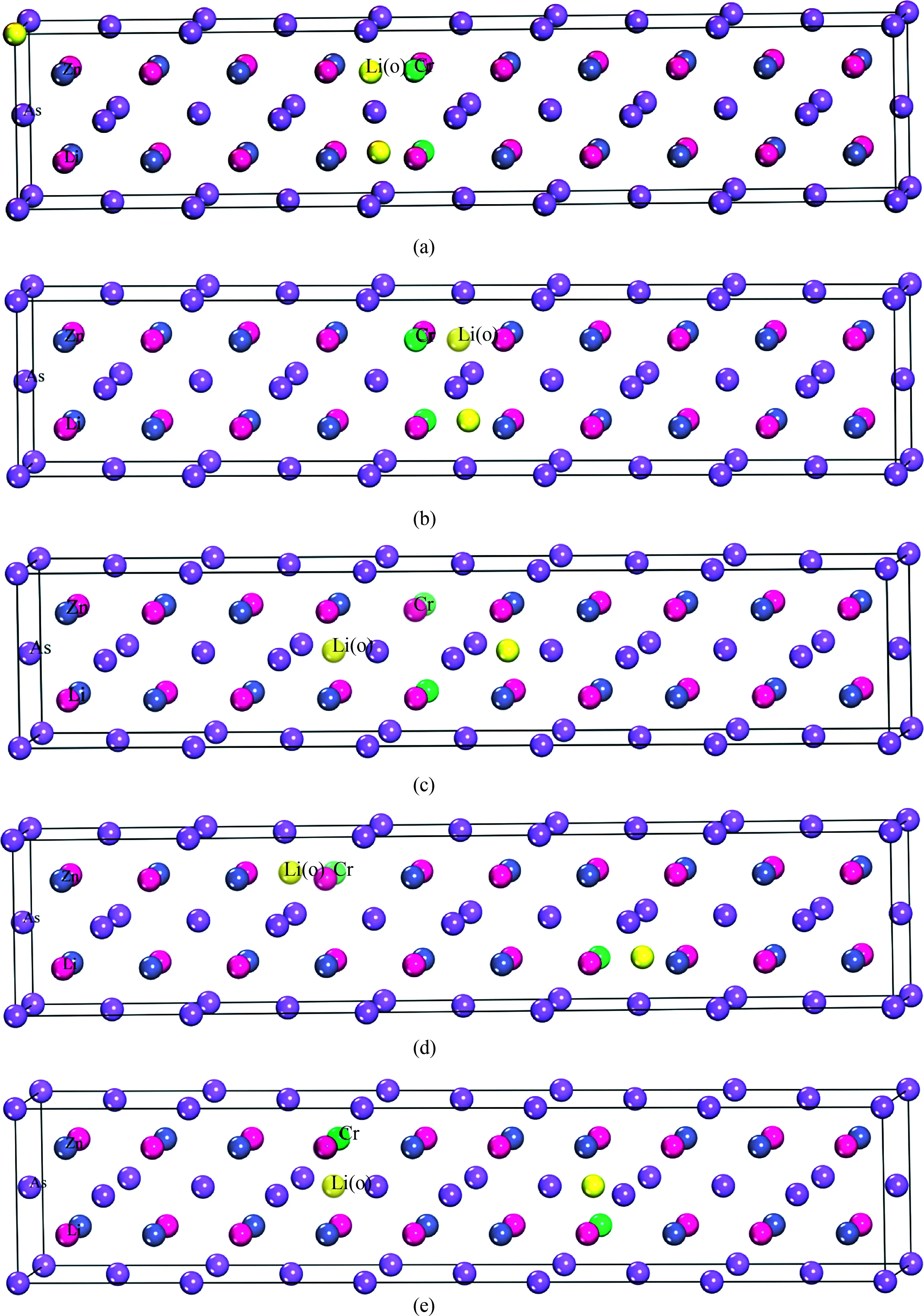
图3 Li1.1Zn1-xCrxAs(x= 0.1)的晶体结构图Fig. 3 The crystal structure of Li1.1Zn1-xCrxAs(x= 0.1)
原子的位置相同,且掺杂的Cr原子距离相同,但(d)中Li原子的距离较远.
1.2 计算方法
运用基于密度泛函理论模拟的软件包VASP[17]进行计算.使用PAW(projector augmented-wave)[18]下的PBE (perdew-burke-ernzerh)[19]赝势来处理体系的交换相关式,计算过程中,选取平面波截断能Ecut=500 eV,K点由Monkhorst软件自动得到[20].计算中,K点分别取1×5×5和2×10×10 的Monkhorse-Pack网格,以优化结构,改善电子结构性质.
2 计算结果与讨论
2.1 Cr掺杂LiZnAs的稳定构型
为得到一定掺杂浓度下Cr掺杂LiZnAs体系的稳定构型及掺杂原子位置对体系稳定性的影响,对图3中给出的Cr掺杂LiZnAs形成的5种构型进行了结构优化,并计算优化后的结构能量、优化前过量的Li(O)之间的距离(dLi(O)- Li(O))和掺杂的Cr之间的距离(dCr-Cr),结果如表1所示. 比较表1中图3(a)~(e) 5种构型下的能量可知,Li1.1Zn1-xCrxAs(x= 0.1)体系在3(c)构型下能量最低,最稳定.
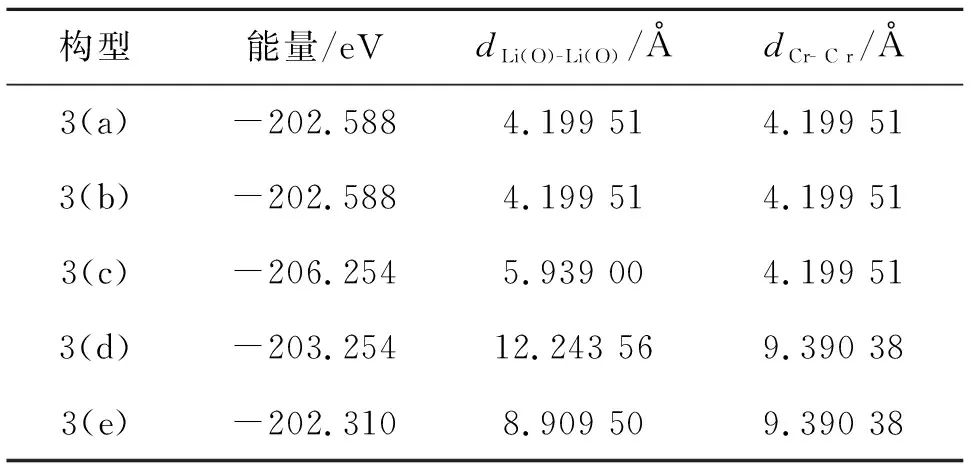
表1 Li1.1Zn1-xCrxAs(x= 0.1)在不同构型下的能量、结构优化前过量Li(O)之间的距离(dLi(O)-Li(O))和掺杂的Cr之间的距离(dCr- Cr)
进一步分析可知,(a)和(b)构型下的能量相等,同时,结构优化前过量的Li(O)之间的距离(dLi(O)- Li(O))和掺杂的Cr原子之间的距离(dCr- Cr)亦相等,可见Li1.1Zn1-xCrxAs(x= 0.1)主要受优化前dLi(O)- Li(O)和(dCr- Cr)的影响.3(c)构型较3(b)构型能量低3.666 eV,说明在优化前掺杂的Cr间距离(dCr-Cr)相等的情况下,过量Li(O)之间的距离(dLi(O)- Li(O))越大,Li1.1Zn1-xCrxAs(x= 0.1)体系能量越低,越稳定;3(d)构型较3(e)构型能量低0.944 eV,进一步证实当优化前掺杂的Cr之间的距离(dCr- Cr)相等时,过量Li(O)之间的距离(dLi(O)- Li(O))越大,Li1.1Zn1-xCrxAs(x= 0.1)体系的能量越低,越稳定;但随着优化前掺杂的Cr之间的距离(dCr- Cr)增大,过量Li之间距离(dLi(O)- Li(O))的变化对体系总能的影响减小.
2.2 Cr掺杂LiZnAs的磁性来源
迄今未见关于稀磁半导体磁性起源的统一理论,因此,理论研究Cr掺杂LiZnAs体系的磁性来源很有必要.通过计算稳定构型下Li1.1Zn1-xCrxAs(x= 0.1)体系的磁性,发现稳定构型(图3(c))下Li1.1Zn1-xCrxAs(x= 0.1)体系的总磁矩为9.528 μB,其中一个Cr原子的总磁矩为3.899 μB,大于实验预测值的2~3 μB[10],这由计算所用的理论是基态理论而实验体系并非处于基态导致.由于图3(c)的晶体结构中,1个超晶胞含有2个Cr原子,因此,在超晶胞中,Cr原子的总磁矩为3.899 × 2 =7.798 μB,最稳定构型的Li1.1Zn1-xCrxAs(x= 0.1)晶体模型磁矩主要来自Cr原子,与实验中发现的Li1.1Zn1-xCrxAs(x= 0.1) 体系中Cr取代Zn引入自旋、过量的Li提供P型载流子的结论一致[10].为深入研究Cr原子的磁性主要来自哪个轨道,表2列出了Cr原子s,p,d轨道的轨道磁矩,其值分别为0.061, 0.084, 3.753 μB, 通过比较可知,Cr原子的s,p轨道几乎无磁矩,Cr原子的磁矩几乎全部来自3d轨道.可见Cr掺杂的LiZnAs晶体的最稳定构型的磁性主要来自Cr原子的3d轨道.

表2 Cr原子在Li1.1Zn1-xCrxAs(x= 0.1)稳定构型中各轨道的磁矩
2.3 Cr掺杂LiZnAs的电子结构
为比较 Cr掺杂LiZnAs对体系电子结构的影响,图4(a)和(b)分别给出了LiZnAs和最稳定构型下Li1.1Zn1-xCrxAs(x= 0.1)的电子结构图.从图4(a)可以看出,无任何掺杂的LiZnAs,总态密度图上下对称,体系不具有磁性,在费米面(EF= 0 eV)上,LiZnAs晶体总的态密度为0,显示了其半导体特性,计算的带隙大小为1.16 eV,小于实验中LiZnAs的带隙值1.62 eV[21]和1.25 eV[22]. 计算结果偏低的原因是基于局域密度近似的密度泛函理论计算往往低估了体系的禁带宽度[23],但这并不影响对LiZnAs及Li1.1Zn1-xCrxAs(x= 0.1)计算结果的理论分析.由图4(b)可知,基于最稳定构型的Cr掺杂LiZnAs晶体结构,总态密度在-6~6 eV的已完全不具有对称性,在费米面上自旋向上的态密度不为0,说明自旋向上的态密度具有金属特性,同时自旋向下的态密度显示
了半导体特性.由此可知,Li1.1Zn1-xCrxAs(x= 0.1)具有稀磁半导体特性,与实验结果[10]及理论计算结果[15-16]基本一致.事实上,文献[16]还研究了只有Cr掺杂的LiZnAs体系LiZn1-xCrxAs,发现其并无磁性,可见Li过量是导致Li1.1Zn1-xCrxAs(x= 0.1)体现磁性的原因.
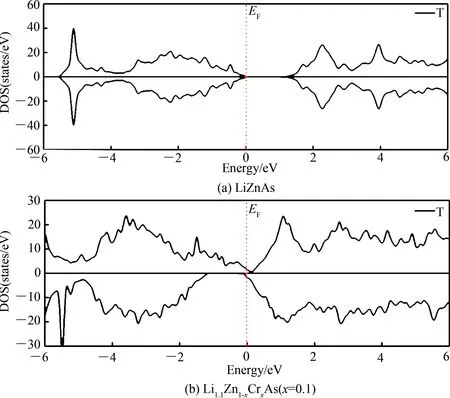
图4 Li1.1Zn1-xCrxAs(x= 0,0.1)的电子结构图Fig. 4 The electronic structures of Li1.1Zn1-xCrxAs(x= 0,0.1)
为进一步研究Li1.1Zn1-xCrxAs(x= 0.1)最稳定构型的电子结构,图5给出了其各元素原子的分波态密度.图5(a)~(d)显示,Li1.1Zn1-xCrxAs(x= 0.1)体系中各原子分态密度不具有对称性.在-6~-4 eV能量内,自旋向上及向下的态密度都主要来自于Zn原子的4s态和As原子的2p态;在-4~-2 eV能量内,自旋向上(向下)的态密度主要来自于Cr原子的3d态、Zn原子的3p态和As原子的2p态;在-2 ~0 eV能量内,自旋向上的态密度主要来自于Cr原子的3d态和As原子的2p态,自旋向下的态密度几乎为0.在0 ~2 eV能量内,自旋向上(向下)的态密度主要来自于Zn原子的4s态和Cr原子的3d态;在2 ~6 eV能量内,自旋向上(向下)的态密度主要来自于Li原子的2p态、Zn原子的3p态、As原子的2p态以及Cr原子的3d态.通过对比图5中各原子、各轨道态密度的对称性发现,费米面附近Cr原子3d轨道态密度对称性最低,进一步说明Li1.1Zn1-xCrxAs(x= 0.1)的磁性主要来自于Cr原子的3d轨道.为更有力地说明Li1.1Zn1-xCrxAs(x= 0.1)的磁性主要来自于Cr原子的3d轨道,图5(e) 给出了Cr-3d的空间电子分波态密度, 结果显示Cr-3d的空间电子分波态密度dxz, dyz,dz2,dx2-y2,dxy,在费米面以下,主要对自旋向上的态密度有贡献;在费米面之上,主要对自旋向下的态密度有贡献,且dxz, dyz的态密度几乎是重合的,dz2,dx2-y2曲线的变化趋势一致.此结果进一步证实Cr掺杂LiZnAs的磁性主要来自于Cr原子的3d轨道.
3 结 语
采用密度泛函理论(DFT)框架下的第一性原理的计算方法,研究了Li过量情况下Cr掺杂的LiZnAs稀磁半导体体系.首先,通过比较不同构型下Cr掺杂LiZnAs体系的能量得到稳定构型,并得到当掺杂Cr原子距离一定时,过量Li原子距离越大体系能量越低且越稳定的结论;其次,进一步研究发现,Cr掺杂LiZnAs磁性主要来自于Cr原子的3d轨道;最后,计算得到Cr掺杂LiZnAs稀磁半导体体系的电子结构具有稀磁半导体的特性.且由分波电子态密度,进一步说明Li1.1Zn1-xCrxAs(x=0.1)的磁性主要来自于Cr原子的3d轨道.
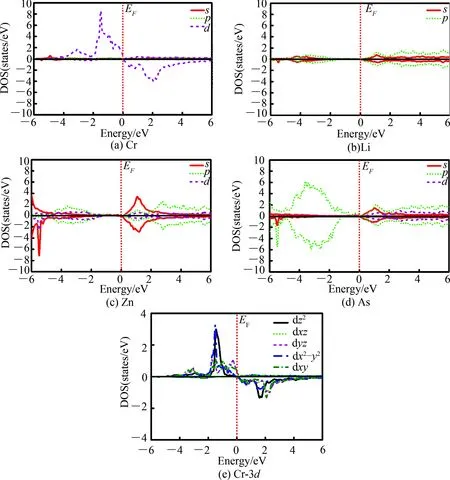
图5 Li1.1Zn1-xCrxAs(x= 0.1)体系的分波电子态密度Fig.5 The partial wave electronic density of states of Li1.1Zn1-xCrxAs(x= 0.1)

