数列求和的七种基本方法
2018-07-12甘志国
甘志国
(北京丰台二中 100071)
一、运用公式法
很多数列的前n项和Sn的求法,就是套等差、等比数列前n项和Sn的公式,因此以下常用公式应当熟记:
还要记住一些正整数的幂和公式:
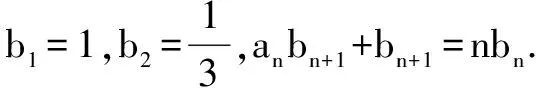
(1)求{an}的通项公式;
(2)求{bn}的前n项和.

又因为{an}是公差为3的等差数列,所以an=2+3(n-1)=3n-1.


二、倒序相加法
事实上,等差数列的前n项和Sn的公式推导方法就是倒序相加法.
题2求正整数m与n(m 解显然,这些既约分数为: 所以2S=(m+n)·2(n-m)=2(n2-m2),S=n2-m2 题3求数列{1+2+3+…+n}的前n项和Sn. 解法2因为 所以 解法3(倒序相加法)可得 Sn=1+(1+2)+(1+2+3)+…+(1+2+3+…+n), Sn=1+(2+1)+(3+2+1)+…+[n+(n-1)+(n-2)+…+1], 把它们相加,可得 3Sn=1(n+2)+2(n+2)+3(n+2)+…+n(n+2) 题5(2017年高考全国卷Ⅲ文科第17题)设数列{an}满足a1+3a2+…+(2n-1)an=2n. (1)求{an}的通项公式; 解(1)当n≥2时,可得 a1+3a2+…+(2n-1)an=2n, a1+3a2+…+(2n-3)an-1=2(n-1). 把它们相减后,可得 由题设还可得a1=2,从而{an}的通项公式为 由(1)的答案,可得 题7(2017年高考天津卷第18题)已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4. (1)求{an}和{bn}的通项公式; (2)(理)求数列{a2nb2n-1}的前n项和(n∈N*). (文)求数列{a2nbn}的前n项和(n∈N*). 解(1)(过程略)an=3n-2,bn=2n. (2)用错位相减法可求得答案: (文)(3n-4)×2n+2+16. 题8(2017年高考山东卷文科第19题)已知{an}是各项均为正数的等比数列,且a1+a2=6,a1a2=a3. (1)求数列{an}通项公式; 解(1)(过程略)an=2n. 又因为S2n+1=bnbn+1,bn+1≠0,所以bn=2n+1. 题9数列{(2n-1)·3n}的前n项和Sn=. 解设等差数列{am}的公差为d,等比数列{bm}的公比为q(q≠1),得 am·bm=[a1+(m-1)d]·b1qm-1(m=1,2,…,n). 先用错位相减法求数列{am·bm}的前n项和Sn: Sn=b1{a1+(a1+d)q+(a1+2d)q2+…+[a1+(n-1)d]qn-1}, qSn=b1{a1q+(a1+d)q2+…+[a1+(n-2)d]qn-1+[a1+(n-1)d]qn}. 所以有下面的结论成立:若{am},{bm}分别是等差数列、等比数列(其公比q≠1),且a1,b1均是与n无关的常数,则数列{am·bm}的前n项和Sn=(an+b)qn-b,其中a,b是与n无关的常数. 由此结论就可以用待定系数法快速求解本题: 可设Sn=(an+b)·3n-b(其中a,b是常数). 可得S1=3,S2=3+27=30, 从而Sn=(n-1)·3n+1+3. 题10求和Sn=1·2n+2·2n-1+3·2n-2+…+(n-1)·22+n·2. 解得 (3)求数列{(2n-1)·3n}的前n项和Sn. 解(1)当x=0时,显然成立.当x≠0时,由等比数列的前n项和公式知,欲证结论也成立. (2)视(1)的结论为两个函数相等,两边求导后即得欲证成立. (3)(2n-1)·3n=6(n·3n-1)-3n. 题12(2008年高考江苏卷第23题)请先阅读:在等式cos2x=2cos2x-1(x∈R)的两边对x求导,得(cos2x)′=(2cos2x-1)′. 由求导法则,得(-sin2x)·2=4cosx·(-sinx),化简后得等式sin2x=2sinxcosx. (2)对于整数n≥3,求证: 答案:(1)在已知等式两边对x求导后移项可得欲证. (2)①在结论(1)中令x=-1可证. ③在已知等式两边在[0,1]上对x积分后可得欲证.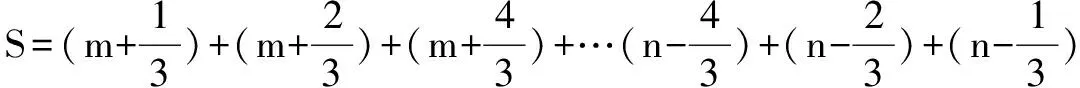
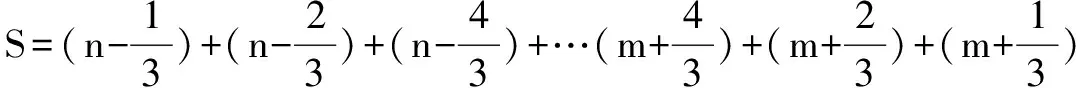
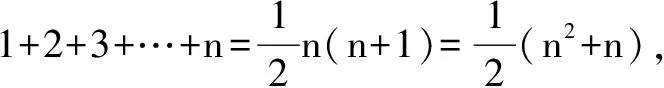
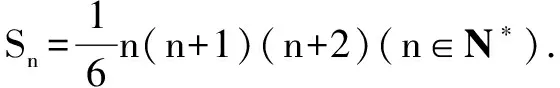
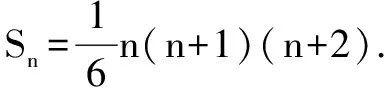
三、裂项相消法

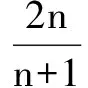


四、分组求和法
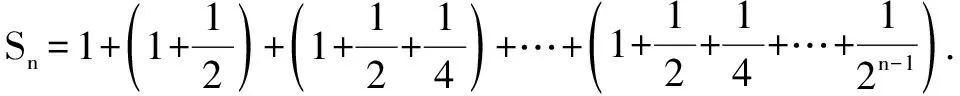

五、错位相减法
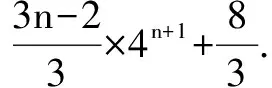

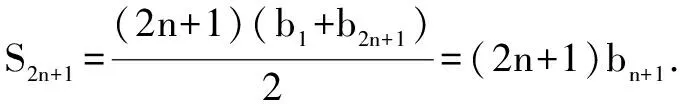
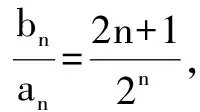
六、待定系数法

七、求导法、积分法