分数应用题教学初探

文 鹤山市玉桥小学　林凤玲

分数应用题是小学应用题教学的重点，也是难点。现就教学分数应用题的过程中的一些感受谈谈我个人的点滴体会：

一、抓住特征，用普遍存在的数量关系解答一般应用题

解答分数应用题要抓住一个显著特点：就是每一个具体的实际数量对应着一个分率 （几分之几或百分之几）。同样，每一个分率也总有一个具体的实际数量与它相对应，所以解答分数应用题，一定要找准单位 “1”和对应分率这 “两件宝”（找已知量的对应分率或找已知分率的对应数量）。

根据这一普遍特征，在分数应用题中，它总是存在有以下的数量关系：

（1）单位“1”的量×对应分率=对应数量；

（2）对应数量÷单位“1”的量=对应分率；

（3）对应数量÷对应分率=单位“1”的量。

因此，对于一般的分数应用题，我们应该先找出题目中单位“1”的量是什么，已知条件属于什么，要求的问题又属于什么，然后对照以上的数量关系，确定解答所用的运算方法，看看要求的问题所必备的条件是否已经完全具备。如果欠缺条件，又要通过什么方法把它找出来。例如，在解答 “我校科技兴趣小组一共做了40件车模和船模，其中是船模，做了车模几件？”这个题目的时候，我们可以分析：在这个题目中，单位 “1”的量是所做的车模和船模的总数，是一个已知量，要求的问题是部分数量是多少，但这部分数量所占单位“1”的分率还不知道，我们只知道与这个部分数量共同组成单位 “1”的另一部分数量是占了总数的，那么要求的这部分数量的对应分率就应该是找出对应分率后，再根据第 （1）个数量关系式，求得所要求的问题。

二、加强针对性训练，提高解题准确率

1.重视作线段图训练

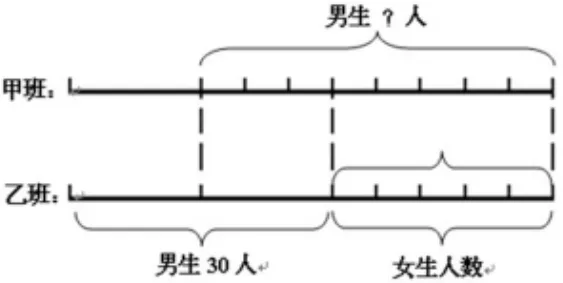
分数应用题比较抽象，借助线段图能够帮助学生弄清有关数量关系，找到解题的途径。作图的基本方法：先画表示单位 “1”的线段，注意线段的规范性 （要完整、简明、清晰、比例适当），以及作图的灵活性，运用补、截、移、叠等作图技巧，讲究作图的科学性。同时引导学生认真看图，分析思考，理解数量关系，使学生的思维与作图同步进行。这样就能充分发挥线段图的直观启示作用。例如：甲班和乙班人数相等。甲班女生人数相当于乙班男生人数的；乙班女生人数相当于甲班男生人数的已知乙班有男生30人，甲班有男生多少人？由于条件的叙述婉转含蓄，造成学生解题的困难。这时可引导学生作图：画图时，如果把甲班的男生部分与乙班男生部分画在同一侧，则不容易显现出数量关系，难以解答。如果把互相比较的两个量画在同一边，如图，从图上容易看出，甲班男生人数的（1－）和乙班男生的相等。找到了解题的方法＝40 （人）。

2.重视变式对比训练

对于易混内容，有意识地设计一些似是而非的变式题组让学生练习、比较，分析它们的细微差别，从而掌握解题规律。如：比36吨少吨的数是多少？比36少的数是多少？

3.重视发散思维训练

发散思维是解决问题时沿着各种方向、不同途径去探索和思考。如应用题：修一条600米的公路，由甲队修需要20天，由乙队修需要30天。两队合修需要多少天？引导学生从一般工作问题和工程问题的不同角度去思考，得到不同的解法：

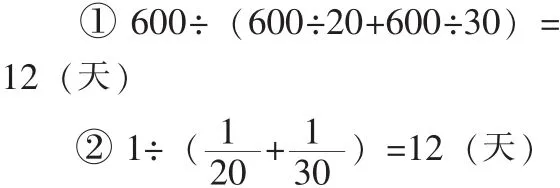
再加以比较，得出最佳解法②，在此基础上，让学生将 “600米”换成900米、3000米、1200米等，用两种方法求解，使学生明白 “600米”这个条件对于解法②是多余的。

三、归纳特性，运用不同思路分析较难的应用题

对于常见的较难的分数应用题，我们应该在分析题目存在普遍特征的基础上，找出题目的自身特征，从不同的角度运用不同的思路来分析、解答。

1.转化思路

在解答分数应用题过程中，确定单位 “1”是解答的关键，但有些分数应用题，会出现两个或两个以上不同的单位“1”，该怎么办呢？这时就需要根据实际情况，通过转化，把所有分率都统一为同一个单位 “1”再进行解答。

例如：甲、乙、丙三个修路队修一条公路，已知甲队修了这条公路全长的，乙队修了剩下的，丙队修了甲队的，还剩下10千米，这条公路全长多少千米？

分析：要求这条公路全长多少千米？如果我们能够找到剩下10千米的对应分率 （10千米占这条公路全长的几分之几），那么就可以解决这个问题了。

2.量不变的思路

量不变的思路是在解题时，我们善于在数量中找到不变量，确定单位 “1”的量，利用题目中某个不变量作为解题的突破口，分析这个不变量与其他量之间的关系，从而找出解题方法。

例如：甲桶比乙桶油多4.8千克。如果从两桶油各取1.2千克后，这时乙桶油相当于甲桶油的两桶油原来各重多少千克？

我们应该找出存在的一个不变数量 （两桶油相差的重量），利用这个数量与其他量之间的关系 （甲桶油与乙桶油的重量的差是现在甲桶油的1－），也就是找到了我们一般要找的对应数量和对应分率（单位“1”：甲桶油现在的重量），要求的问题也就迎刃而解。

3.假设思路

在这种类型的应用题中，一般会存在有两个或者两个以上不同种类的数量，它们之间既相互联系，又相互制约。这就要求在教学的过程中要假设其中的一个数量，再利用它们之间的联系与制约条件，确定另一个或几个数量与这个假设之间的关系，从而找出假设与题目条件存在的矛盾，把存在的矛盾作为解题的突破口，从而得到假设不存在的另一个量。

例如常见的鸡兔同笼类型问题：“某剧团租用影剧院进行表演，租期20天，表演一天纯收入5000元，休息一天付租场费1000元，该剧团共收入88000元，该剧团休息了几天？”在教学的过程当中，我们可以假设这20天全部工作，那么应得到的收入是100000元，但现在只有88000元，比应有的少了12000元，这就说明了假设不成立，也就是这20天里面有几天是休息的，每休息一天减少5000+1000=6000（元）收入，所以休息的时间为 12000÷6000=2 （天）