基于简正波的混响声压模型

查继林

(声纳技术重点实验室 第七一五研究所，杭州，310023)

混响是主动声呐工作的主要干扰源，因此有必要对混响信号进行仿真，以测试声呐的工作性能。传统点散射模型方法和单元散射模型物理意义清晰，但计算量较大[1]。本文结合单元散射模型，在简正波声强模型的基础上提出了一种基于简正波理论的声压模型，减小了计算量，且模型中傅里叶变换的应用使得该方法也适用于宽带发射信号。

1 声压模型

混响伴随着声呐发射信号而产生，与发射信号本身的特性和传播通道的特性有着密切的关系，是主动声呐主要的干扰因素。混响信号是由大量独立的散射体所产生的散射声在接收点叠加而形成的。对于海底混响，假设海底各散射单元之间是独立的，则t时刻混响信号可表示为[2]

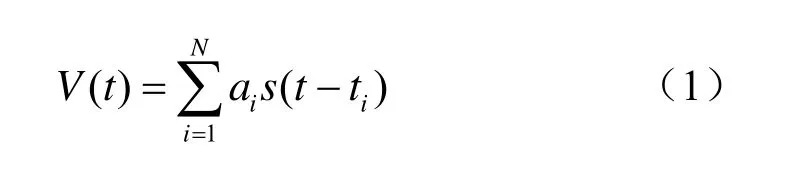
式中，s(t)是主动声呐发射波形，ti是第i个散射区域产生散射波形的时刻，αi表示该散射单元散射声波的振幅。αi、ti都与该散射单元距离声呐的水平距离有关。

假设第i个散射单元距离声源的水平距离为ri，对于平坦海底收发合置声呐，由简正波理论可知其反向散射回波在接收点的声压振幅为[3]

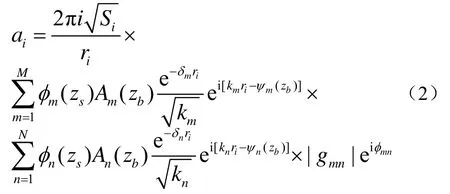
对于各阶传播模态，假设其群速度等于各阶模态的平均群速度，即（M为传播模态的阶数，为第m阶模态的群速度），则将αi、ti代入式（1）就得到了简正波混响的声压模型。

2 傅里叶变换模型

第1节中声压模型物理意义明确、计算简单，但对于远程混响，由不同阶次简正波相速度和群速度不相等引起的频散效应不能忽略。比如100 m海深、声源深度50 m，频率100 Hz，使用Kraken模型仿真可得，声源激发的传播模态为7阶，其最大群速度cg1=1 496.96 m/s，最小群速度cg7=1 322.13 m/s，5 000 m处散射回波相对于发射信号在时间上的扩展为0.88 s，波形发生严重畸变，必须重新计算散射回波。这时就必须借助傅里叶变换。

首先确定频率积分区间。积分区间取决于发射信号的频谱，实际中通常发射信号的能量集中在一个频率段内，在该频率段外的信号能量非常小，假设该频率段的最大值为ωmax。若距离为r，深度为z的点的声压随时间的变化为[4]

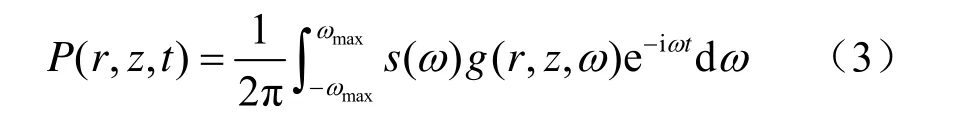
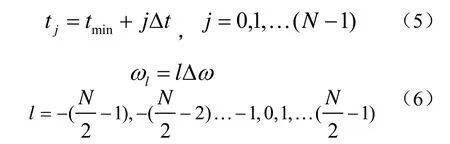
且频率采样间隔Δω和时域采样间隔Δt需满足这就直接决定了频率的采样间隔为使用累加来代替积分运算，然而根据标准采样理论，频率的离散化导致了时域周期为T的周期性，使得结果成为所有周期时移的和

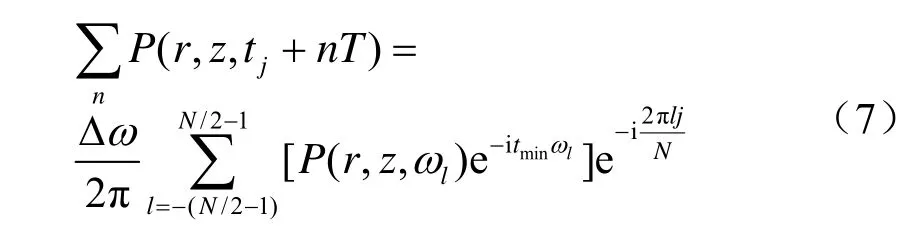
或者，根据傅里叶变换的共轭对称性质

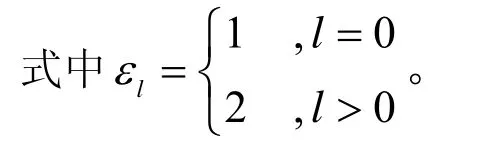
于是所选时间窗的实际响应就变成了

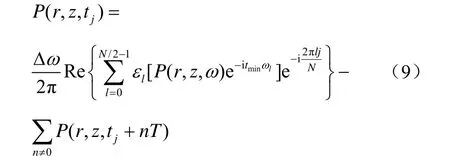
式中最后一项累加代表周期时间窗引起的“卷绕”和“混叠”。

选择2的整数次幂作为N，可以实现实序列快速傅里叶变换，同时对tj的所有N个值计算式的第一个求和式进行计算。

需要注意的是，我们并没有把频率采样和信号的最高频率成分联系起来，这是因为在离散求和代替连续傅里叶积分时出现了式（9）中最后求和项所表示的混叠。因为与FFT相关的计算量非常小，可方便选取表示所有接收点的响应所需要的时间窗的长度T和时域采样间隔Δt。频域抽样间隔可由其与时域采样间隔的关系得到。显然，为了保证频域积分区间能够包含所有的有效带宽，必须保证

由于式（9）出现了叠加项，因此时间窗的选择成为非常关键的问题。为了减小计算量，选择的时间窗要尽可能的短。时间窗的长度决定了频域采样间隔，较短的时间窗可以增大频域的采样间隔，从而减小累加项的个数，降低计算量。另一方面，时间窗又必须要选取的足够长，使得其能够包含所有接收点的全部瞬态响应从而消除混叠。瞬态响应的起始时间和持续时间受到声源发射信号的影响，还有海洋介质频散效应的影响。

合适的时间窗起始时间tmin可根据传播时间确定。因此，对于波导问题，对于时间窗的合适的起始时间的一种保守估计是使得起始时间tmin小于或者等于以该波导问题中最高波速传播的信号到达时间，即

如果我们按照上式选取tmin，那么时间窗的起始时间将会随距离而改变，实际上就变成了一个“活动”的时间窗。以最高水平速度cmax传播的波（比如首波），在按距离叠置的时间序列图中，将在相同的对比时间出现。实际中经常利用具有不同换算速度的对比时间叠置把具体的到达波与分层介质中的具体层次联系起来。

对于由主要模态控制的远程波导问题，一种合理的解决方法是在声源发射信号覆盖的频率范围内确定出最小的模态群速度umin，然后选择时间窗长度T使得在最远距离处的瞬时响应能够包含在该时间窗内，即

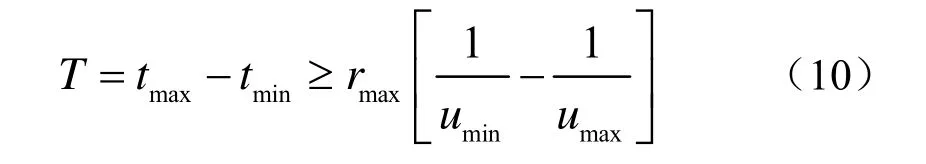
另外，对于那些声场主要是连续谱控制的近程问题，陡峭海底和海面的弹跳信号和他们的多次弹跳信号将会使接收信号产生“拖尾”。这种情况下，时间窗的长度T最好由“拖尾”和误差决定，即通过不断的增大T，直到产生稳定的结果。

一旦时间窗的长度T确定之后，就必须选择能够对信号进行合适采样的FFT点数N。根据实际需要，时域采样间隔比较合适的取值是使得每个周期有8个采样点，即

3 混响声压模型

根据以上内容描述，可以使用RFFT算法计算基于简正波的混响的声压模型，其算法如下所述：对于单频脉冲信号，频率为f0，脉冲时长τ0，假设混响的最远距离为rmax，则最远距离上散射单元的散射信号最先到达接收点的时间为各阶模态最大群速度，且散射回波持续时长为若系统采样频率则采样点数对发射信号作傅里叶变换，可得发射信号的频谱如果能够求得发射信号从声源到散射区域再到接收点的频率响应那么就可以利用傅里叶逆变换求得散射回波的时间序列假设声源深度zs，频率f0，水平距离ri处的散射单元散射回波为[4]

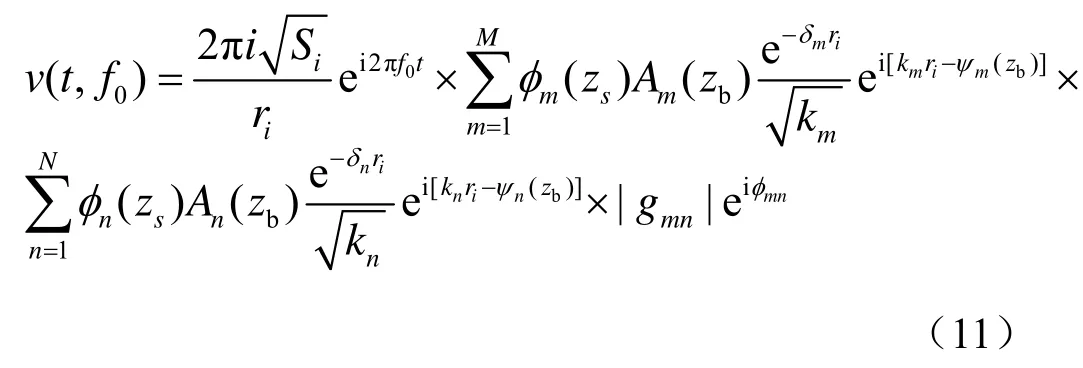
故其信道的频率响应为

如果将fs等分为N份，对每一个频率点计算便可得到N点频率响应在实际中接收到的混响信号总是实数，只需求解前N/2点的频率响应，取其共轭对称即可得到其后N/2点的频率响应。另外，实际中发射信号通常具有一定的带宽，只考虑发射信号有效带宽内的频率响应，可以进一步减小计算量。发射信号的N点傅里叶变换为S(k) ，则水平距离上的散射回波的频谱为所以水平距离ri处散射回波的时间序列将所有距离上的散射回波时间序列按照其对应的传播时延进行叠加，即可得到混响的简正波声压模型

式中ni为离散时延。使用Kraken计算各频点的传播衰减及群速度，仿真结果如图1～4所示。其中，图2为图1环境条件下声道的频率响应，仿真发射信号采用CW信号，其频谱如图3所示，图4即为仿真的声压信号。

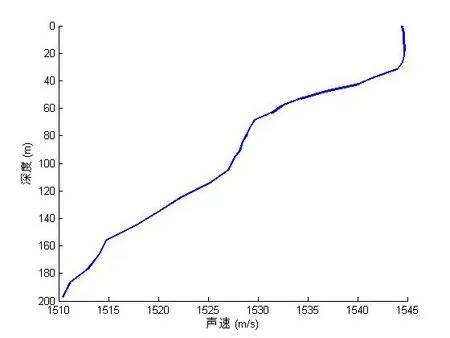
图1 声速剖面

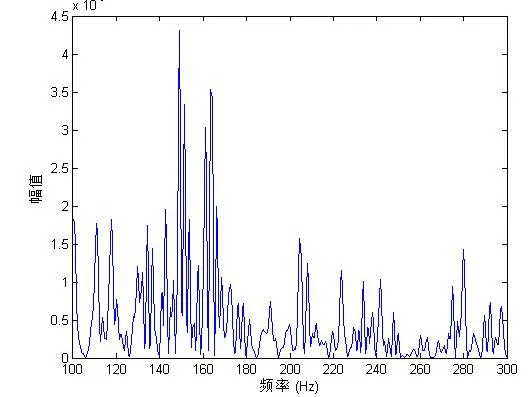
图2 频率响应

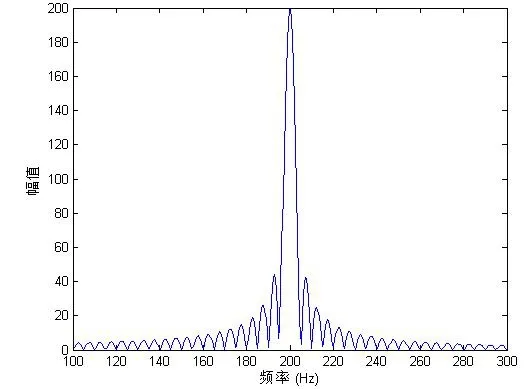
图3 发射信号频谱

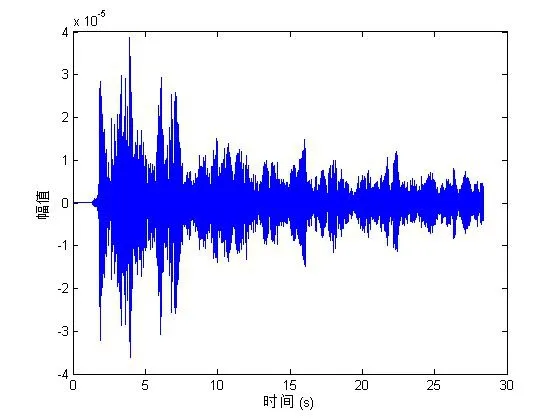
图4 混响声压

4 结束语

本文提出了一种基于简正波理论的混响声压模型，通过傅里叶变换将发射信号分解成不同频率成分，分别计算各个频率的传播衰减和传播时延，从而计算海洋声信道的频率响应，获得混响的声压信号。通过仿真验证了该方法的有效性。由于该方法将发射信号分解成不同频率分量，因而也适用于宽带信号。该方法可作为混响信号仿真的一种参考，结果用于声呐信号处理方法的评估。