n个n维向量的等价性质及应用*
2018-07-10闻道君陈义安
闻道君, 陈义安
(重庆工商大学 数学与统计学院, 重庆 400067)
0 引 言
“线性代数”是高等院校大学数学基础课程之一,而向量是“线性代数”中的一种简单的矩阵和基本运算单元。向量与向量之间的各种线性关系是理解和掌握线性方程组、线性变换和线性空间的关键,也是进一步求解线性模型的基础理论。然而,对初学者来说,向量组的线性相关和线性无关的判定、向量组与行列式、矩阵、线性方程组和矩阵的特征值之间的联系既错综复杂,又是重要学习内容而无法回避。因此,部分同学在“望题兴叹”之后得出“线性代数”太抽象和难学的结论。
另一方面,随着MOOC等优质课程资源在大学数学教学中的广泛应用,在线课程以及在线辅助学习平台的逐步建设和推进,学生能够从在线课程中免费获取优质课件和视频资源,并能从在线讨论区获得同伴的帮助,解决学习中发现的疑惑。便利的在线自助和互助学习模式提高了解决疑问时效性,在一定程度上使得教师的功能和重心转移到指导课程学习、归纳总结和组织探讨等方面。鉴于此,笔者结合多年的教学实践,从“线性代数”中的n个n维向量开始,建立一系列与之相关的等价结论,将“线性代数”课程各个章节的内容联系起来,从学习者的角度探讨和归纳这门课程的基本知识结构;最后,举例说明这些等价性质在求解研究生入学考试题和一些跨章节的综合性问题方面的应用。这些等价结论及应用是深入理解“线性代数”的前提,也是在当前混合教学模式的“碎片化”学习之后实现“线性代数”课程相关知识点“系统化”的必经之路。
1 主要定理
数域F中n个数a1,a2,…,an组成的有序数组称为数域F上的n维向量,记为
α=(a1,a2,…,an)T
也称α为列向量。同时,记向量x=(x1,x2,…,
xn)T,b=(b1,b2,…,bn)T。
定理1 设α1,α2,…,αn为n个n维列向量,记A=(α1,α2,…,αn),如果向量组α1,α2,…,αn线性无关,则下列命题等价:
(1)r(A)=r(α1,α2,…,αn)=n;
(2)|A|≠0;
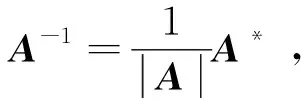
(4)A可以表示为系列初等矩阵的乘积,即A=P1P2…Ps,其中P1,P2,…,Ps为初等矩阵;
(5)Ax=b存在唯一解x=A-1b;
(6)Ax=0仅有零解;
(7)A的特征值λ≠0;
(8) 对任意n维向量β,向量组α1,α2,…,αn,β线性相关,且β可由α1,α2,…,αn进行唯一线性表示。
证明(1) 如果α1,α2,…,αn线性无关,则α1,α2,…,αn为自身的极大无关组,所含的向量个数即r(A)=r(α1,α2,…,αn)=n。
(2) 因为r(A)=n,则A中存在一个n阶非零子式,即|A|≠0。
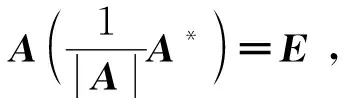
(4) 因为A可逆,结合r(A)=n可得A的行最简形为E:A≅E。由初等变换的可逆性,经过有限次初等变换E可变换为A,即
A=P1P2…Ps
其中P1,P2,…,Ps为初等矩阵。
(5) 因为初等矩阵可逆,故A可逆,即A-1存在。由Ax=b可得x=A-1Ax=A-1b,同时,利用|A|≠0和克莱默法则得Ax=b有唯一解。因此,x=A-1b是Ax=b唯一解。
(6) 因为Ax=b存在唯一解,即A-1存在。令b=0可得x=A-10=0,即x=0是Ax=0唯一零解。
(7) (反证法)假设A存在一个特征值λ=0,且Aβ=λβ=0(β≠0)。
又因为Ax=0存在唯一零解,即β=0,这与特征向量的定义矛盾,故A的特征值λ≠0。
(8) 因为任意n+1个n维向量一定线性相关,所以向量组α1,α2,…,αn,β线性相关。
另一方面,设存在实数k1,k2,…,kn使得k1α1+k2α2+…+knαn=β,即方程组AK=β,又由定理1的(1)和(6)得:
r(A)=n=r(A|β)
所以存在唯一的K=(k1,k2,…,kn)T满足ΑΚ=β,即β可由α1,α2,…,αn进行唯一线性表示。
最后,在定理1(8)中包含β=0,即
k1α1+k2α2+…+knαn=0
即方程组ΑΚ=0存在唯一零解,即ki=0。
因此,向量组α1,α2,…,αn线性无关。
定理2设α1,α2,…,αn为n个n维列向量,记A=(α1,α2,…,αn),如果向量组α1,α2,…,αn线性相关,则下列命题等价:
(1)r(A)=r(α1,α2,…,αn) (2)|A|=0; (3)A不可逆; (4)Ax=0存在非零解; (5) 如果r(A)=r(A|b) (6)A至少存在一个特征值λ=0; (7) 向量组α1,α2,…,αn中至少存在一个向量能由其余向量进行线性表示。 证明由定理1的等价性质(1)—性质(8),不难证明定理2中与之对应的系列等价性质。 例1(2012年研究生入学考试第5题)设向量组 (A)α1,α2,α3 (B)α1,α2,α4 (C)α1,α3,α4 (D)α2,α3,α4 解由定理2的性质(2)和性质(7),n个n维向量线性相关的充要条件是|α1,α2,…,αn|=0,且 则对任意的c1,c2,c3,c4,向量组α1,α3,α4必线性相关,故选(C)。 (A)a∉Ω,d∉Ω (B)a∉Ω,d∈Ω (C)a∈Ω,d∉Ω (D)a∈Ω,d∈Ω 解由定理2的性质(2)和性质(5),因为Ax=b有无穷多解的充分必要条件为r(A)=r(A|b) 令|A|=(a-1)(a-2)=0,解得a=1或a=2,即a∈Ω。同理,由r(A)=r(A|b)得d∈Ω,故选(D)。 例3设三阶矩阵A,A-E,A+3E均不可逆,计算行列式|A+2E|。 解由定理2中性质(3)和性质(6),设 Aα=λα(α≠0) 至少存在一个特征值λ1=0。因为 (A-E)α=(λ-1)α 所以λ-1是A-E的特征值,至少存在一个λ2=1。 同理,λ+3是A+3E的特征值,至少存在一个λ3=-3。因此, |A+2E| =(λ1+2)(λ2+2)(λ3+2)=-6 例4设A为三阶矩阵,Aαi=λiαi(αi≠0),i=1,2,3,且λi为3个不同的特征值。证明A可逆的充要条件是A(α1+α2),A(α2+α3),A(α3+α1)线性无关。 证明由定理1中(2)(3)和(7),A可逆的充要条件是|A|=λ1λ2λ3≠0。 因为λ1,λ2,λ3互不相同,所以特征向量α1,α2,α3线性无关,则|α1,α2,α3|≠0,且 (A(α1+α2),A(α2+α3),A(α3+α1))= (λ1α1+λ2α2,λ2α2+λ3α3,λ3α3+λ1α1)= |A(α1+α2),A(α2+α3),A(α3+α1)|≠0 即向量组A(α1+α2),A(α2+α3),A(α3+α1)线性无关。 从n个n维向量出发,利用矩阵分块的方法讨论了向量组的线性关系与行列式的值、矩阵的秩、矩阵的初等变换、线性方程组的解和矩阵的特征值等问题之间的内在联系,建立了关于n个n维向量的一系列等价性质。这些等价性质是深入理解“线性代数”课程各章节内容的关键,也是学习者建构自身知识体系的重要内容。最后,举例说明了系统掌握这些等价性结论在解决一些综合性的考研试题方面的有效性。 参考文献(References): [1] 袁晖坪,郭伟.线性代数 [M].北京:高等教育出版社,2010 YUAN H P, GUO W. Linear Algebra[M]. Beijing: Higher Education Press,2010 [2] 吴赣昌.线性代数(经管类)[M].第五版.北京:中国人民大学出版社,2017 WU G C. Linear Algebra (Economics and Management) [M].5th edt. Beijing: China Renmin University Press,2017 [3] 黄先开,曹显兵.2017年考研数学最新精选600题(经济类)[M].北京:中国人民大学出版社,2016 HUANG X K, CAO X B. The Latest600Questions Selecting for Graduate Record Examination in2017(Economics)[M].Beijing: China Renmin University Press,2016 [4] 李红婷.高师“数学教学论”课程建设的反思与重构 [J].西南师范大学学报(自然科学版),2010,35(6):196-200 LI H T. Reconsideration and Reconstruction of the Curriculum Reform of “Mathematics Pedagogy” in Normal Universities [J]. Journal of Southwest China Normal University(Natural Science Edition),2010,35(6):196-200 [5] 江蓉,王守中.矩阵的秩在线性代数中的应用及其教学方法的探讨 [J].西南师范大学学报(自然科学版),2012,37(8):175-180 JIANG R, WANG S Z. On Application of Rank of Matrix in Linear Algebra and the Methods of Teaching [J]. Journal of Southwest China Normal University(Natural Science Edition),2012,37(8):175-180 [6] 闻道君,陈义安,唐艳.高等院校经管类专业的数学教学方法研究 [J].重庆工商大学学报(自然科学版),2011,28(4):413-416 WEN D J, CHEN Y A, TANG Y. On Teaching Approach to College Mathematics for Economic and Managerial Major [J]. Journal of Chongqing Technology Business University(Natural Science Edition),2011,28(4):413-416 [7] 闻道君,唐艳,陈义安.支架式教学:一个重要极限的抽象方法 [J].重庆工商大学学报(自然科学版),2014,31(10):78-80 WEN D J, TANG Y, CHEN Y A. Support Teaching: Abstract Methods for an Important Limit [J]. Journal of Chongqing Technology and Business University(Natural Science Edition),2014,31(10):78-802 应用举例
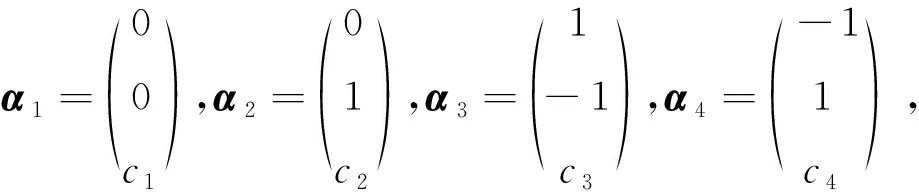
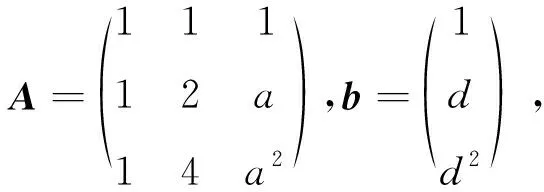
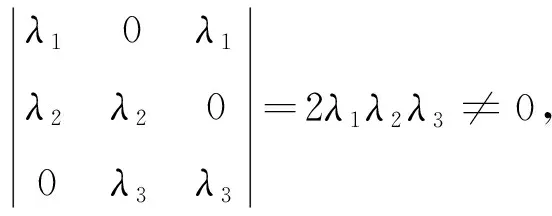
3 结束语
