给空间想象插上逻辑的翅膀——小学六年级“图形与几何”总复习教学策略

江苏南京市高淳区实验小学　赵三多

“图形与几何”领域最核心的目标是发展学生的空间想象力，其体现在空间观念与几何直观的培养中，渗透于数学学习的各个阶段。在小学六年级“图形与几何”总复习阶段，如果教师能够深入钻研教材，合理设计复习活动，帮助学生进一步建立空间观念、形成几何直观，定会在“发展空间想象力”方面取得阶段性、层次性的突破，必将促进学生形象思维能力与抽象思维能力的全面发展。

但当下“图形与几何”总复习教学中，重复学习、反复训练、题海战术等高耗低效地教学，使学生的空间想象力停滞不前，这对后续学习是极为不利的。笔者认为只有充分发挥逻辑在“图形与几何”总复习中的力量，才能有效提升复习教学效率，才能有效提高学生的空间想象力水平。

一、不忘教材“初心”，理解“逻辑”意义

2013版小学数学教材将总复习“空间与图形”领域更名为“图形与几何”，将四大板块中“图形与变换”更名为“图形的运动”。与旧版教材对比，具体内容的编排.变化较小，知识点的范围没有增减。

为什么教材要有这样的变化呢？笔者认为主要有两点原因。一是为研究内容正名，小学阶段学习的主要是欧几里得几何，以“图形与几何”命名更为准确；“图形的变换”主要研究图形的平移、旋转、翻转等运动，以“图形的运动”命名更为合理。二是以“图形与几何”命名，更准确地揭示了研究内容与研究方法；从“空间”中抽象出的是“图形”，而研究方法则是几何学。这些变化，可以明确教材编排的“初心”是注重知识与方法的统一，注重空间观念与几何直观的培养，注重学生空间想象力的提升。

教材的分块编排体现了怎样的“逻辑”意义呢？众所周知，逻辑发展大致经历了具象逻辑、抽象逻辑（形式）、对称逻辑（辩证）三大阶段。教材中“图形的认识”与“图形的测量”分别从宏观与微观层面引导学生认识图形抽象模式及元素数量特征，两者是对静态空间图形的认识，总复习时应该注重学生整体思维与抽象思维水平的提升，应该体现具象逻辑与抽象逻辑的意义。“图形的运动”是在运动变化中掌握图形“不变”的特征，“图形与位置”是从数量关系上理解图形的性质，两者是对动态空间图形的认知，总复习时应该注重学生抽象思维与辩证思维水平的提升，应该体现抽象逻辑与对称逻辑的意义。

二、捋顺知识外在的先后逻辑，将已有认知纳入结构

“图形与几何”领域总复习，要体现“复习课”教学的一般要求：一是突出查漏补缺，体现因材施教；二是突出知识梳理，沟通知识联系；三是建构知识网络，提升综合理解。同时，要体现该领域内容的特殊性和顺序性，更要关注知识与方法的统一性和延续性。

图1

如“平面图形的面积”总复习，教师通常会进行三个环节教学：回忆各图形面积计算公式、回顾公式推导过程（如图1）、习题巩固训练。笔者认为，在上述复习的基础上，还应该引导学生思考三个关键问题：为什么要按这样的先后顺序学习？理解这样的先后顺序有什么作用？能改变这样的学习顺序吗？前两个问题关注知识学习顺序及推导过程中的逻辑关系。教师借助“具象逻辑”的力量，发展学生的整体思维水平，引导学生将知识纳入到结构中。第三个问题诱发认知冲突，借助“对称逻辑”的力量，发展学生的辩证思维水平。

三、探究知识内在的关联逻辑，发挥结构的学习力量

对“图形与几何”领域的复习，不能仅停留在建立知识结构的层面，更应强调对知识结构的内化、反思与创新，实现思维内容与思维形式的统一。

如“平面图形的面积”总复习一课中，学生明确了“长方形面积公式”是其他图形面积公式推导的基础。在此基础上引导学生思考：我们所学的平面图形都可以转化为长方形并推求面积，能不能统一转化为其他图形呢？如果可以，这样的转化对我们有什么帮助呢？

学生通过探究发现：所学平面图形的面积计算都可以统一转化为梯形的面积来计算，长方形、正方形、平行四边形可以看作是上、下底相等的梯形，三角形可以看作是上底为0的梯形。这一发现对于学生操作“画面积相等的平面图形”等习题有很大的帮助。同时，充分理解知识内在的关联逻辑，可以发挥结构的学习力量，有利于学生面对认知盲点时，依赖认知结构的力量自行修复、补充和完善。

正所谓“不破不立”，学生通过对平面图形的面积进行再演绎、再归纳，借助“抽象逻辑”与“对称逻辑”的力量，进一步沟通图形之间的关系，进一步体会公式、定理的正确性、普遍性、关联性，进一步提高空间观念与几何直观的水平，提升空间想象力。

四、体会知识发生的辩证逻辑，提升元认知能力

元认知能力本质上是学生对自己认知过程的审视能力与调整能力，其发展因人而异、因学而异。总复习阶段的学习内容与学习方式的特点都决定了此阶段是小学学习中元认知能力发展的最佳时期。所以，在“图形与几何”领域的复习中，学生一定要避免“鸟笼效应”，杜绝为复习而整理的现象，要真正从提升认知水平、认知能力和元认知能力方面来思考复习。

第一，要“有广度”地复习，帮助学生建构完整的知识体系，强化“关键知识”的再学习、再思考。如“圆的周长与面积”“圆柱的表面积”等易错知识的再学习时，要引导学生审视自我学习历程，发现过程与方法上存在的问题和原因，交流改进方法与策略，这比单一纠正某个错误更有价值。

第二，要“有深度”地复习，适度延伸铺垫，为学生的后续学习“添砖加瓦”。这里的“延伸铺垫”既有知识延伸，也有学法延伸，更有情感延伸。如“角的分类”总复习环节中，引导学生“把角按大小有序排列”（如图2），并提出如下问题供学生思考：大于180度且小于360度的角叫什么角呢？有没有大于360度的角呢？当有这样的疑问时该怎么办呢？学生思考如何去获取知识，比明确“优角与劣角”的知识更重要，学生对自己学习过程与策略的思考比得到结论更有价值。

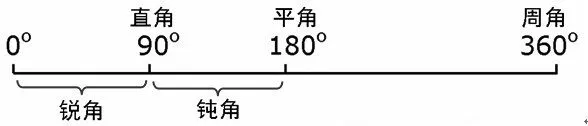
图2

教师可在“圆柱、长方体、正方体”体积公式的复习后，适时出示多种“直棱柱”思考体积计算中的规律；在“圆锥”体积公式复习后，适时出示部分“圆台”启发学生思考计算原理等。对于这些问题的思考，不强调结论的完整，强调学生主动地探究、沟通、创新，强调学生对自己学习态度、学习方式、学习能力的审视。

第三，要“有温度”地复习，彰显教师的人文关爱。例如，在关于“图形的认识”的复习时，教师通常引导学生从点、线、面、体的逻辑定义出发，进行演绎式地展开，引导学生逐步建立起完整的思维导图。教师既要通过思维导图加深学生对知识的理解，形成完整的认知结构，更要引导学生对思维导图的使用价值、使用心理体验等进行评判与反思，促进元认知能力的提升，这对于学生后续学习将大有裨益。

诚然，“图形与几何”的复习教学不争一课之功，“空间想象力”的提升也非一蹴而就。唯心中有学生，眼中有教材，手中有“课标”，脑中有“逻辑”，且行且思，坚持不懈，方可为数学思维插上飞翔的翅膀，让学生在数学知识的海洋中自由翱翔。

【参与文献】

［1］乔尚义，浅谈初中数学空间想象能力的培养［J］.教育教学论坛，2011（9）.

［2］李文革，小学数学逻辑思维能力的培养［J］.成功（教育版），2013（16）.♪