例谈几何直观在小学数学教学中的应用
2018-07-10江苏徐州经济技术开发区实验学校
江苏徐州经济技术开发区实验学校 孔 明
几何直观主要是指利用图形描述与分析问题,借助几何直观可以将抽象的数学语言与直观的图形有机地结合起来,从而使思维的本质直接展现在学生面前,帮助学生打开思维的大门,开启智慧,使学生能够轻松地获得知识与本领。那么,几何直观在小学数学教学中到底有何优势呢?笔者认为,教师可以从以下方面去尝试。
一、借助几何直观,理解抽象概念
小学生正处于形象思维向抽象思维过渡的阶段,对于数学教材中的概念来说,由于受知识水平与思维水平的限制,学生很难用数学的语言对概念进行表述,这就直接影响了学生对数学概念学习的效果。因此,教师如能根据需要把几何直观引入数学课堂,则学生更容易理解与接受。
例如,在教学《平均数》这部分内容时,为了使学生获得对平均数这个概念的深刻理解,笔者设计了一个这样的问题:老师身高175厘米,假如一条河的平均水深是140厘米,请问这条河里的水能没过老师吗?对于教师提出的问题,有学生认为不能,因为平均水深是140厘米,没有老师高;有学生认为平均水深并不是说所有的水深都是140厘米,而是有的地方可能低于140厘米,有的地方可能高于140厘米。那么,到底哪些学生的看法比较正确呢?借助几何直观的特点,笔者向学生出示了下图:

然后,笔者让学生先观察,再说说自己有什么发现。在这个直观图中,学生们可以清楚地看到老师的高度在这个平均水深140厘米的水里可能遇到的各种情况,也就是说在经过什么位置的时候水不会没过老师,什么位置的水会没过老师,这样教学,不仅解决了学生心中的疑问,而且有助于学生对平均数这个概念的真正理解。
平均数概念是一个虚拟数,比较抽象,在教学的时候,笔者主要从学生熟悉的生活情境为学生提供了一个可以尽情发表自己看法的平台,当学生对概念的理解不够透彻时,笔者又借助几何直观为学生展示了恰当的图片,这样教学,学生们的感受更深刻,学习效果更显著。
二、借助几何直观,理解算法算理
计算教学为数学教学的“重头戏”,学生出现计算错误的主要原因与学生没有真正理解算法算理有着直接关系,在传统的计算教学上,教师往往让学生死记硬背计算的公式等,而忽略学生对算法算理的直观感知,以至于学生的计算总是停留在简单地模仿或生搬硬套阶段,很难真正深入理解,针对这种情况,教师如能借助几何直观来指导学生学习,定然会使学生真正知其然而且知其所以然。
例如,在教学《有余数的除法》这部分内容时,如果教师只是让学生死记硬背有余数除法的算法算理,那么即使教师一再强调“余数一定要比除数小”,学生的感受也不一定会深刻,依然会出现在计算时余数比除数大的错误,这主要是由学生缺乏对有余数除法过程中的直观感受体验造成的。同样的教学知识,在教学时,教师如能让学生以直观动手操作的形式来摆一摆,或者分一分,那么,在这种情境中,学生对于“不能再进行平均分了”定然会有更加深刻的认识,如此教学,学生在计算时出现余数大于除数的错误自然会少很多,这就为学生计算能力的提升奠定了基础。
在这个教学案例中,笔者主要以“有余数的除法”的算法算理理解为例子,强调了借助几何直观对于学生正确理解算法算理等方面起到的促进作用,这样教学,学生们学习兴致高,学习效果好。
三、借助几何直观,学会解决问题
解决问题是小学数学教材的重要组成部分之一,虽然这些数学问题的呈现是多种多样的,有图画式、对话式、图表式、文字式等,这种多样的呈现形式为学生解决问题起到了铺路搭桥的作用。但是,随着年级的升高,纯文字表述的应用题逐渐成为解决问题的主流,这就使得问题显得枯燥、乏味、抽象,不利于学生理解,在这种教学情形下,教师如能借助几何直观让学生画一画、比一比、排一排等,那么,就可以使抽象的数学问题简单化、形象化、具体化,从而帮助学生找到解题的突破口,提升学生解决问题的能力。
例如,在教学《年,月,日》这部分内容时,在解决“6月份有30天,请问6月份里有几个星期?还剩几天?”这个数学问题之后,为了提升学生对年月日的认识程度,笔者又设计了如下问题:假如在六月份里有5个星期六与星期日,那么,6月1日是星期几?在教师问题提出以后,学生们立即提出了自己的猜想,有学生认为是星期五,有学生认为是星期一……在学生争执不下时,笔者趁机提出:“你们画一个表格不就全明白了吗?可以用自己喜欢的符号表示日期,在一个月里画满30个不就可以了,大家自己排一排,看怎样排列最适合。”在教师的提议下,学生们经过画画排排,得出了下表:
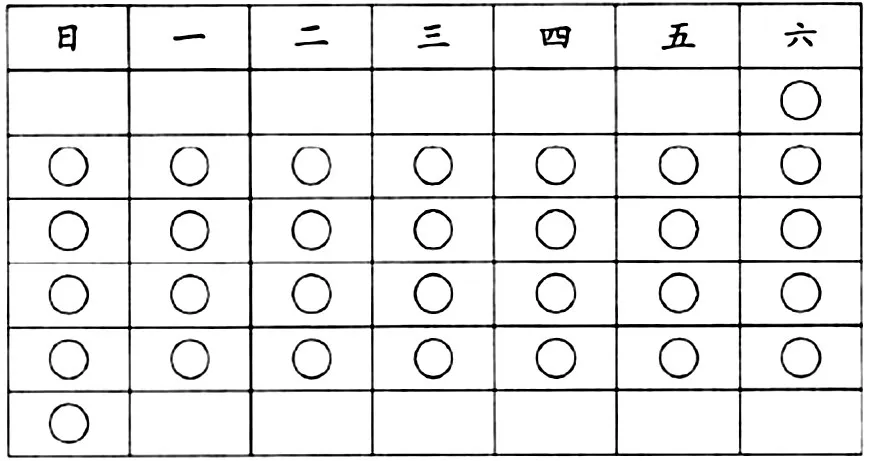
这样的结果直观清楚,学生们很容易就明白了6月1日应该是星期几,比起教师单纯用数学理论知识讲解好懂多了。
在这个教学案例中,针对学生最难把握的星期排列问题,笔者主要让学生借助几何直观的思想来排一排、画一画,这样教学,学生可以从图示中清楚地看到每一天在6月份里的排列情况,有助于学生的思维向抽象阶段过渡,从而达到帮助学生轻松解决数学问题的目的。
总之,数学是一门逻辑性、抽象性比较强的学科,不仅需要学生具有一定的抽象能力,还需要一定的几何直观能力。因此,在课堂教学中,教师要让学生在学习中感受到几何直观的优势与价值,这样一来,学生不仅学到了数学知识,而且学生的几何直观能力也得到了明显提升,从而使学生的数学学习变得更加简单、轻松。♪
