一种基于自适应同步因子的混合蛙跳算法∗

李敏楠 刘 升

1 引言

Eusuff等［1～2］于 2003 年提出了混合蛙跳算法（SFLA），该算法结合了粒子群算法和模因算法的特性，因此具有全局寻优能力强，计算速度快等优点。但算法在进行局部搜索时，每次组内迭代时个体都要重新根据初始蛙跳规则对最差个体进行更新，因此这种更新存在不确定性，导致算法在对复杂函数进行优化求解时，易出现收敛速度慢、精度低等问题。

文献［3］采用一种新的搜索策略，根据个体的差异性自主选择不同的位置更新方式，加快算法收敛速度，提高了种群的多样性。文献［4］为了加速算法收敛，避免陷入局部最优，对蛙跳更新规则进行改进，并对最差个体进行混沌扰动，结果证明有效。文献［5］基于比例系数和适应度标准差来自适应调整更新，改进了SFLA对高维问题求解的有效性。文献［6］在算法局部搜索策略中，对子群内最差个体的更新融入了服从正态分布的变异扰动，扩大了搜索空间，增加了种群的多样性。文献［7］结合贪婪算法与模拟退火算法，对算法在局部搜索时是否陷入局部最优进行判断，继而选择相应策略进行位置更新。在算法的应用研究方面，许多学者也对该算法进行了相应改进后，用于实际问题的优化当中，如云资源调度、车间布局优化以及产品装配序列等研究中，也为蛙跳算法的改进提供了诸多思路［8～12］。为了提高SFLA的收敛精度，提高算法的优化性能，本文在标准SFLA中引入同步策略因子，提出一种基于自适应同步因子的混合蛙跳算法（Adaptive Synchronized Factor Shuffled Frog Leaping Algorithm，AS_SFLA），利用同步因子改进青蛙个体的局部搜索策略，更新蛙跳规则，控制最优个体对最差个体的引导程度，提高了算法的收敛精度和优化能力。

2 标准混合蛙跳算法

标准蛙跳算法包含确定性和随机性方法。其基本思想是［1］：随机生成NI只青蛙个体组成初始种群体P=｛X1，X2，…，XNI｝，S维解空间中的第i只青蛙表示为 Xi=［xi1，xi2，…，xiS］。种群经初始化后，对种群内的青蛙个体按目标函数值大小的升序排列，并记录种群中具有最优值的个体为Xg，之后将全部个体分成m个模因组，每个模因组包含n只青蛙，满足关系N=m×n。其中：第1只蛙～第m只蛙分别分入第1模因组～第m模因组，第m+1只蛙再次归类至第1组，依次类推。设Mk为第k个模因组的个体集合，其分配规则如式（1）：

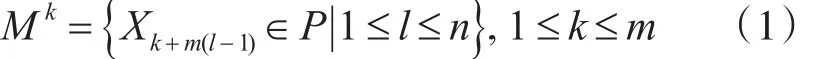
每一组中的最优个体和最差个休分别记为Xb和Xw，而整个种群的全局最优个体表示为Xg，然后对m个模因组展开局部迭代搜索，即对模因组中的最差个体Xw进行循环迭代更新操作。根据最初蛙跳规则，其更新方式为

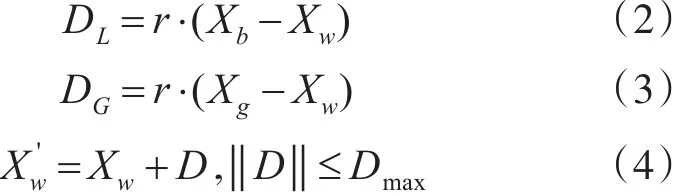
式中：r为一个随机数，且 r∈［0，1］，Dmax表示个体。

位置可以允许改变的最大值。在经过式（2）与式（4）更新后，如果产生的新个体 Xw'优于原来的个体XW，则取代相应模因组中最差个体；如果没有优化，则用全局最优个体 Xg取代 XW，按式（3）和式（4）进行局部搜索；如果仍未能优化，则进行随机更新，产生一个全新个体取代原来的最差个体，即XW。重复局部搜索过程J次，内部搜索迭代完成后，将全部模因组内的青蛙个体重新混合，重复排序过程和划分模因组，再进行局部迭代，反复进行，直到迭代次数达到最大迭代次数Gmax或满足收敛精度。全局信息交互学习并开拓局部搜索深度可以使算法能够跳出局部极值点，不断向全局最优位置靠近［13］。

3 改进的混合蛙跳算法

3.1 自适应同步因子

引入同步因子后，青蛙在进行组内搜索时，会不断地学习自身的信息来调整位置，但若同步因子固定不变，算法易陷入局部最优，影响算法效果。因此本文引入一个动态自适应的同步因子。由于组内的其他个体会随着组内迭代次数的增加不断地靠近组内具有最优位置的个体，因此个体在每次迭代中更新位置时，更新变量也不同，故利用动态的同步因子来改进蛙跳规则，可以调整个体对自身信息的学习程度，增加算法局部搜索时个体更新步长的扰动性，从而提高算法的局部搜索和全局搜索能力。综上分析，动态同步因子根据式（5）进行调整：

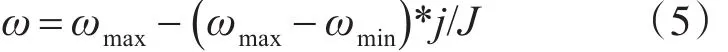
式中：ω为同步因子，ωmax，ωmin分别为同步因子的取值范围边界值，j为组内当前迭代次数，J表示组内最大迭代次数。

3.2 改进的混合蛙跳算法

3.2.1 算法描述

混合蛙跳算法（SFLA）具有寻优精度不高、算法收敛速度较慢等不足，因此在优化复杂函数问题时效果相对较差。产生这种效果是由于种群多样性随着种群的进化不断降低，从而使算法易陷入早熟收敛和局部最优。造成这一问题的原因是蛙跳算法的局部更新策略有待改进，因此本文根据上面两个公式对蛙跳规则进行改进，使算法能够跳出局部最优点，向全局最优方向搜索，引入同步因子后的局部与全局蛙跳规则如式（6）与式（7）所示：

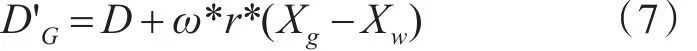
式中：D表示相对当前上次更新时的距离向量，D'L与D'G分别表示本次局部更新与全局更新时的距离向量，ω表示自适应同步因子。

3.2.2 算法流程

本文提出的AS_SFLA算法流程如下：

Step 1：参数初始化中包含全部个体NI只青蛙，个体搜索维度S，种群分组数m，每组中有青蛙个体n只，即NI=m×n。个体在改变位置时能够允许的最大变量为Dmax，组内迭代次数为J，全局最大迭代次数为Gmax。

Step 2：种群初始化。参数进行初始化设定后，随机生成NI只青蛙个体作为初始种群P=｛X1（t），…，Xi（t），…，XNI（t）｝，i=1，2，…，NI，t为迭代计数器。其中Xi（t）就作为目标函数中的自变量来计算每个青蛙个体的适应度值，即Fi（t）=F（Xi（t））；计算出每个个体的目标函数值后，对所有适应度值按数值大小的升序排列，同时以Ui（t）=｛Xi（t），Fi（t）｝的形式记录下来，并记录当前种群全局最优个体为X1（t）=U1（t）。

Step 3：种群分组。将按升序排列后的个体按式（1）分配到m个组别中M1（t），…，Mk（t），…，Mm（t），k=1，2，…，m，同时也记录下每个组别中的最优青蛙与最差青蛙，即Xbk（t）和Xwk（t）。

Step 4：组内迭代搜索。对当前种群的每一组进行组内迭代搜索，对当前组别中的最差个体Xkw（t）展开局部搜索。其更新原理仍同基本蛙跳算法，但其更新方式则是按照式（5）、式（6）与式（7）。若此更新后，结果仍未优化，则随机产生一个全新的个体作为当前组内最差个体，计算目标函数值；重新上述局部搜索次数J次，最后可以得到一个进化后的种群分组M1（t）'，M2（t）'，…，Mm（t）'。

Step 5：个体重新混合。将进化后的所有分组中的青蛙个体重新混合。重新计算当前种群个体的目标函数值，并再次按升序重新排列，记录更新后的种群最优个体为Xg（t+1）。

Step 6：算法终止判定。当迭代计数器t=t+1＜J时，跳转至Step 3；否则，输出当前最优青蛙个体。

4 仿真实验

4.1 Benchmark函数

为了验证AS_SFLA的性能，文中应用SFLA和AS_SFLA分别对所选测试函数进行优化测试，另外利用文献［14］中的数据在9个函数中选取了其中的5个函数对SFLA、ISFLA1［14］和 AS_SFLA 进行了数据比较。测试平台为Matlab R2014a和Windows7，处理器为 Intel Core i5，机器主频 3.00GHz，内存4.00GB。本文选择了9个Benchmark函数进行仿真实验，其中包括3个单峰函数和5个多峰函数，最后测试了一个二维函数。具体函数如下：

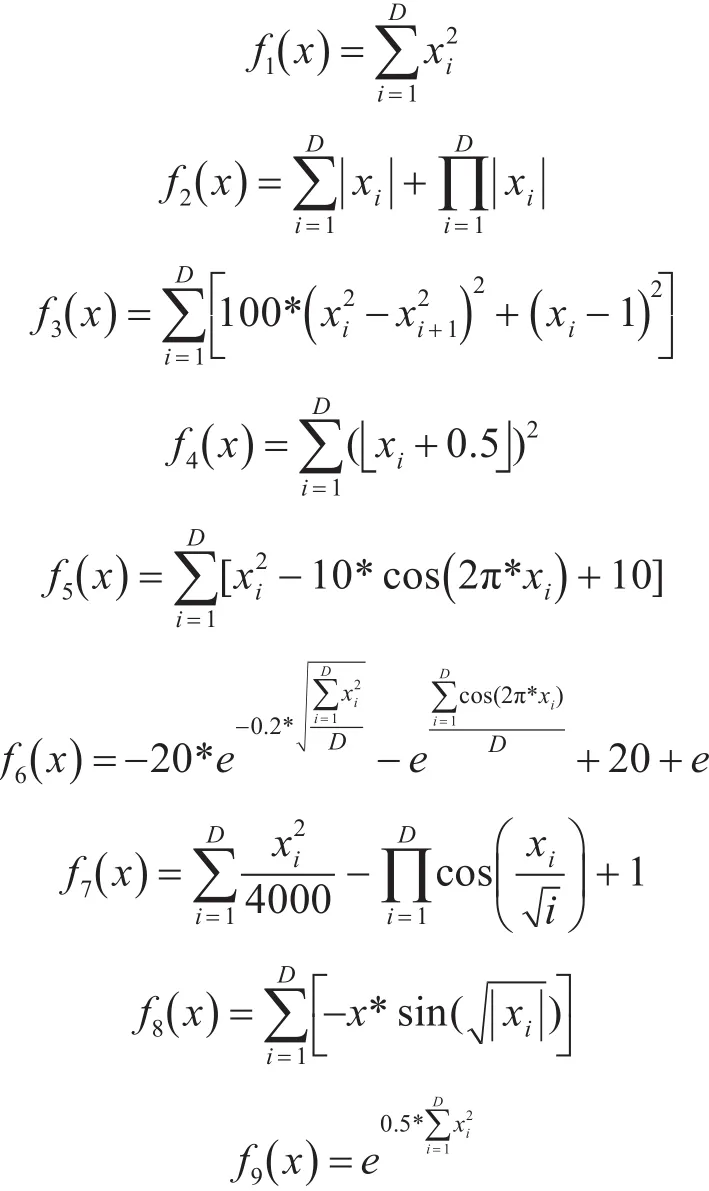
4.2 实验结果与分析

4.2.1 参数设置

本文采用SFLA和AS_SFLA进行对比，为了提高实验的可比性和准确性，设置相同参数，具体如下：青蛙总数NI=450只，模因分组数m=30，每组包含青蛙个体n=15只，组内迭代次数J=30次，全局总迭代次数Gmax=1000次，个体维度S=15，同步因子上下限分别取2.5和1，即ωmax=2.5，ωmin=1。

4.2.2 结果分析

将重复运行30次所得的结果按照函数测试Best值、Worst值与Mean值来检测算法性能，从测试结果表1与收敛曲线图1～图9中得知AS_SFLA的收敛速度更快，对于前3个单峰函数，AS_SFLA比基本蛙跳算法更接近最优值，并且在收敛精度上有很大辐度的提高。在另外5个多峰函数和一个二维函数的测试结果中，AS_SFLA也体现了较好的收敛性和较强的寻优能力，相比标准混合蛙跳算法，本文提出的算法在迭代过程中，随着同步因子不断提高，能够更加快速地收敛从而找到全局最优解，因此较基本算法已有了较大程度的改进。

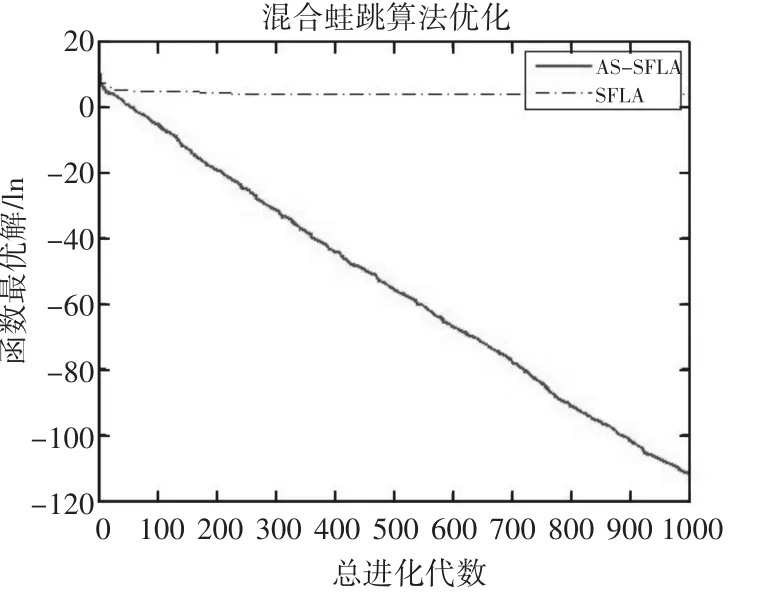
图1 不同算法在函数f1（x）下的收敛曲线（ln）

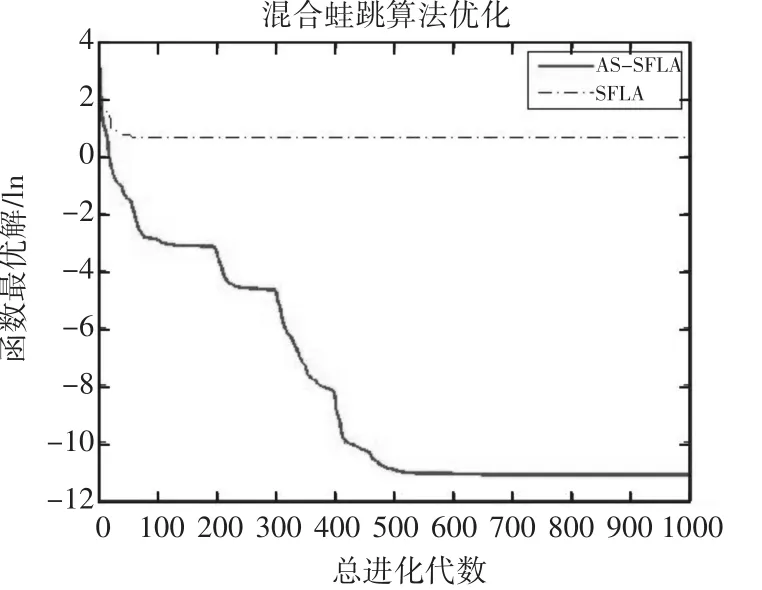
图2 不同算法在函数f2（x）下的收敛曲线（ln）

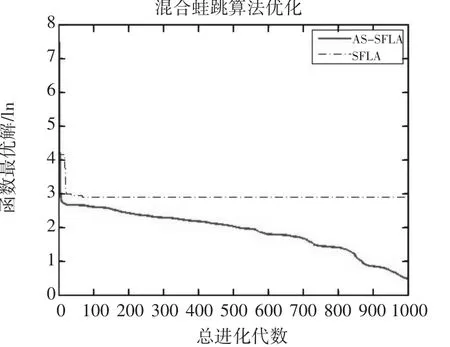
图3 不同算法在函数f3（x）下的收敛曲线（ln）

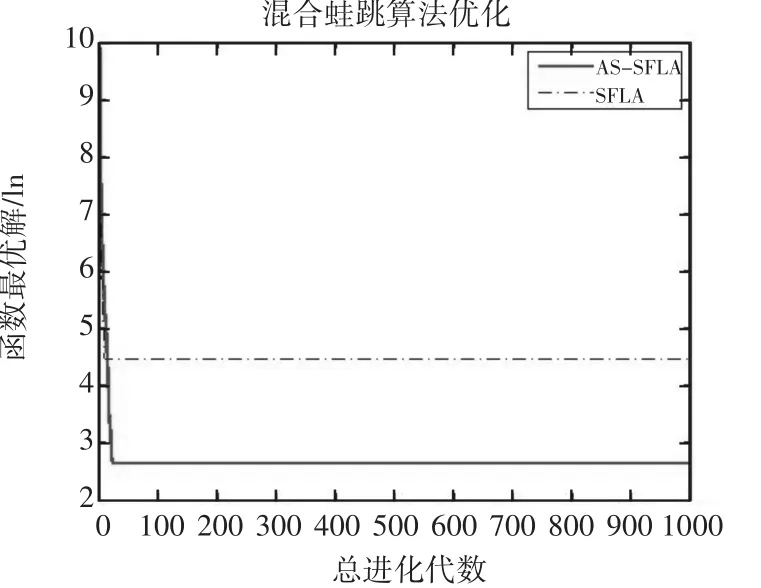
图4 不同算法在函数f4（x）下的曲线（ln）

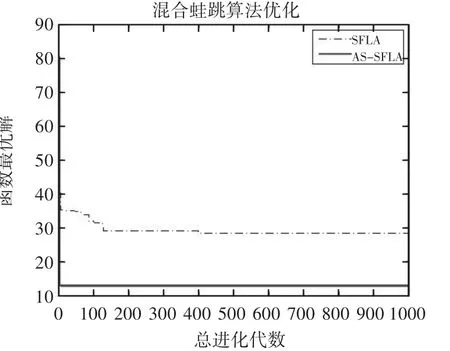
图5 不同算法在函数f5（x）下的收敛曲线

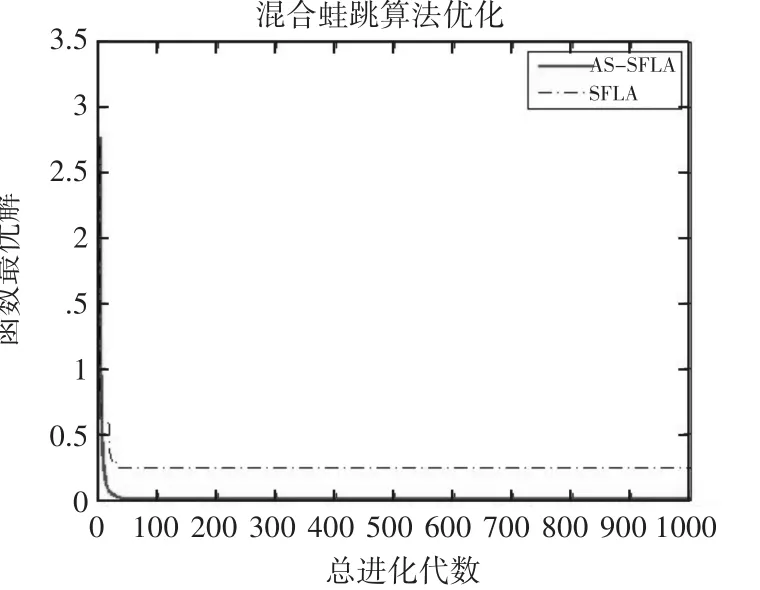
图6 不同算法在函数f6（x）下的收敛曲线

图7 不同算法在函数f7（x）下的收敛曲线

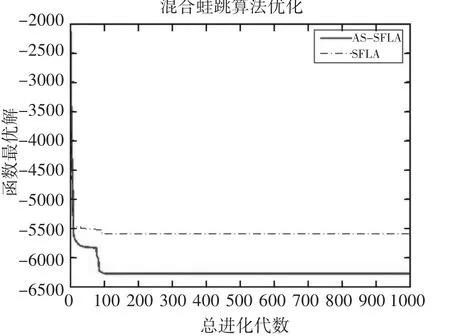
图8 不同算法在函数f8（x）下的收敛曲线

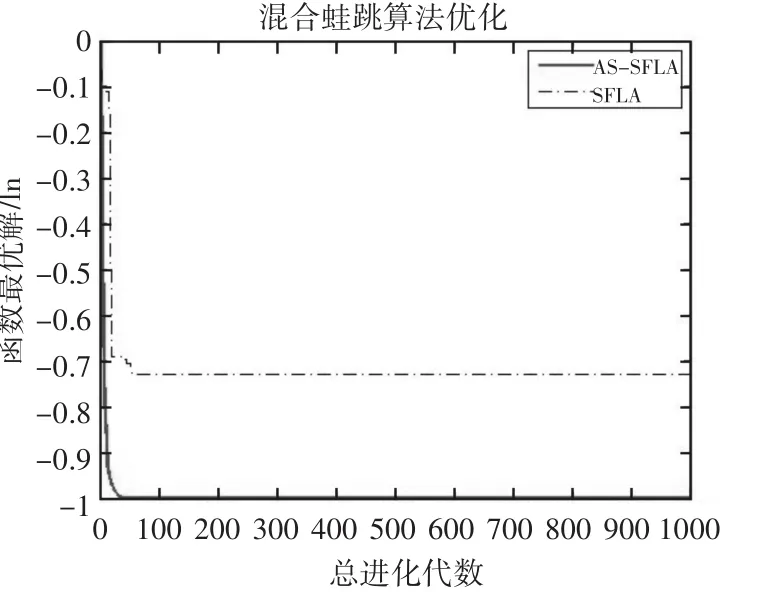
图9 不同算法在函数f9（x）下的收敛曲线

表1 不同算法在9个测试函数中的寻优结果

对于Sphere函数，AS_SFLA采用本文所用参数可以使最优解的收敛精度达到10-49量级，对于Schwefel与Ackley函数，AS_SFLA的收敛精度也达到了10-10量级，较基本SFLA有所改进。

为了进一步证明AS_SFLA的有效性，本文采用文献［14］中的数据以及参数，即：青蛙总数NI=200只，模因分组数m=20，每组包含青蛙个体n=10只，组内迭代次数J=10次，全局总迭代次数Gmax=500次，个体维度S=30，同步因子上下限分别取2.5和 2，即 ωmax=2.5，ωmin=2。 将 SFLA、ISFLA1［14］和AS_SFLA进行了5个Benchmark函数的实验，并重复运行30次后，对相关数据进行比较，具体数据如表2所示。

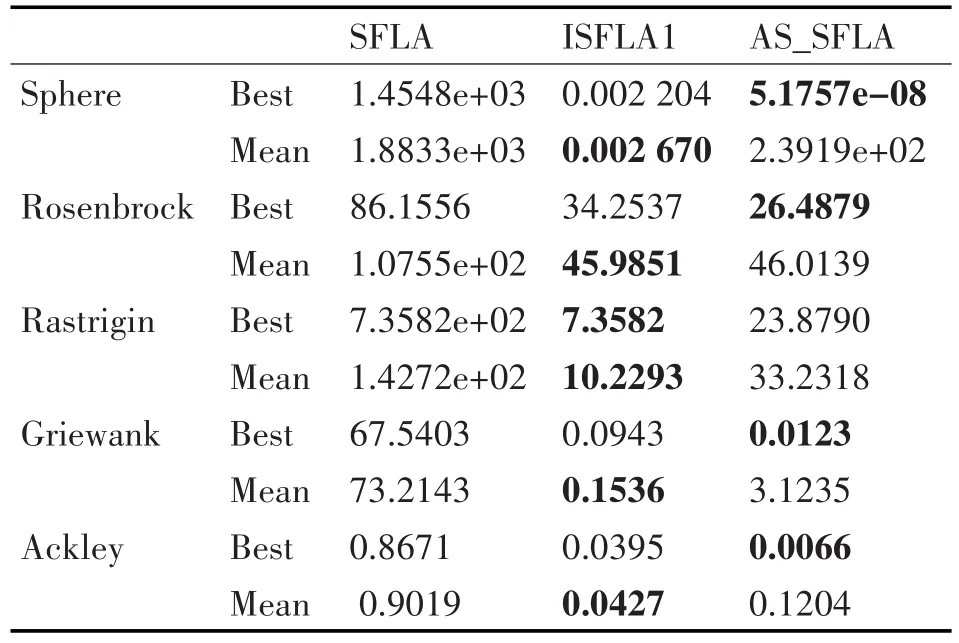
表2 SFLA，AS_SFLA和ISFLA1的5个测试函数实验数据

由表2可知，在采用了文献［14］中的建议参数后，本文提出的AS_SFLA寻优结果和收敛性依然要优于基本算法，同时经过两种算法与ISFLA1的相应数据进行对比后，AS_SFLA在Sphere函数、Rosenbrock函数、Griewank函数及Ackley函数中的最优值都要优于ISFLA1，其中对Sphere函数的测试求解精度也已达10-8。

5 结语

混合蛙跳算法基于群体协同搜索，具有一定的全局搜索能力。本文借鉴改进粒子群算法［15］的思想，在基本算法中引入自适应同步因子，更新局部搜索时的蛙跳规则，以促进算法的局部搜索深度，通过对9个基准测试函数进行仿真试验，证明了算法具有很好的收敛精度和寻优结果，对高维复杂函数能够进行有效优化，体现了算法的优越性。本文由于无文献［14］中的代码，没有对其进行收敛曲线的对比，并且该算法在前期迭代时获得的函数值较大，影响了算法的稳定性，如何能够对这个问题加以修正和改进将是下一步的研究工作。

［1］Eusuff M M，Lansey K E.Optimization of water distribution network design using the shuffled frog leaping algorithm［J］.J of Water Resources Planning and Management，2003，129（3）：210-225.

［2］Moscato P.On evolution，search，optimization，genetic algorithms and martial arts：Towards memetic algorithms［R］.Caltech Concurrent Computation Program Report 826，California Institute of Technology，1989：16-20.

［3］赵芳，张桂珠.基于新搜索策略的混合蛙跳算法［J］.计算机应用与软件，2015，32（8）：224-228.

ZHAO Fang，ZHANG Guizhu.Shuffled Frog Leaping Algorithm Based on New Search Strategy［J］.Computer Applications and Software，2015，32（8）：224-228.

［4］张沫.改进混合蛙跳算法的云计算资源调度［J］.计算机应用与软件，2015，32（4）：330-333.

ZHANG Mo.Resource Scheduling in Cloud Computaing Environment Based Shuffled Frog Leaping Algorithm［J］.Computer Applications and Software，2015，32（4）：330-333.

［5］肖莹莹，林廷宇，李伯虎，等.混合蛙跳算法自适应参数调整改进策略［J］.系统工程与电子技术，2016，38（8）：1939-1949.

XIAO Yingying，LIN Tingyu，LI Bohu，et al.Improvement strategy of adaptive patameter adjustment for shuffled frog leaping algorithm［J］.Systerms Engineering and Electronics，2016，38（8）：1939-1949.

［6］张明明，戴月明，吴定会.正态变异优胜劣汰的混合蛙跳算法［J］.计算机应用，2016，36（6）：1583-1587.

ZHANG Mingming，DAI Yueming，WU Dinghui.Novel survial of the fittest shuffled frog leaping algorithm with normal mutation［J］.Journal of Computer Applications，2016，36（6）：1583-1587.

［7］李俊.混合蛙跳算法改进及其对旅行商问题的求解［J］.软件导刊，2016，15（10）：41-43.

LI Jun.Improved shuffled frog leaping algorithm and the solution of traveling salesman problem ［J］.Software Guide，2016，15（10）：41-43.

［8］韩炜，崔喆，顾幸生.基于新型蛙跳算法的带阻塞流水线调度问题［J］.华东理工大学学报（自然科学版），2014，40（1）：86-90.

HAN Wei，CUI Zhe，GU Xingsheng.Blocking Flow Shop Based on a New Frog Leaping Algorithm［J］.Journal of East China University of Science and Technology（Natural Science Edition，2014，40（1）：86-90.

［9］王松，孙振忠，郭建文，等.基于混合蛙跳算法的复杂产品装配序列规划［J］.计算机集成制造系统，2014，20（12）：2991-2999.

WANG Song，SUN Zhenzhong，GUO Jianwen，et al.Assembly sequence planning based on shuffle frog leaping algorithm［J］.Computer Integrated Manufacturing Systems，2014，20（12）：2991-2999.

［10］刘琼，许金辉，张超勇.基于改进蛙跳算法的鲁棒性车间布局［J］.计算机集成制造系统，2014，20（8）：1879-1886.

LIU Qiong，XU Jinhui，ZHANG Chaoyong.Robust layout of floor shop based on improved shuffle frog leaping algorithm［J］.Computer Integrated Manufacturing Systems，2014，20（8）：1879-1886.

［11］张恒巍，卫波，王晋东，等.基于分布估计蛙跳算法的云资源调度方法［J］.计算机应用研究，2014，31（11）：3225-3228，3233.

ZHANG Hengwei，WEI Bo，WANG Jindong，et al.Cloud resource scheduling method based on estimation of distribution shuffled frog leaping algorithm［J］.Application Research of Computers，2014，31（11）：3225-3228，3233.

［12］王丽萍，孙平，蒋志强，等.基于并行云变异蛙跳算法的梯级水库优化调度研究［J］.系统工程理论与实践，2015，35（3）：790-798.

WANG Liping，SUN Ping，JIANG Zhiqiang，et al.Study on cascade reservoirs optimal operation based on parallel normal cloud mutation shuffled frog leaping algorithm［J］.Systems Engineering-Theory&Practice，2015，35（3）：790-798.

［13］Rahimi-Vahed A，Mirzaei A H.A hybrid multi-objective shuffled frog-leaping algorithm for a mixed model assembly line sequencing problem［J］.Computers and Industrial Engineering，2007，53（4）：642-666.

［14］刘悦婷，赵小强.一种自适应惯性权重的混合蛙跳算法［J］.计算机工程，2012，38（12）：132-135.

LIU Yueting，ZHAOXiaoqiang.Adaptive Inertia Weight Shuffled Frog Leaping Algorithm［J］.Computer Engineering，2012，38（12）：132-135.

［15］邵明臣，彭业飞，张维继，等.粒子群算法惯性权重的自适应改进与研究［J］.电脑知识与技术（网络版），2016，16（2）：196-199.

SHAOMingchen，PENGYefei，ZHANGWeiji，et al.Particle Swarm Optimization Inertia Weight Adaptive Improve And Research［J］.Computer Knowledge and Technology，2016，16（2）：196-199.