改进型细菌觅食算法求解FJSP问题∗

王新刚 衣鹏飞

1 引言

车间作业调度问题（Job-shop Scheduling Problem，JSP）一般可以描述为优化作业的加工顺序，然后使生产资源得到优化配置的过程，是典型的NP-hard问题［1］。柔性作业车间调度问题（Flexible Job-shop Scheduling Problem，FJSP）是JSP 的扩展，其除了考虑待加工工序外，还允许一个工序可以在有能力加工的多台机器中选择，提高了资源柔性，减少了资源约束，扩大了解的范围，FJSP成为比JSP更加复杂的组合优化问题［2］。由于柔性作业车间更加符合实际的生产环境，因此研究FJSP具有重要的理论意义和实际价值。

在FJSP作业中，求解过程中要经过大规模的可行性检验以保证解的可行性，直接影响算法的效率和应用性能，近年来，国内外很多学者利用多种智能优化算法对FJSP进行优化求解。G.Moslehi将改进的粒子群优化算法用于求解具有柔性特征的多目标作业车间调度问题。G Waligora等将模拟退火算法用于求解多目标的调度问题中，取得了不错的效果［3］。赵琴研究了排队论在车间调度中的应用，并给出了详细的理论依据和分析［4］。刘红军等提出了一种新型的优化遗传算法，该算法将模拟退火策略和禁忌搜索的思想融入到遗传算法中提出了模拟退火交叉机制和禁忌搜索变异机制，适合于求解车间调度问题［5］。

BFO算法是由Passino提出的模拟大肠杆菌觅食行为的新的进化计算技术［6］。本文提出一种改进的BFO算法，重点对趋化操作的运动步长以及翻转方向进行了改进，设计了自适应步长在三种情况下的变化值，并加强全局最优位置与个体最优位置在翻转方向上的引导，避免算法早熟现象的发生。将IBFO算法运用到解决FJSP问题中进行仿真试验。通过与标准细菌觅食算法和改进遗传算法（Improved Genetic Algorithm，IGA）在柔性车间调度应用中的计算结果进行对比分析，验证了算法的进步性。

2 FJSP问题描述

FJSP问题是一种特殊的作业车间调度问题，相对于传统车间调度问题，待加工工件的每一道工序都在可选择的一台或多台机器上加工，不再有机器约束的局限。

假设加工车间内有 J=(J1,J2,…Ji,Jn)个工件和M=(M1,M2,…Mi,Mn)台机器，每个工件有多道工序，其中Oij表示Ji工件对应的第j道工序。根据机器的占有情况，FJSP的调度方法有两种，分别为完全柔性作业车间调度和路径柔性作业车间调度。若各工件的每道工序选择只能选择机器集中的部分机器进行加工，则称之为部分路径柔性车间调度；若各工件的每道工序通过所有机器完成加工，则称之为完全路径柔性车间调度。两种调度情况分别如表1、表2所示，其中数字表示工序Oij在机器Mi上的加工时间，“—”表示工序Oij不能在机器Mi上加工。以工件J1为例，该工件的加工工序为（O11，O12，O13），在完全柔性调度中，J1的三个工序均可以在4台机器上加工，其中第一个工序的加工时间分别为：1，3，4，6；而在部分柔性调度中，该工序只能在M1和M2两台机器上加工，加工时间为3，6。所有机器可以加工任意工件的所有工序并不符合实际操作，相对而言，部分柔性调度方式更适合实际的加工系统。

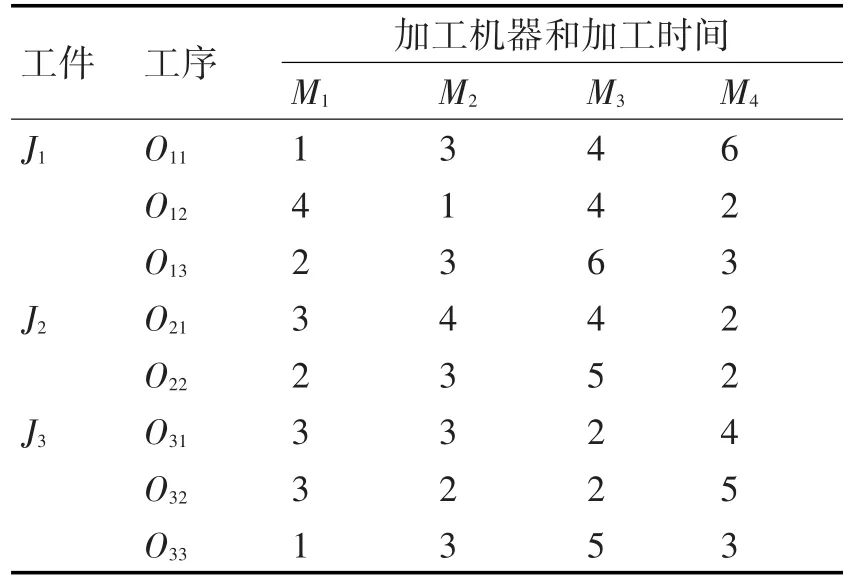
表1 完全柔性调度

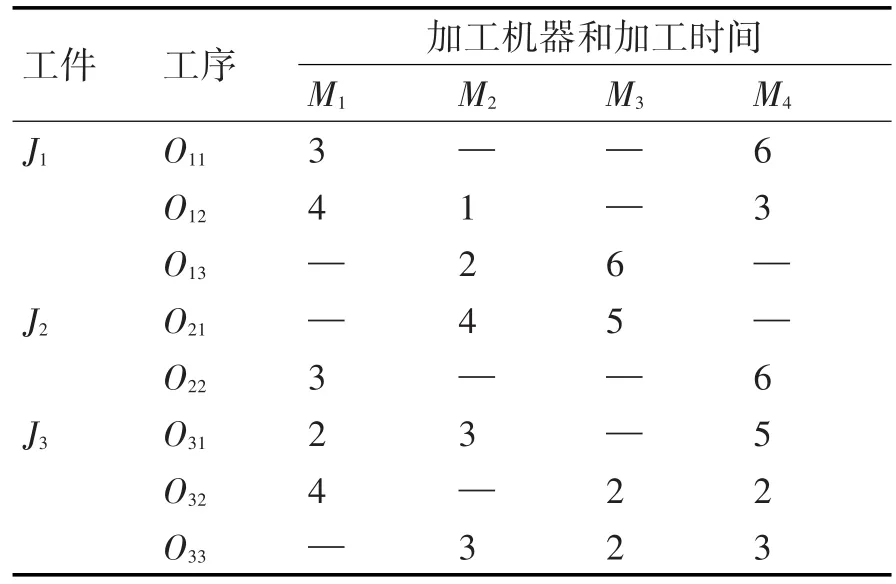
表2 部分柔性调度

3 FJSP问题的优化模型

将总任务的最大完成时间作为优化目标，设定目标函数如下：

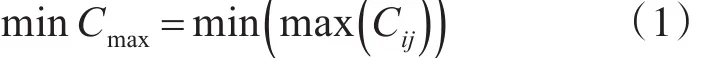
Cmax为调度任务的最大完成时间，Cij为工序Oij的完工时间。以下为优化目标的约束条件：

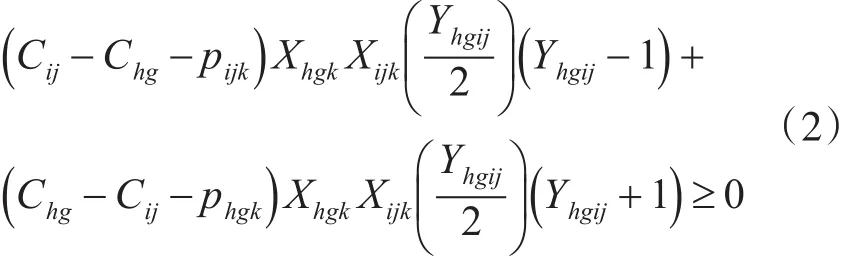
式（3）限定两个工件不能同时在同台机器上加工。其中，pijk为工序Oij在机器k上加工所需要的时间，Xijk为工序分配机器的决策变量。

Yhgij为决定工序先后顺序的决策变量。

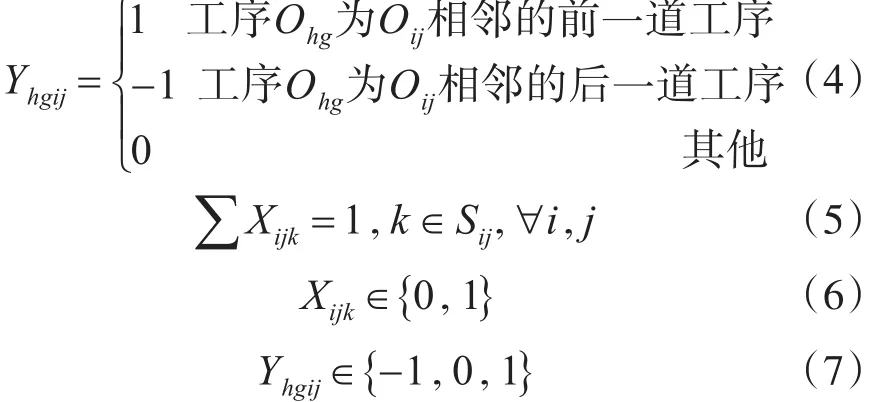
式（4）限定一道工序只能在一台机器上完成。式（5）、（6）限定决策变量的取值范围。

4 BFO算法简介

BFO算法是从生物的觅食行为中抽象出来的算法，首先确定初始解群体，通过适应度函数判断个体和群体位置的优劣，迭代运算直到达到收敛条件，算法停止。将细菌的觅食过程描述为趋向性、复制和迁移3个操作过程［7］。

趋化操作过程指细菌在解空间域内按照一定的规则进行搜索，并依据适应度进行寻找和调整行进方向的过程。趋化行为包括翻转和游动两个过程。翻转指细菌在原地随机选择一个前进方向的行为；游动指细菌沿着翻转方向或者上一次的运动方向前进，直到当前适应值低于前一步适应值，或者达到游动步数阈值。通过多次翻转和游动，细菌向目标解方向游动，最终寻找到最优解。趋化操作主要是在局部搜索最优解的过程，是算法的核心操作，决定着整个算法的寻优精度［8］。

设菌群规模是 S，用 D 维向量 Pi=（Pi1，Pi2，…，PiD）表示第i个细菌的信息，细菌i每一步趋化操作后的位置更新公式为

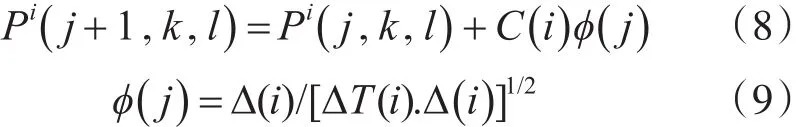
其中：表示细菌i在第j次趋化操作第k次复制操作第l次迁徙操作后的位置，即细菌i在搜索空间中的一个候选解。C（i）为细菌i游动的单位步长；Δ(i)为［-1，1］的为细菌i翻转后选择的一个随机角度矢量，φ()j为Δ(i)的标准化函数。

复制操作：当细菌完成设定的趋向性次数，后，细菌将进行分裂，这个操作主要模拟了细菌个体优胜劣汰的繁殖过程。设细菌种群大小为N，Fi（j，k，l）为个体i的适应度值，先对整个种群的适应度进行降序排列，适应度值较大的前N/2个个体保留下来，并进行无差异性分裂为二，后面的适应度较低的2/N个个体被淘汰掉，这样一次复制操作完成后，保证了细菌种群大小不变［9］。

迁移操作：为了提高算法的全局搜索能力，当一个问题的解空间存在多个极值点时，由于细菌的群聚性，算法容易陷入局部极值。这个过程是用新的个体来代替原有的个体，不同于复制操作，迁移操作是按照一定的概率p而发生的，当某个细菌符合迁移的条件时，该细菌将被随机分配到解空间中去［10］。

5 趋化操作的改进

5.1 细菌趋化步长的改进

传统算法中采用固定趋化步长，而BFO算法是一个动态寻优过程，每进行一次趋向操作，细菌的活性就会有一定比例的下降。步长越大越有可能会错过最优解，步长过小反而会过早陷入局部最优。随着趋化次数的增加，步长应该做出合适的调整，才能保持算法的搜索效率［11］。

将细菌趋化步长进行自适应改进：细菌i所在区域的拥挤度，由搜索区间内的个体数量和搜索区间长度决定，crowd=n/len；Δtj=cs(i)(j-1,k,l)-cs(i)(j,k,l)表示细菌i第j次趋化，第k次复制，第l次迁移的适应值与第j-1次趋化，第k次复制，第l次迁移的适应值之间的差值，步长共分三次变化，搜索前期处于全局寻优阶段，周围细菌数量稀少时，说明在一定范围内营养不够充分，将趋化补偿设置为较大值，有利于全局寻优，当寻找到拥挤度大的范围，则进入局部寻优状态，将步长设小，以免错过最优解。

当拥挤程度过大并且个体适应值的增长率逐渐变小时，将步长慢慢调大，以免陷入局部寻优。计算方法如下：

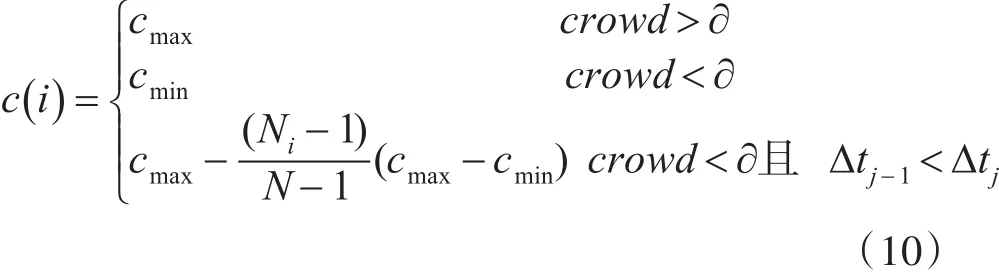
其中，Ni表示当前已经执行的趋化次数，N表示趋化总次数，cmax表示最大趋化步长，cmin分别表示最小趋化步长，∂为预设定阈值。

5.2 翻转方向的改进

在趋化过程中，记录个体的最优位置即个体趋化过程中适应值最高的位置，以及种群最优位置，即适应度最高的个体所在的位置。一般认为种群最优个体周围的环境营养更丰富，在标准细菌算法的翻转操作中，细菌的翻转方向过于随机，无法体现细菌群体在实际环境中的相互影响，因此本文提出通过两个因子来引导细菌个体的翻转方向：个体最优位置Pibest和种群最优位置Pgbest，细菌i向种群最优个体学习到的翻转方向为

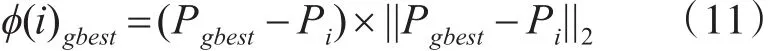
细菌i自身经过的最优位置对其引导的翻转方向为

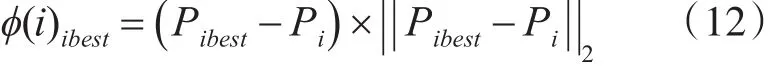
结合两个方向因子的引导，细菌i在第j次趋化操作后的翻转方向为

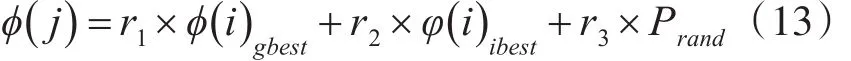
Pi表示细菌当前所在位置，Prand表示随机方向向量，r1+r2+r3=1。

6 仿真试验

6.1 算法性能分析

为了验证改进BFOA算法的有效性，本文对FJSP的标准算例Kacem的5个标准问题和Benchmark的5个经典问题进行了试验，并与标准BFOA算法和改进遗传算法（IGA）的试验结果进行了对比。本文的仿真实验环境：硬件，Intel（R）Core（TM）i5-34700 3.20GHz双核CPU，4.00GB内存；软件，操作系统为Windows 7，编程平台为Matlab。

本文通过多次试验取得的最优参数值为：细菌规模S=100，趋化次数NC=150，复制次数Nre=10和迁移／驱散次数Ned=16，趋化步长初始值设为0.15；遗传算法参数设置为：交叉概率0.9，变异概率0.1。算法对每一个算例均独立运行10次，计算结果见表3，cmax为多次实验得到的最优值，Ave（c）为平均值。

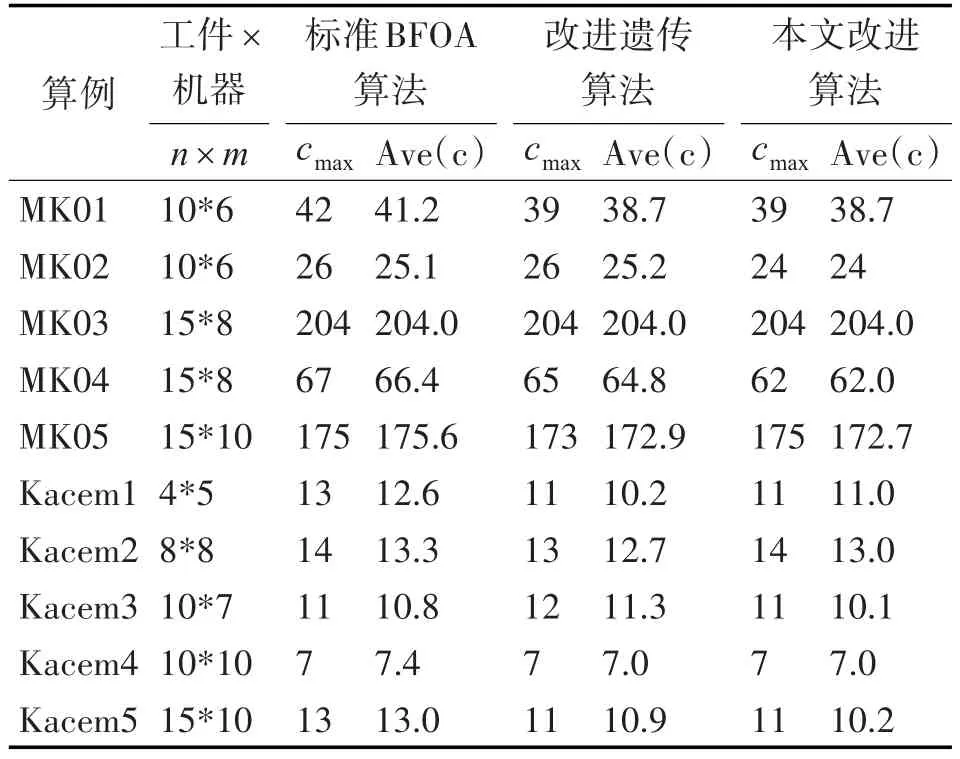
表3 算例实验结果

从表中可以看出，使用本文算法得到的最优解，除了算例MK05外，其余算例所得到的目标函数值均优于或等于另外两种算法，对于MK05这种大规模调度问题，虽然未找到最优解，但是平均解的值小于前两种算法，对于大规摸调度问题Kacem4和Kacem5，算法同样取的了比较理想的效果。因此，本文算法求解性能优于其他两种算法，虽然对于大柜摸调度问题上表现有些不稳定，但正确率还是比其他算法高一些。

6.2 实例验证

采用表中第一个Benchmark算例MK01进行验证，机器数为6台，工件数为10台，分别使用三种算法求解，对于该算例，在迭代次数200内，改进算法和IGA算法都能搜索到最优解38，而对与标准BFOA算法搜索到的解为41，图1为三种算法的收敛曲线，从图中可以看出，虽然前两种算法都能得到最优解，但IGA算法的收敛速度明显比改进算法的速度慢，改进算法在迭代30次后就找到了最优解，而IGA算法在迭代70次后才得到最优解，因此本文算法可以快速寻到最优解。图2为本文算法的甘特图，用来表示在收敛过程中算法所得到的调度方案，Y轴为机器编号，X轴为执行时间，小矩形中的数字表示“工件号-工序号”。

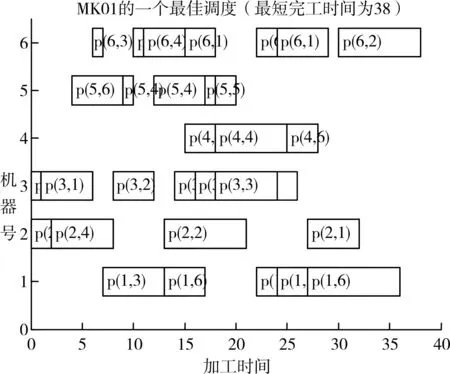
图2 MK01调度甘特图

7 结语

BFO算法是一种新兴的优化算法，然而原始的算法由于缺乏灵活性使得收敛速度慢、寻优准确率不高。本文通过深入分析细菌觅食的特性，阅读了大量相关文献，结合多方面研究，对细菌觅食算法进行了改进，并将其应用到FJSP中寻找最优解的问题上。与传统算法相比，本文方法寻优能力更加准确。与改进遗传算法相比，改进的方法减少了迭代次数，大大缩短了求解时间。但是鉴于BFO算法的程序运行略慢，参数众多，目前研究重点主要放在单目标优化上，对于求解组合优化问题上需要加强研究。

［1］崔静静，孙延明，车兰秀，等.改进细菌觅食算法求解车间调度问题［J］.计算机应用与研究，2011，28（9）：3324-3326.

CUIJingjing，SUNYanming，CHELanxiu，et al.The modified bacterial foraging algorithm shop scheduling problem［J］.Computer Application Research，2011，28（9）：3324-3326.

［2］金花，宁涛，刘芳.改进细菌觅食算法求解多目标FJSP问题［J］.化工自动化及仪表，2015，42（6）：665-668.

JINHua，NINGTao，LIUFang，et al.The modified bacterial foraging algorithm to solve multi-objective FJSP problem［J］.Chemical Industry Automation and Instrumentation，2015，42（6）：665-668.

［3］G.Waligora.Simulated Annealing and Tabu Search for Discrete-Continuous Project Scheduling with discounted Cash Flows［J］.RAIRO-Operations Research，2014，38（6）：21-25.

［4］赵琴.排队论在在车间调度中的应用［D］.兰州：兰州理工大学，2013.

ZHAO Qin.Queuing theory in the application in the shop scheduling［D］.Lanzhou：Lanzhou University of Technology，2013.

［5］刘红军，赵帅.一种基于混合遗传算法的车间生产调度的研究［J］.制造业自动化，2011，33（6）：33-35.

LIU Hongjun，ZHAO Shuai.A hybrid genetic algorithm based on the research of workshop production scheduling［J］.Manufacturing Automation，2011，33（6）：33-35.

［6］G.Moslehi，M.Mahnam.A Pareto approach to multi-objective flexible job-shop scheduling problem using particle swarm optimization and local search［J］.International Journal of Production Economics，2011，39（8）：14-22.

［7］杨大炼，李学军，蒋玲莉，等.一种细菌觅食算法的改进与应用［J］.计算机工程与应用，2012，48（13）：31-35；

YANGDalian，LIXuejun，JIANGLingli，et al.A bacterial foraging algorithm improvement and application［J］.Computer Engineering and Application，2012，48（13）：31-35.

［8］Shiv P，Deo PV.A Hybrid GABFO Scheduling for Optimal Makespan in Computational Grid［J］.International Journal of Applied Evolutionary Computation，2014，5（3）：57-83.

［9］张利平.作业车间预反应式动态调度理论与方法研究［D］.武汉：华中科技大学，2013.

ZHANF Liping.Job-shop pre reactive dynamic scheduling theory and method research［D］.Wuhan：Huazhong University of Science and Technology，2013.

［10］姜建国，周佳薇，郑迎春，等.一种双菌群细菌觅食优化算法［J］.深圳大学学报，2014，31（1）：43-51.

JIANG Jianguo，ZHOU Jiawei，DENG Yingchun，et al.A double bacteria bacterial foraging optimization algorithm［J］.Journal of Shenzhen University，2014，31（1）：43-51.

［11］HMIDA A B，HAOUARI M，HUGUET M J，et al.Discrepancy search for the flexible job shop scheduling problem［J］.Computers and Operations Research，2010，37（12）：2192-2201.