一维非线性系统FPK方程的TVD Runge-KuttaWENO型差分解

王文杰 封建湖

(长安大学理学院数学系, 西安 710064)

引言

FPK方程于20世纪初由Fokker与Planck首先提出,并应用于研究量子物理问题.20世纪30年代初Kolmogorov将它一般化与抽象化.不久,Andronov等将它应用于研究一般动态系统.50年代Stratonovich将它应用于研究电子工程问题.50年代末Chuang与Kazda将它应用于研究非线性控制系统.60年代初Ariaratnam、Lyon、Smith、Caughey与Dienes、Crandall等将它应用于研究非线性随机振动问题.

利用转移概率密度求解系统的各种响应统计量,可对该系统的响应和可靠性等做定性分析.但是,目前只对一些特殊的非线性随机动力系统,才能得到其FPK方程的精确解[1-3].基于此,许多学者致力于FPK方程数值解法的研究,其中有代表性的主要有：有限元法,有限差分法, 路径积分法,等价线性化方法,高斯闭合法,摄动法,Gram-Charlier展开法,等价非线性系统法,随机平均法等.

但这些方法各有其局限性,例如：有限元法一般都很大,而且计算得到的尾部概率密度不太准确.等价线性化方法和高斯闭合法对强非线性[4-8]或具有随机参激的系统就不适用,因为此时系统响应的稳态概率密度往往是非高斯型的.摄动法只适用于弱非线性系统.Gram-Charlier展开法可能导致概率密度为负值的情形.等价非线性系统法要求两个非线性系统性质很接近.随机平均法只适用于弱阻尼和弱激励的情形.

而加权本质无振荡WENO方法,是近年来广泛流行的一种高分辨率数值方法,用于解决以对流为主的对流扩散方程,特别是双曲守恒律方程.WENO方法是在ENO方法的基础上采用加权思想构造的,用于求解包含激波、稀疏博以及接触间断等复杂结构的流体问题.WENO方法性能更稳定,对定常问题收敛性更好,它能够保证在解的光滑区精度更高,在解的间断去保持陡峭的间断过度和本质无振荡性质.WENO格式最初是在1994年由Liu,Osher和Chan提出,不同于ENO格式单一的模板选取,使用所有候选模板的凸组合,构造了一个三阶有限体积WENO格式,系统地讨论了WENO方法的构造过程和理论分析.随后在1996年Jiang和Shu在多维空间上给出了一个可以构造任意精度的有限差分WENO[9]格式的框架,并在其中设计了一个五阶精度的WENO格式,提出了光滑因子和非线性权构造的基本框架.至今,五阶精度的WENO格式是使用最广泛的,用来求解双曲守恒律方程WENO重构过程的标准格式.

本文针对上述问题,以及结合三阶TVD Runge-Kutta方法,提出了FPK方程的一种新的TVD Runge-Kutta Weno型差分方法,可以较好地解决其他方法所具有的不足,得到比较准确的概率密度函数.

1 具有随机外激非线性动力系统地FPK方程

对于非线性随机动力系统,其对应的FPK方程一般具有如下的形式：

(1)

FPK方程(1)是一个抛物型变系数偏微分方程,其描述了扩散过程的转移概率密度p(x,t|x0,t0)的进化或流动,其中ai,bij为对应的漂移和扩散系数.

当ai,bij均不显含时间t时,则FPK方程(1)可转化为：

(2)

FPK方程(2)是一个椭圆型变系数偏微分方程,常称为简化或平稳FPK方程.其解将是平稳概率密度p(x).要唯一确定FPK方程(1)的解,还需要初始条件和边界条件.

在本文中,采用初始条件：

p(x,t|x0,t0)=δ(x-x0),t=t0

(3)

其表示在t=t0时刻,系统以概率1处于初始状态x0.

无穷边界条件：

(4)

在随机振动理论中,FPK方程(1)与(2)常用来预测非线性随机动力系统的响应.因而,FPK方程解的精确程度对于可靠性分析起着至关重要的作用.

2 FPK方程的有限差分法

2.1 TVD Runge-Kutta格式

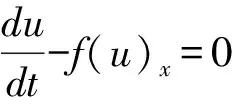
(5)

其中L(u)为f(u)x的逼近.对于半离散格式方程(5),标准Runge-Kutta时间离散是基于线性稳定性条件来实现格式的稳定性,此时CFL可以取较大的值.但是对于非线性方程,CFL必须很小才能保证格式的稳定性,由于高阶空间离散和低阶Runge-Kutta时间离散相互耦合,CFL必须大大低于线性稳定性要求,才会保证整个离散格式具有高阶精度和无振荡.本文中采用了具有TVD性质的三阶Runge-Kutta时间离散格式[7]：

u(1)=un+ΔtL(un)

其中un是第n时间层的守恒量,L(u) 是空间离散后的差分算子.

2.2 五阶WENO格式

设f(x)为一函数,则f′(xi)可以利用五阶WENO格式表示为：

(6)

其中:

IS0=13(a-b)2+3(a-3b)2,

IS1=13(b-c)2+3(b+c)2,

IS2=13(c-d)2+3(3c-d)2,

Δ+fk=fk+1-fk,Δ-fk=fk-fk-1

其中,ε为小量.

同样,

而对于f″(xi)利用四阶中心差分格式：

(7)

其中fi表示函数f(x)在点xi处的值,Δxi=xi+1-xi.

2.3 FPK方程的TVD Runge-Kutta WENO型差分格式

对于一维FPK方程(1),将微分的三阶TVD Runge-Kutta格式和微分方程的五阶WENO格式相结合,即可得到一维FPK方程的TVD Runge-Kutta WENO型差分格式.

一维问题的TVD Runge-Kutta WENO型差分格式：

(8)

其中：

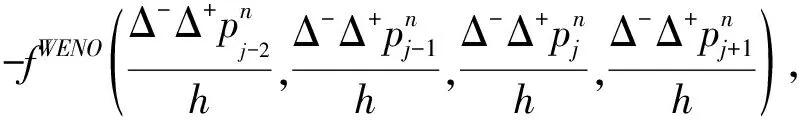
IS0=13(a-b)2+3(a-3b)2,

IS1=13(b-c)2+3(b+c)2,

IS2=13(c-d)2+3(3c-d)2,

其中,ε为小量.

3 数值算例

算例1考虑如下受随机外激的单自由度非线性系统：

(9)

其中ε=0.1 为常数,标识系统的非线性强度,W(t)是一零均值高斯白噪声,其相关系数为：E(W(t)W(t+τ))=2πS0δ(τ) ,S0为W(t)的谱密度,δ(τ)为Dirac函数.

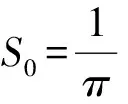
(10)

容易解得：

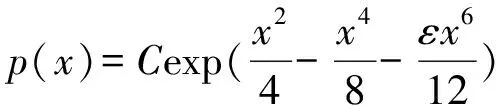
(11)

其中C为归一化常数.其精确解与本文方法的数值解对比如图1.

图1 精确解与本文数值解Fig.1 Exact solution and numerical solution in this paper

算例2考虑如下高斯白噪声参激和外激联合作用下的非线性振子：

X″+2αX′(1+γ1W1(t))+βX′(X2+X′2/ω2)+

ω2X(1+γ2W2(t))=γ3W3(t)

(12)

其中α,β为常数,ω为正常数,Wi(t)(i=1,2,3)为零均值的物理高斯白噪声,且相互独立满足E[Wi(t)Wi(t+τ)]=δi(τ)(i=1,2,3),δ为Dirac函数,γi(i=1,2,3) 表示各噪声强度.

图2 位移y1和速度y2 的边缘概率密度Fig.2 Marginal probability density of the displacement y1 and the velocity y2

4 结论

本文将三阶TVD Runge-Kutta方法和五阶WENO格式相结合,得到TVD Runge-Kutta WENO型差分格式,并将其成功地应用到随机外激作用下的非线性动力系统,获得了FPK方程的有限差分数值解,并与其解析解进行了比较.表明该方法的有效性以及可行性,并克服一般有限差分法的缺点,可以准确地获得更小的尾部概率密度,且无振荡,这对于可靠性分析至关重要.

1 Lin Y K, Cai G Q. Probabilistic structural dynamics: advanced theory and applications. New York: MeGraw-Hill, 1995

2 朱位秋. 非线性随机动力学与控制——Hamilton理论体系框架. 北京:科学出版社, 2003 (Zhu W Q. Nonlinear stochastic dynamics and controls——frame of Hamilton theory. Beijing: Science Press, 2003 (in Chinese))

3 赵超樱,潭维翰,郭志奇. 由菲简并光学参量放大系统获得压缩态光所满足的Fokker-Planck方程及其解. 物理学报, 2003,52:2694 (Zhao C Y, Tan W H, Guo Z Q. The solution of the Fokker-Planck equation of non-degenerate parametric amplification system for generation of squeezed light.ActaPhysicaSinica, 2003,52:2694 (in Chinese))

4 王平,杨新娥,宋小会. 具有含时平方反比项的谐振子的路径积分求解. 物理学报,2003,52:2957 (Wang P, Yang X E, Song X H. Exact solution for a harmonic oscillator with a time-dependent inverse square potential by path-integral.ActaPhysicaSinica, 2003,52:2957 (in Chinese))

5 徐伟,贺群,戎海武等. Duffing-Van der Pol振子随机分叉的全局分析. 物理学报,2003,52:1365 (Xu W, He Q, Rong H W,et al. Global analysis of stochastic bifurcation in a Duffing-van der Pol system.ActaPhysicaSinica, 2003,52:1365 (in Chinese))

6 孙中奎,徐伟,杨晓丽. 求解强非线性动力系统响应的一种新方法. 动力学与控制学报,2005(2):29～35 (Sun Z K, Xu W, Yang X L. A new analytic approximate technique for strongly nonlinear dynamic systems.JournalofDynamicsandControl, 2005,2(3):29～35 (in Chinese))

7 Wojtkiewicz S F, Bergman L A, Asce M. Numerical solution of high dimensional Fokker-Planck equations. 8th ASCE Specialty Conference on Probabilistic Mechanics and Structural Reliability, 2000

8 Sun Y, Kumar M. Numerical solution of high dimensional stationary Fokker-Planck equations via tensor decomposition and Chebyshev spectral differentiation.Computers&MathematicswithApplications, 2014,67(10):1960～1977

9 刘儒勋,舒其望. 计算流体力学的若干新方法. 北京:科学出版社,2003:42～106 (Liu R X,Shu Q W. Some new methods for computational fluid dynamics. Beijing:Science Press, 2003:42～106 ( in Chinese))

10 May 2016,revised 19 August 2017.