一类Lorenz型超混沌系统的Zero-Zero-Hopf分岔及共存吸引子研究*

陈玉明 陈春涛

(1.广东技术师范学院数学与系统科学学院, 广州 510665)(2.广西大学数学与信息科学学院, 南宁 530004)

引言

在1963年,Lorenz提出了首个混沌数理模型, 即Lorenz系统[1],这个系统起源于大气模型之中. 自此以后, 来至不同领域的数学家, 物理学家及工程师们对混沌的产生,混沌系统的特征, 分岔及通向混沌的路径等方面进行了深入的研究[2-5].

超混沌, 作为另一种复杂动力学行为, 它比混沌行为具有更强的复杂性, 并且在非传统工业及技术领域具有更强的应用潜力. 由于在自治常微分方程系统中要产生超混沌行为, 必须要求系统维数至少为四维, 因此, 对四维超混沌系统的研究, 尤其是对四维Lorenz型超混沌系统的研究[6,7],将显得尤为重要.

在三维混沌系统的研究中, 有很多研究者研究了系统平衡点的Zero-Hopf分岔现象,例如Guckenheimer[8], Han[9], Kuznetsov[10]及Llibre[11]等等. 从这些文献的研究可以看出,在一定的条件下, 从局部的Zero-Hopf平衡点处可以分岔出一些复杂的不变集, 也就是说, 在某些情况下, Zero-Hopf平衡点的出现便意味着“混沌”的产生. 在四维超混沌系统的研究中, 最近Cid-Montiel及Llibre等研究了一类超混沌Lorenz系统的Zero-Hopf分岔行为[12], 这是在中心流形维数大于等于4的系统中关于Zero-Hopf平衡点及分岔的首个工作. 即便到现在, 这类研究工作在四维及四维以上的系统中依然属于非常罕见.

混沌及超混沌系统的复杂性主要来源于混沌及超混沌吸引子的存在. 一般情形下, 相空间中只存在一个稳定的吸引子, 除了其它吸引子(都为不稳定)本身外, 从相空间中其它点出发的轨线都将趋向于那唯一的一个稳定的吸引子. 然而一些研究者最近发现了很多特殊的系统[14,15], 在这些系统中存在着各种不同稳定吸引子的共存现象, 这使得系统的相空间变得异常复杂, 尤其是这些不同稳定吸引子的吸引盆的边界.

通过对经典的Lorenz系统添加反馈控制, 本文得到如下的四维Lorenz型系统:

(1)

其中参数满足a>0,b>0,cder≠0. 当系统参数选取a=27.7,b=3.8,c=29.2,d=-1.5,e=-1.6及r=1.4时, 系统(1)具有超混沌吸引子, 该吸引子所对应的Lyapunov指数为:

λLE1=0.4157,λLE2=0.2479,λLE3=-0.0002,

λLE4=-32.2601.

该超混沌吸引子在x-y-z空间的投影相图如图1所示.

图1 系统(1)的超混沌吸引子在x-y-z空间的投影相图a=27.7,b=3.8,c=29.2,d=-1.5,e=-1.6及r=1.4Fig.1 Phase portrait of system (1) in the projection space of x-y-z,where a=27.7,b=3.8,c=29.2,d=-1.5,e=-1.6 and r=1.4

当系统参数满足br(c+d)(e+r)≤0时,系统(1)只具有唯一平衡点E0(0,0,0,0). 而当br(c+d)(e+r)>0时,系统(1)除了具有原点平衡点E0之外, 还将具有另外两个关于z轴对称的非原点平衡点.

针对四维Lorenz型超混沌系统(1),本文将研究该系统原点平衡点E0处发生的Zero-Zero-Hopf分岔行为(所谓Zero-Zer-Hopf平衡点, 是指具有两个零特征值以及一对纯虚特征值的孤立平衡点), 以及在某些特定参数下, 研究系统不同吸引子之间的共存现象.

1 Zero-Zero-Hopf分岔分析

考虑如下形式的微分方程系统:

(2)

其中ε∈(-ε0,ε0),ε0是充分小的正数, 函数F0,F1:R×Ω→Rn以及F2:R×Ω×(-ε0,ε0)→Rn都是C2类函数, 并且关于它们的第一个变量t都是周期T函数, 其中Ω是Rn中的一个子集. 在平均化理论的帮助下, 我们研究系统(1)中周期解的分岔问题, 其中主要的假设是未扰动系统:

(3)

具有一个周期解流形.

假设X(t,X0)是系统(3)满足条件X(0,X0)=X0=X(T,X0)的周期解, 于是系统(3)沿着周期解X(t,X0)的线性化系统可以写成:

(4)

并且记MX0(t)为线性微分方程(4)的基解矩阵.

假设存在开集V满足Cl(V)⊂Ω, 使得对于任意X0∈Cl(V),都有X(t,X0)为系统(3)中的一个周期为T的周期解. 其中集合Cl(V)被称为系统(3)的同步集, 这个集合完全是由周期解所构成. 包含在同步集Cl(V)中的周期解的分岔问题, 将由如下定理给出.

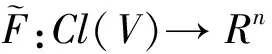
于是有如下结论成立:

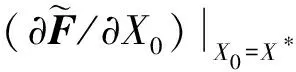
定理2:当满足条件d=a,b=0,r=0及a2+ac<0时, 四维Lorenz型超混沌系统(1)的原点平衡点E0为Zero-Zero-Hopf平衡点.

证明:容易计算得平衡点E0处的特征方程为:

P(λ)=(λ+b)(λ-r)(λ2+aλ-dλ-ac-ad)

(5)

定理3:令D=c(a-d)2e2-2(a+c)(a-d)e(a+e)r-(a+c)(a(a+c)-e2)r2≠0, 则四维Lorenz型超混沌系统(1)在原点平衡点E0处存在Zero-Zero-Hopf分岔. 在条件D1>0,D2>0,D3>0及D4>0下, 当原点经历Zero-Zero-Hopf分岔时, 在原点附近将会分岔出两条稳定的周期轨, 其中D1,D2,D3及D4如公式(10)所示.

证明:令ε为充分小的正参数,b1,d1及r1为非零实数. 在变换(b,d,r)→(εb1,a+εd1,εr1)的作用下,四维Lorenz型超混沌系统(1)将变形为:

(6)

进一步对变量进行重新标度, 令(x,y,z,w)T=(εu,εv,εp,εq)T, 并且将向量(u,v,p,q)T重新记为向量X=(x,y,z,w)T, 于是系统(6)可变为:

(7)

在定理1所描述的平均化理论的帮助下, 系统(7)的相关动力学行为将可以被研究. 考虑如下未扰动系统的初值问题:

(8)

未扰动系统(8)的解为X(t,X0)=(x(t),y(t),z(t),w(t)), 其中:

以及它的逆矩阵为:

基于上述矩阵, 计算定理1中的积分, 可得:

其中:

a(a+c)(x0-y0))z0+(a+c)·

(w0+cx0+ay0)d1-2(a+c)w0r1],

cey0+a(w0-ey0+c(x0+y0)))z0+

(a+c)(2w0+2ay0+c(x0+y0))d1-

2(a+c)w0r1],

2(a+c)2z0b1],

S0=(0,0,0,0),

其中解S0对应于原点平衡点E0. 针对另外两个解S±, 有如下关系式成立:

因此, 根据定理1, 存在系统(7)的两个周期为2π/m的周期解X+(t,ε)及X-(t,ε), 使得当ε→0时有X+(0,ε)→S+及X-(0,ε)→S-成立. 考虑到系统(6)与系统(7)的关系, 系统(7)的周期解X±(t,ε)分别对应着系统(6)的周期解εX±(t,ε).

P(S±)=λ4+c1λ3+c2λ2+c3λ+c4

(9)

其中:

2(a+c)e(a2-(2b+d)e+a(e-d))r-

(a+c)(a(a+c)-e2)r2],

令:

D4=c4D3

(10)

根据Routh-Hurwitz准则, 在条件D1>0,D2>0,D3>0及D4>0下, 特征多项式(9)的所有根都具有负实部, 也就是说, 在原点E0处由Zero-Zero-Hopf分岔所产生的两个周期解X+(0,ε)→S+及X-(0,ε)→S-都是稳定周期解.

2 共存吸引子研究

选取恰当的系统参数, 通过详细的数值分析, 可发现系统(1)存在多种吸引子共存的现象, 即同组参数条件下, 系统(1)满足不同初始条件的解有可能呈现出完全不同的动力学行为. 具体可包括超混沌吸引子与周期吸引子的共存, 不同周期吸引子之间的共存等.

固定参数a=23.96,b=4.39,c=26.82,d=-1.38,e=-0.99及r=1.43, 对初始条件(61,68,58,-40), 系统(1)的解将会收敛于一个周期解, 其在y-z-w空间的投影如图2(a)所示, 该周期吸引子所对应的Lyapunov指数为:λLE1=0.0000,λLE2=-0.0015,λLE3=-0.0015,λLE4=-28.2961.

在同一组参数下, 对于初始条件(58,55,33,-52), 系统(1)的解则收敛于一个超混沌吸引子, 在y-z-w空间的投影相图如图2(b)所示, 该超混沌吸引子所对应的Lyapunov指数为:λLE1=0.2521,λLE2=0.0708,λLE3=0.0000,λLE4=-28.6218.

因此, 当参数满足a=23.96,b=4.39,c=26.82,d=-1.38,e=-0.99及r=1.43时, 系统(1)的相空间中存在着超混沌吸引子与周期吸引子的共存, 其在y-z-w空间的投影如图2(c)所示.

类似的, 当固定参数a=28.67,b=3.52,c=25.16,d=-1.86,e=-1.15及r=1.15时, 也存在吸引子的共存现象. 对初始条件(73,-97,3,-73), 系统(1)的解将会收敛于一个周期解, 其在y-z-w空间的投影如图3(a)所示, 该周期吸引子所对应的Lyapunov指数为:λLE1=0.0000,λLE2=-0.0817,λLE3=-0.4814,λLE4=-32.3287.

在同一组参数下, 对于初始条件(-57,-82,8,80), 系统(1)的解则收敛于另一个周期吸引子, 在y-z-w空间的投影相图如图3(b)所示, 该周期吸引子所对应的Lyapunov指数为:λLE1=-0.0003,λLE2=-0.0535,λLE3=-0.0535,λLE4=-32.7843.

图2 系统(1)共存吸引子的y-z-w空间投影, a=23.96,b=4.39,c=26.82,d=-1.38,e=-0.99,r=1.43Fig.2 Projections of coexisting attractors in y-z-w space for system(1),wherea=23.96,b=4.39,c=26.82,d=-1.38,e=-0.99,r=1.43

图3 系统(1)共存吸引子的y-z-w空间投影, a=28.67,b=3.52,c=25.16,d=-1.86,e=-1.15,r=1.15Fig.3 Projections of coexisting attractors in y-z-w space for system(1), wherea=28.67,b=3.52,c=25.16,d=-1.86,e=-1.15,r=1.15

因此, 当参数满足a=28.67,b=3.52,c=25.16,d=-1.86,e=-1.15及r=1.15时, 系统(1)的相空间中则存在着两个不同的周期吸引子的共存, 其在y-z-w空间的投影如图3(c)所示.

3 结论

通过对经典的Lorenz混沌系统施加反馈控制方法, 本文得到了一类四维Lorenz型超混沌系统,并从局部和全局两个方面对该新超混沌系统的动力学行为进行了研究. 首先, 在局部动力学方面, 基于平均化理论方法, 研究了该系统在原点平衡点处发生的Zero-Zero-Hopf分岔行为, 得到了系统在原点发生Zero-Zero-Hopf分岔的参数条件, 证明了两条周期轨的存在性, 并且给出了它们的稳定性条件. 其次, 在全局动力学方面, 借助数值模拟方法, 发现该系统在某些特定参数条件下存在着除了平衡点以外的不同吸引子之间的共存现象, 比如超混沌吸引子与周期吸引子共存, 不同周期吸引子之间的共存, 等等.

1Lorenz E N. Deterministic non-periodic flow.JournaloftheAtmosphericSciences, 1963,20:130～141

2Hirsh M W, Smale S, Devaney R L. Differential equations,dynamical systems, and an introduction to chaos. New York:Elsevier Academic Press, 2007

3Shilnikov L P, Shilnikov A L, Turaev D V, et al. Methods of qualitative theory in nonlinear dynamics. Singapore:World Scientific, 2001

4Wiggins S. Introduction to applied nonlinear dynamical systems and chaos(2nd edition). New York:Springer-Verlag, 1990

5Hastings S, Troy W. A shooting approch to chaos in the Lorenz equations.JournalofdifferentialEquations, 1996,127:41～53

6Stenflo L. Generalized Lorenz equations for acoustic-gravity waves in the atmosphere.PhysicaScripata, 1996,53:83～84

7Chen Y, Yang Q. Dynamics of a hyperchaotic Lorenz-type system.NonlinearDynamics, 2014,77:569～581

8Guckenheimer J. On a codimension two bifurcation. In: Lecture Notes in Math, 1980,898:99～142

9Han M. Existence of periodic orbits and invariant tori in codimension two bifurcations of three dimensional systems.JournalofSystemsScienceandMathematicalSciences, 1998,18:403～409

10 Kuznetsov Y A. Elements of applied bifurcation theory(3rd edition). Berlin:Spring, 2004

11 Llibre J, Chavela E P. Zero-Hopf bifurcation for a class of Lorenz-type systems.Discrete&ContinuousDynamicalSystems-SeriesB, 2014,19:1731～1736

12 Montiel L C, Llibre J, Stoica C. Zero-Hopf bifurcation in a hyperchaotic Lorenz system.NonlinearDynamics, 2014,75:561～566

13 周艳,张伟. 复合材料层合板的双Hopf分叉分析. 动力学与控制学报, 2015,13(3):161～164 (Zhou Y, Zhang W. Double Hopf bifurcation of composite laminated thin plate.JournalofDynamicsandControl, 2015,13(3):161～164(In Chinese))

14 Chen Y, Yang Q. A new Lorenz-type hyperchaotic system with a curve of equilibria.MathematicsandComputersinSimulation, 2015,112:40～55

15 Wei Z. Dynamical behaviors of a chaotic system with no equilibria.PhysicsLettersA, 2011,376:102～108