基于Melnikov方法的单自由度干摩擦振子的混沌分析*

秦琅 谢建华

(西南交通大学力学与工程学院, 成都 610031)

引言

工程与实际生产问题中干摩擦因素是广泛存在的,如制动系统和机床切削系统的干摩擦.干摩擦具有非线性效应,使得系统可能产生复杂的动力学行为,可能产生自激振动,多周期现象,甚至会出现混沌现象.Hetzler等[1]基于Stribeck干摩擦模型研究了单自由度与两自由度干摩擦系统的稳定性与Hopf分岔.Guo和Xie[2]研究了单自由度干摩擦受迫系统共振时的NS分岔.Van de Vrande和De Kraker[3]研究了干摩擦引起的粘滑振动现象.Melnikov方法是研究在弱周期力激励下近Hamilton系统中的混沌运动的较为有效的解析方法[4,5].一些工程实际问题,可以将其简化为带有弱周期扰动项的具有同宿轨道或者异宿轨道的二阶常微分方程.通过建立Poincaré映射,就可以采用Melnikov方法进行解析计算.许多学者采用Melnikov方法解决一些具有实际工程背景问题,取得了很好的结果.Wu和Mccue[6]利用扩展的Melnikov方法分析单自由度船舶模型的摇摆运动,研究了不同波浪模型对船舶摇摆运动的影响.韩宁,曹庆杰[7]基于Melnikov函数研究了柱面系统的混沌动力学行为.贺尚宏[8]将Melnikov方法应用于确定多参数机械系统的混沌边缘中.文献[9,10]以两边受约束倒置的单摆为模型,应用扩展的Melnikov方法研究了其动力学行为.文献[11,12]研究了单自由非线性的传送带系统,即系统的弹簧为非线性的.分析了传送带速度与摩擦力振幅改变对于系统的动力学行为的影响.本文的研究模型与其相似,但是采用线性弹簧,构造出几何非线性系统,籍此分析系统相应的动力学行为,并应用Melnikov方法给出了系统的混沌解析预测得到出现马蹄型混沌运动的条件,并将Melnikov解析结果同数值结果进行比对,相互印证,说明了Melnikov解析结果的有效性.

1 力学模型与运动方程

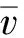
FT=-2Tsinθ

=(-2T0/l)x+(T0-kl)x3/l3+o(x3)

(1)

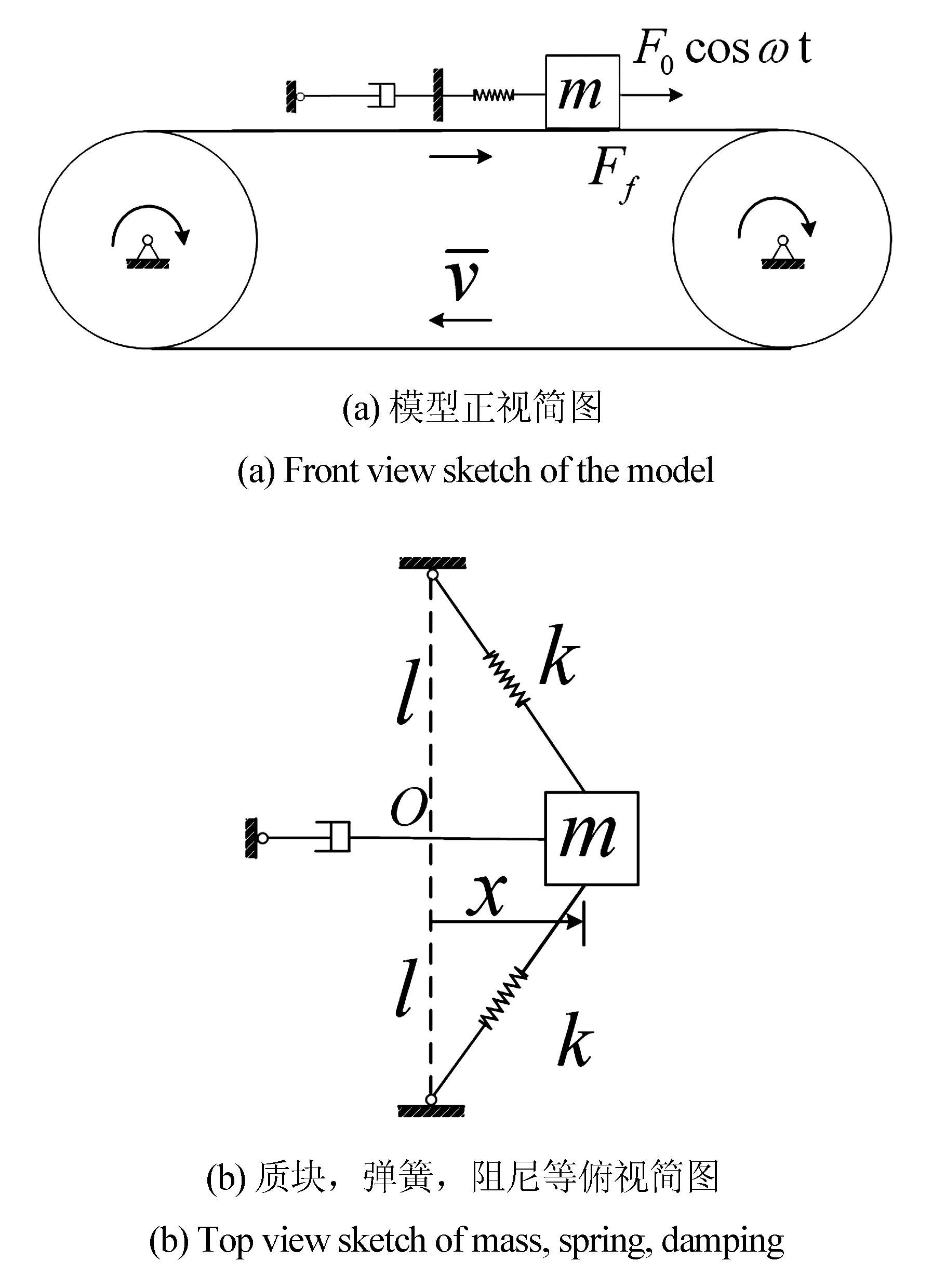
图1 力学模型图Fig.1 Mechanical model

质块的运动微分方程为：

(2)

其中a=-2T0/ml,b=(kl-T0)/ml3,F0=εmγ,c=εmα,f0=εmβ,ε为小参数,假定系统参数a,b,α,β,γ,ω均为正值,略去o(x3)项,进一步将系统(2)化为微分方程组的形式：

(3)

当ε=0时,未扰系统:

(4)

为Hamilton系统.未扰系统(4)Hamilton量为:

(5)

q0(t) =(x0(t),v0(t))

(6)

2 Melnikov方法分析

系统(3)的Melnikov积分为:

(7)

v0(t-t0)(α·v0(t-t0)+

(8)

令τ=t-t0,则有:

(9)

(10)

(11)

对于积分I2可以首先得出:

(12)

sech2x+tanh2x=1

可得:

(13)

最后得出:

(14)

由此可得,Melnikov积分:

(15)

将式(15)中的α,β,γ分别用εα,εβ,εγ替换,得到M(t0)具有简单零点的条件:

(16)

3 数值模拟

由分岔图,相图可以看出,随着外激励εγ的变化,系统表现出复杂的动力学行为.当εγ=0.53时,位于Melnikov函数阈值曲线下侧,系统处于周期一运动.随着εγ的不断增加,系统进入了周期倍化阶段.当εγ=0.61,εγ=0.625,εγ=0.64时,均位于Melnikov函数阈值曲线上侧.当εγ=0.61时,系统处于周期二运动,见图4(b) .当εγ=0.625时,系统做周期四运动,见图4(c).随着εγ进一步增大系统最终步入混沌运动状态,当εγ=0.64时,系统处于混沌运动状态,见图4(d).图5(b)表明εγ=0.64时,系统的最大Lyapunov指数大于零,证实了系统处于混沌状态,这符合Melnikov函数阈值曲线结果.数值结果与解析结果相符.

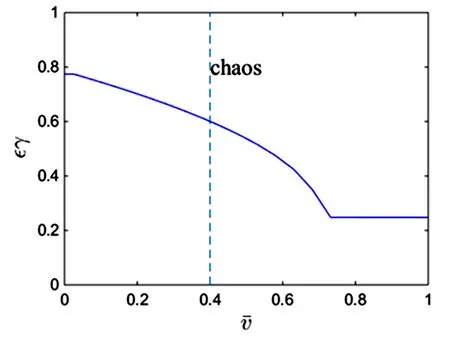
图2 Melnikov函数阈值曲线Fig.2 Criteria curve of Melnikov function

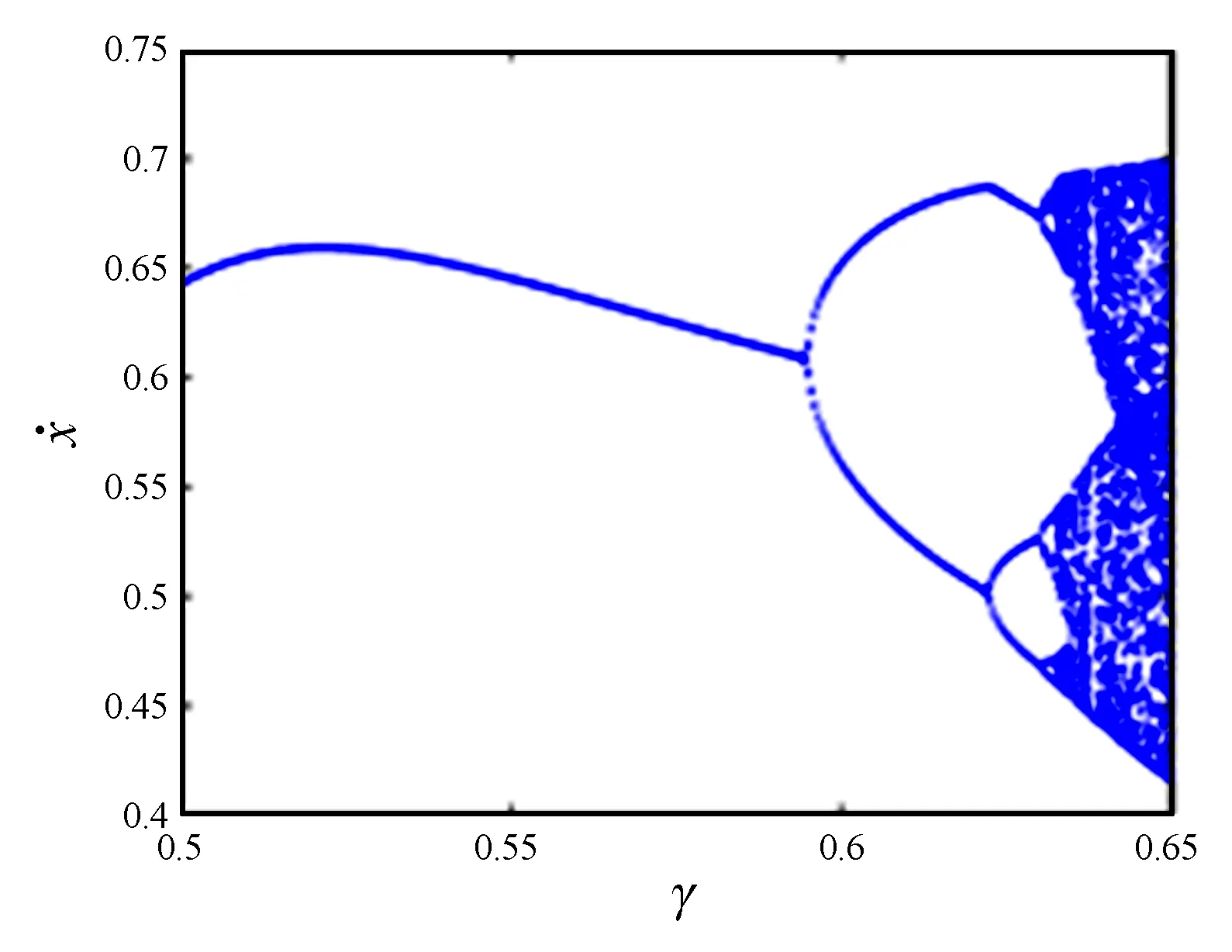
图3 分岔图Fig.3 Bifurcation diagram

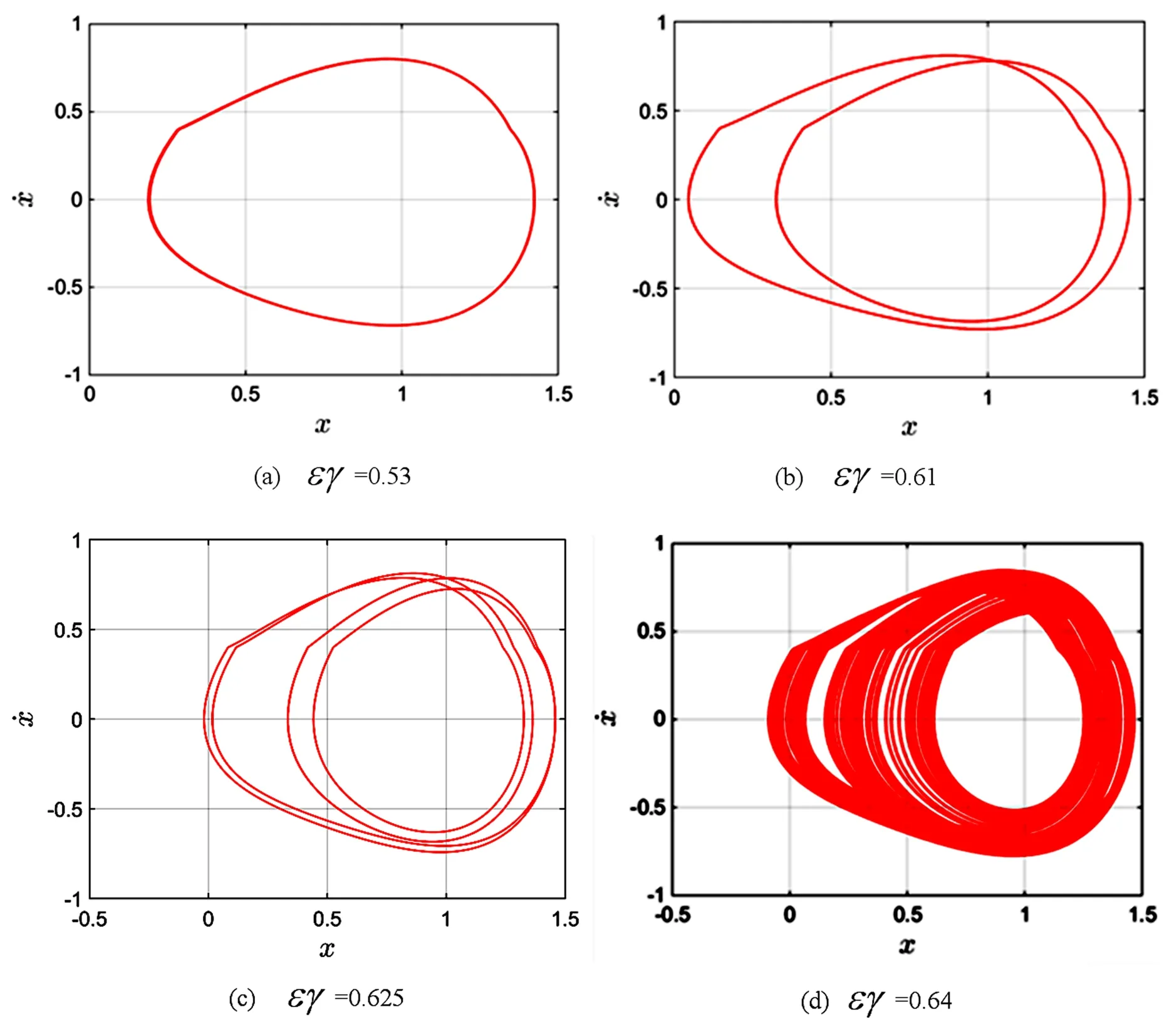
图4 εγ变化时系统相图Fig.4 System phase diagrams when εγ changes

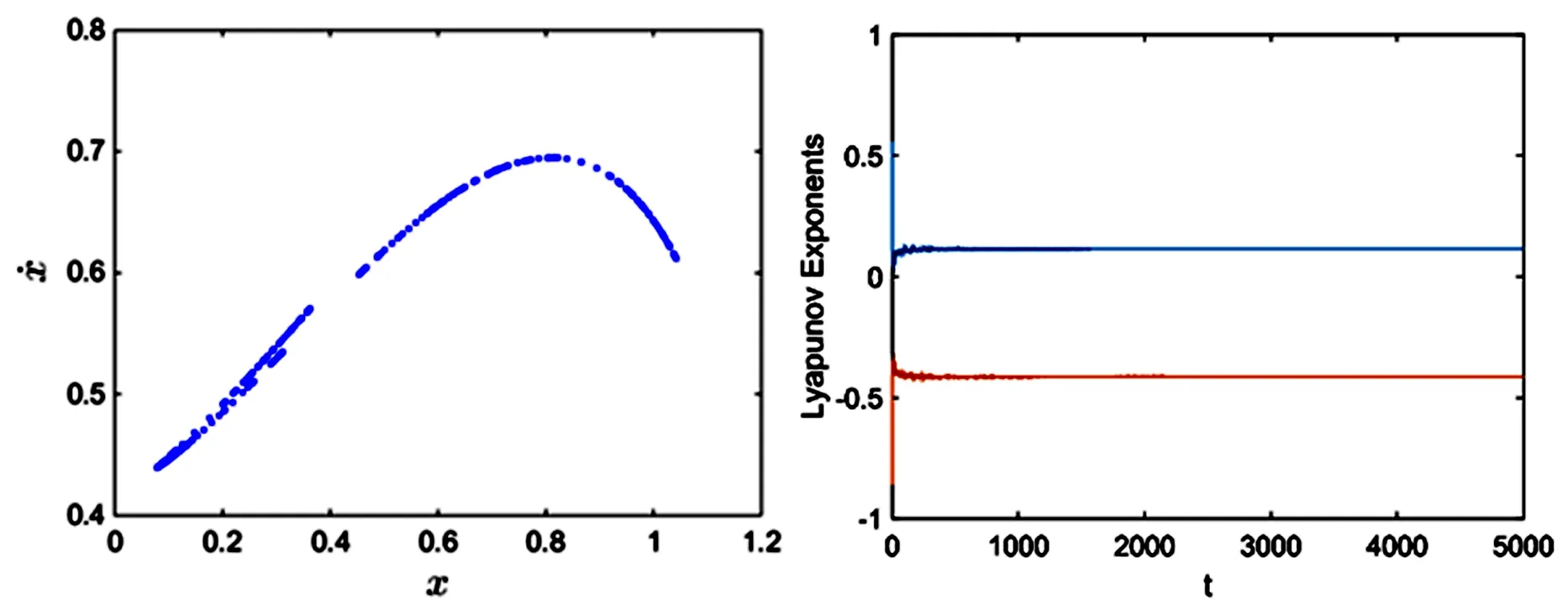
图5 εγ=0.64系统Poincaré截面图(a), Lyapunov指数(b)Fig.5 (a) Poincare cross section, and (b) Lyapunov exponent, when εγ=0.64

4 结语

Melnikov方法是判断系统是否具有马蹄型混沌的有效的解析方法,本文运用Melnikov方法对一个单自由度干摩擦振子进行分析,得出了系统产生马蹄型混沌的条件.通过相图,Poincaré截面图和分岔图等手段,证明了数值结果与通过Melnikov方法得到的解析结果相符.研究表明在一定参数条件下随着外激励的幅值逐渐增加,系统由周期运动经历周期倍化过程逐渐步入混沌运动.

1Hetzler H, Schwarzer D, Seemann W. Analytical investigation of steady-state stability and Hopf-bifurcations occurring in sliding friction oscillators with application to low-frequency disc brake noise.CommunicationsinNonlinearScience&NumericalSimulation, 2007,12(1):83～99

2Guo Y, Xie J H. Neimark-Sacker (N-S) bifurcation of oscillator with dry friction in 1∶4 strong resonance.AppliedMathematicsandMechanics, 2013,34(1):27～36

3Vrande B L V D, Campen D H V, Kraker A Dl. An approximate analysis of dry-friction-induced stick-slip vibrations by a smoothing procedure.NonlinearDynamics, 1999,19(2):159～171

4刘曾荣. 混沌的微扰判据. 上海:上海科技教育出版社, 1994 (Liu Z R. Perturbation criterion of chaos. Shanghai:Shanghai Scientific and Technological Education Publishing House, 1994 (in Chinese))

5李继斌,陈凤娟. 混沌,Melnikov方法及新发展. 北京:科学出版社, 2012:125～131 (Li J B, Chen F J. Chaos, Melnikov method and new development. Beijing:Science Press, 2012:125～131 (in Chinese))

6Wu W, Mccue L. Application of the extended Melnikov′s method for single-degree-of-freedom vessel roll motion.OceanEngineering, 2008,35(17):1739～1746

7韩宁,曹庆杰. 一类典型柱面系统的非线性动力学分析. 全国非线性动力学和运动稳定性学术会议. 2013 (Han N, Cao Q J. Nonlinear dynamic analysis of a typical cylindrical system. In:National Conference on nonlinear dynamics and stability of motion. 2013 (in Chinese))

8贺尚宏. Melnikov方法在确定多参数机械动力系统混沌边缘中的应用[硕士学位论文]. 成都:西南交通大学, 2015 (He S H.On the application of Menikov Method to determinting edge of chaos of mechanical dynamic system with muti-parametersr[Master Thesis]. Chengdu:Southwest Jiaotong University, 2015 (in Chinese))

9Du Z, Zhang W. Melnikov method for homoclinic bifurcation in nonlinear impact oscillators.Computers&MathematicswithApplications, 2005,50(3):445～458

10 Du Z, Li Y, Shen J, et al. Impact oscillators with homoclinic orbit tangent to the wall.PhysicaDNonlinearPhenomena, 2013,245(1):19～33

11 Luo A C J, Huang J. Discontinuous dynamics of a non-linear, self-excited, friction-induced, periodically forced oscillator.NonlinearAnalysisRealWorldApplications, 2012,13(1):241～257

12 李群宏,闫玉龙,韦丽梅等. 非线性传送带系统的复杂分岔. 物理学报, 2013,62(12):120505～10 (Li Q H, Yan Y L, Wei L M, et al. Complex bifurcations in a nonlinear system of moving belt.ActaPhysicaSinica, 2013,62(12):120505～10 (in Chinese))

13 Olsson H, Åström K J, Wit C C D, et al. Friction models and friction compensation.EuropeanJournalofControl, 1998,4(3):5517～5522