含间隙限位约束梁结构频响特征的实验研究

万雨婷 孙樱

(复旦大学航空航天系, 上海 200433)

引言

现代制造业的发展对机构提出了越来越高的性能要求,工程中存在大量复杂的振动问题需要解决,这要求对机构的动力学特性有全面的了解和掌握.尽管线性振动理论发展已经完善,但其只适用于小变形情形,超过此范围,则必须考虑非线性因素.非线性的出现使得机构的运动超出线性控制规律的预测,可能导致机构在运动中出现失效.例如美国的Hubble太空望远镜于1990年入轨后,热循环引起的太阳能帆板的“卡死一滑动”周期性运动,导致了对定点的扰动[1]；我国发射的东三卫星由于铰关节间隙非线性的存在,出现了颤振[2].随着科学技术的发展,研究人员已开始深入分析非线性动力学的多种现象规律及非线性因素引起的振动对系统产生的动力学影响,使系统动态设计与运行可以满足日益提高的精度需求.

国内外学者对非线性系统动力学特性研究做了一系列的工作,取得一定研究成果.常见的非线性模型分为光滑非线性和非光滑非线性.在光滑非线性系统研究中国内外学者已有成熟的工作.王珺等[3]通过仿真计算研究了预变形对非线性结构响应特征的影响,数值计算结果显示出随着预变形的逐渐增大,非线性结构频响特征呈现从硬特性向软特性的转变,并求出了转变过程的临界变形；赵环迪等[4]通过实验方法研究了预变形对梁结构的振动响应的影响,结果表明随着预变形单一方向上的增加,主梁结构呈现先硬后软的刚度特性；Ozge Arslan等[5,6]通过实验定位、辨识振动系统非线性参数的方法,把实验辨识的参数用于仿真建立数学模型,将仿真与实验所得结果进行对比,验证了仿真建模的准确性；颜科鹏等[7]通过实验研究了梁的预变形和激励力的幅值对结构多稳态响应特征的影响规律,同时还考虑了螺母扭矩、边界条件及实验过程中扫频速度等因素对梁的结构振动的影响,揭示了含非线性柔性约束梁的多稳态振动特性随预变形和外界激励的变化.

在非线性系统研究中人们讨论最多的是非线性与非光滑因素同时存在的情形,非光滑动力学系统比光滑动力学系统具有更多样更复杂的动力学行为,非光滑非线性动力系统大体可分为三类：由干摩擦引起的动力学系统、分段光滑系统、由碰撞引起的非光滑系统[8].在上世纪六七十年代开始,研究者们利用一种新的方法对非线性非光滑系统动力学响应进行深入分析,这种方法即Poincare的映射方法[9]；Han和Luo等[10]采用数值仿真方法计算了含有冲击系统结构的动力学响应,最后给出了非线性结构的相曲线和Poincare图.研究人员发现其不但具有与光滑系统相似的动力学行为,还含有很多特有的复杂现象,比如许多边界碰撞分岔现象(如擦边、跳跃、角点、切换、粘滞等).Yoshitake等[11]对非光滑非线性系统的分岔特性进行了研究,得出了非光滑非线性结构运动产生分岔和混沌的条件；陈思雨等[12]初次研究了齿轮传动非线性动力学的周期解的形成过程及在非光滑非线性系统呈现的冲击分岔行为.间隙的存在是使系统产生非光滑非线性的主要原因,阎绍泽等[13]对一可展结构进行了实验研究,结果表明间隙和摩擦的存在导致了结构的非线性,且实验测得的结构固有频率较有限元模型要小；Kahraman 和Blankenship[14]通过实验观察到在一对齿轮啮合间隙的非线性模型中存在混沌现象.国内外基于不同的工程背景,对含间隙结构的动态特性,应用不同方法开展了一系列研究,研究的主要方向有齿轮间间隙非线性动力学、航天器中含间隙机构动力学以及其他关于含间隙结构非线性特性等一系列问题.曹妍妍等[15]以受间隙约束的悬臂梁结构为实验模型,研究该系统在简谐激励下接触刚度与外激励影响的非线性动态响应；I.R. Praveen Krishna C. Padmanabhan[16]通过实验与仿真计算研究了含双面间隙结构中的连接刚度,连接材料及间隙距离对非线性动力学行为的影响；孙东阳等[17]利用非线性弹簧阻尼模型建立了谐波齿轮传动的含间隙机构的接触碰撞动力学模型,结果表明谐波齿轮传动和机械部件柔性对间隙碰撞都有缓冲效果；谷勇霞等[18]对含多间隙帆板展开过程进行了研究,通过帆板展开过程中角速度的变化,分析了间隙碰撞对展开机构的稳定性的影响；胡世武等[19]通过实验与仿真讨论了间隙尺寸、激励频率和外激励力幅值对接触碰撞力的影响.

本文从实验角度深入研究了含间隙限位非线性梁结构的非线性动力学响应的变化,研究了含间隙非线性梁结构的动力学响应随外激励幅值大小以及间隙宽度大小变化的关系.通过实验研究得到了丰富的实验现象,为理论仿真计算提供了依据,促进了非线性理论的进一步发展.

1 实验方法及参数设计

1.1 实验设置

实验由实验平台、功率放大器、激振器、加速度传感器、力传感器、试件和数据控制采集系统组成.实验振动仪采用亿恒振动控制器VT-9008,振动台系统包括TIRA BAA120型号功率放大器和TIRA S-51110M型号激振器,激振器最大激振力为100N,振动最大频率为5000Hz,符合实验要求.

试件主梁铸钢件经过先铸造后调质处理,使其强度塑性和韧性得到加强,具有较好的综合机械性能,满足实验要求.试件片梁钢件采用线切割加工而成.试件主梁及片梁的几何参数见表1.

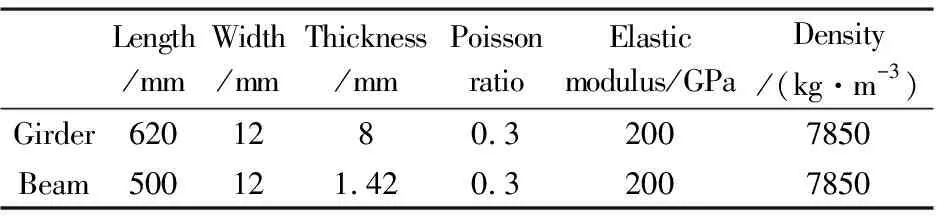
表1 试件结构参数Table 1 Structural parameters of the specimens

试件为一矩形截面主梁及一片薄片梁组成.主梁一端用压块固定,另一端自由,形成固支梁.在靠近主梁自由端30mm位置下方水平放置一薄片梁,两者形成间隙,组成含间隙限位的非线性结构.薄片梁两端用压块固定住,通过在薄片梁两端的下方垫放钢尺从而改变薄片梁竖直高度,进而改变薄片梁与主梁之间的间隙距离大小,垫放钢尺数量越多薄片梁距离主梁距离越近,间隙距离越小.实验结构如图1所示.

图1 实验系统图Fig.1 Experimental system diagram

实验过程采用的是恒力幅的正弦扫频激励实验,扫频方式为线性扫频,扫频速度为1Hz/min.在距离主梁自由端附近6mm位置连接一个加速度传感器,采集输出信号.在距离主梁自由端262mm位置连接激振器—力传感器,控制输出力的大小.正弦扫频实验采用振动控制采集仪,一通道连接力传感器,另一通道连接加速度传感器；定频测量时域信号同时采用振动控制仪与数据采集分析仪,力传感器连接振动控制仪,加速度传感器连接数据采集分析仪.实验结构示意图如图2所示.

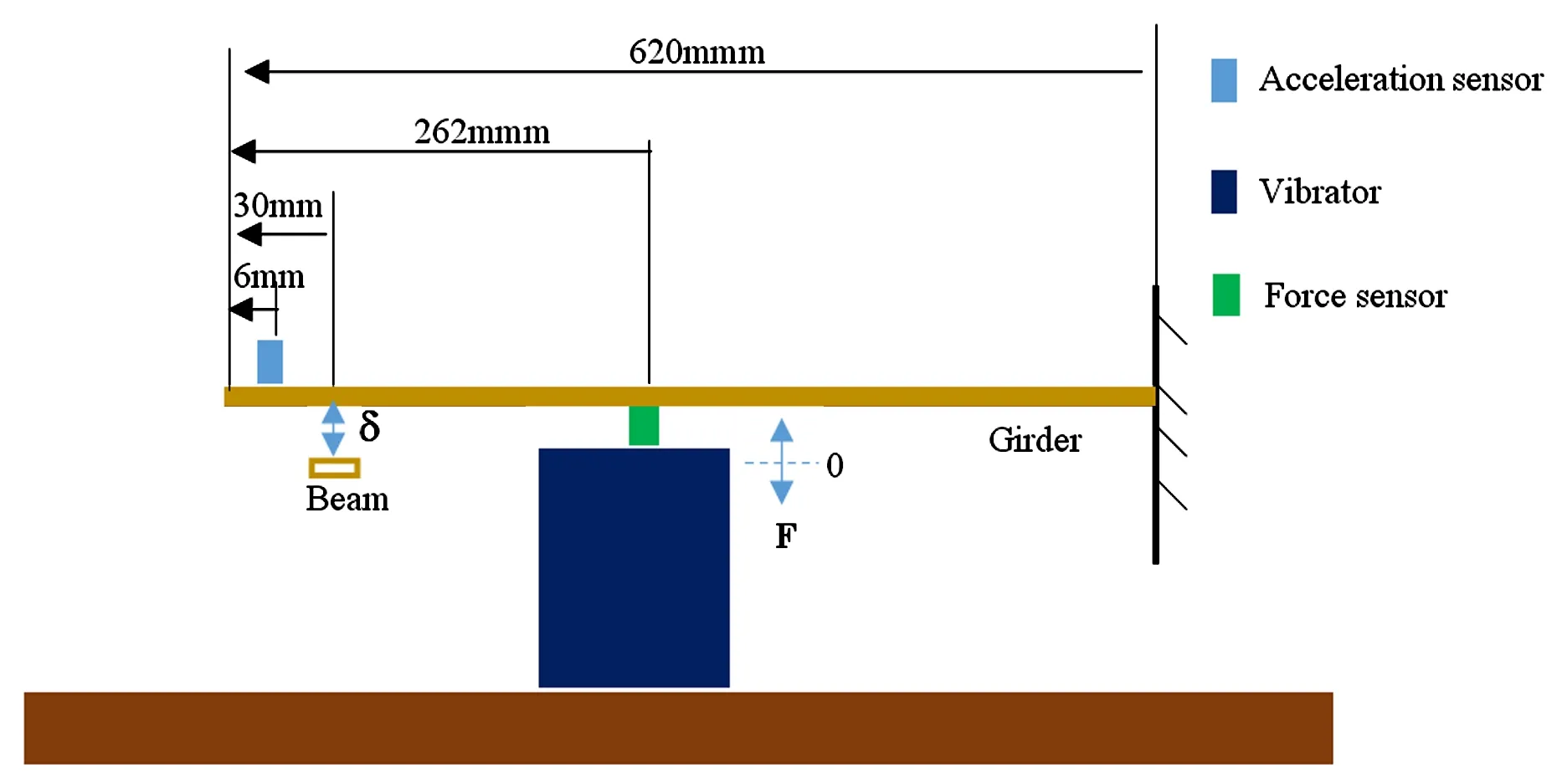
图2 实验结构示意图Fig.2 Experimental structure diagram

1.2 实验参数设计

本文主要研究了两个参数：外激励幅值大小与间隙距离大小的改变对含间隙限位非线性梁结构动力学特性的影响.其中,通过控制仪器改变外激励力幅值(F),外激励力的幅值变化取值0.2N-0.4N-0.6N-0.8N-1.0N-1.2N-1.4N-1.6N-1.8N-2.0N；通过垫放在薄片梁下面的钢尺片数(n)改变薄片梁竖直高度,垫1片钢尺时测得实际间隙距离为7.8mm,垫2片钢尺时测得间隙距离为7.1mm,垫3片钢尺时测得间隙距离为6.3mm,垫4片钢尺时测得间隙距离为4.7mm,通过钢尺数量改变薄片梁与主梁之间的间隙距离大小.

2参数改变对含间隙限位非线性梁振动特性的影响

2.1 改变力幅值大小的实验结果

1片钢尺(间隙距离7.8mm)——外激励幅值分别从0.2N-0.4N-0.6N-0.8N-1.0N-1.2N-1.4N-1.6N-1.8N-2.0N改变,频响曲线随外激励幅值改变如图3所示.

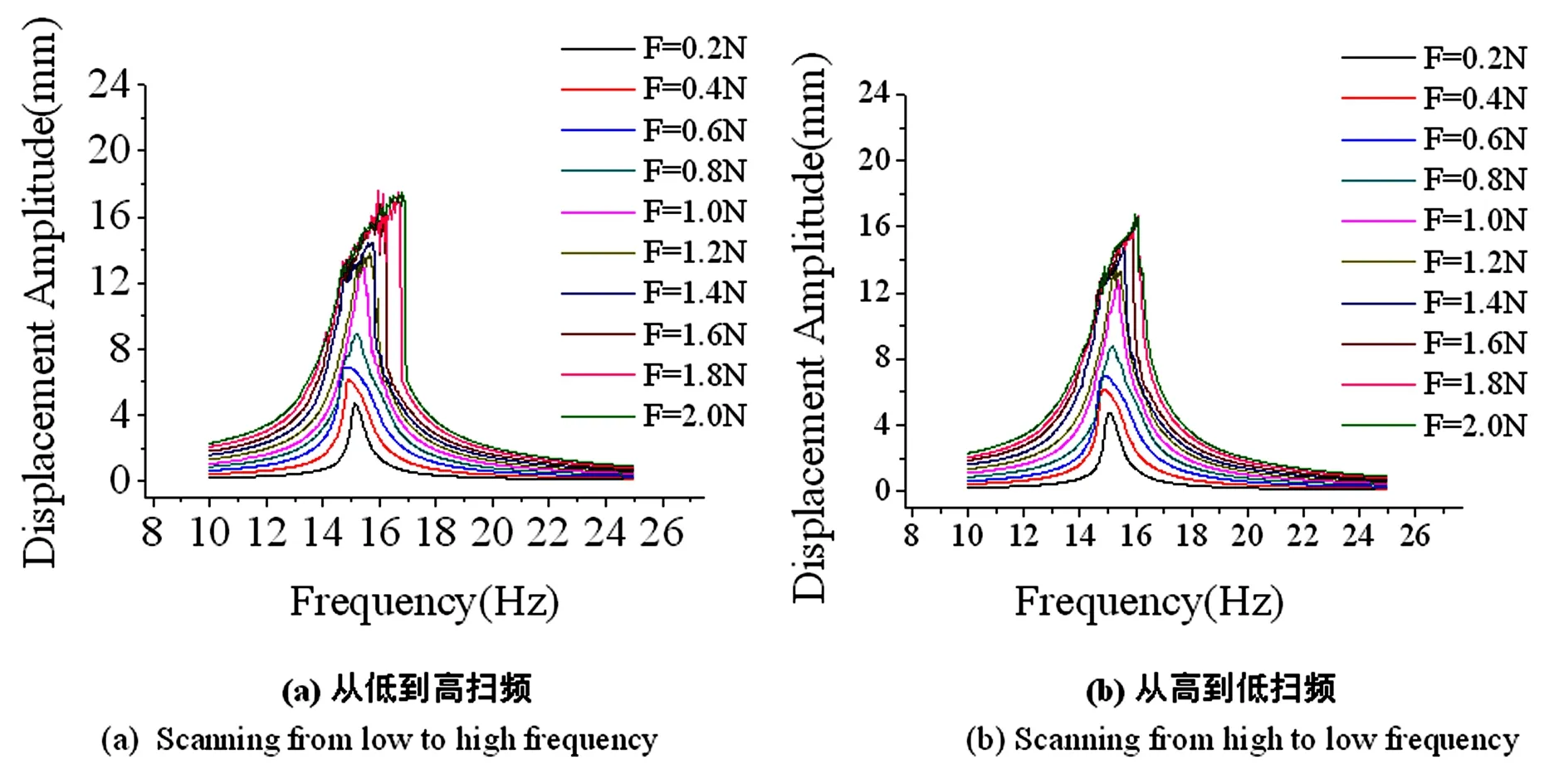
图3 从低到高-从高到低扫频位移频响曲线Fig.3 Frequency response curves when scanning from low to high and high to low frequency

由图3实验结果可得,位移响应曲线的跳跃频率出现先变低再变高,结构在低力幅值0.2N-0.4N-0.6N呈现先变软特性,分析由于在主梁未与薄片梁发生碰撞时结构呈线性状态,随着外激励力的增大,结构中出现立方钢度非线性因素使结构跳跃频率变小,且呈现变软特征,随着力幅值增大结构发生碰撞等效接触刚度变大,从而出现变硬的特性.

2片钢尺(间隙距离7.1mm)——外激励幅值分别从0.2N-0.4N-0.6N-0.8N-1.0N-1.2N-1.4N-1.6N-1.8N-2.0N改变,频响曲线随外激励幅值改变如图4所示.

图4 从低到高-从高到低扫频位移频响曲线Fig.4 Frequency response curves when scanning from low to high and high to low frequency

由图4可知,结构在外激励力幅值较小时0.2N-0.4N主梁与薄片梁未发生碰撞同样出现先变软的特征,随着力幅值增大主梁与薄片梁发生碰撞,接触刚度变大,结构出现变硬特征.

3片钢尺(间隙距离6.3mm)——外激励幅值分别从0.2N-0.4N-0.6N-0.8N-1.0N-1.2N-1.4N-1.6N-1.8N-2.0N改变,频响曲线随外激励幅值改变如图5所示.

图5 从低到高-从高到低扫频位移频响曲线Fig.5 Frequency response curves when scanning from low to high and high to low frequency

4片钢尺(间隙距离4.7mm)——外激励幅值分别从0.2N-0.4N-0.6N-0.8N-1.0N-1.2N-1.4N-1.6N-1.8N-2.0N改变,频响曲线随外激励幅值改变如图6所示.

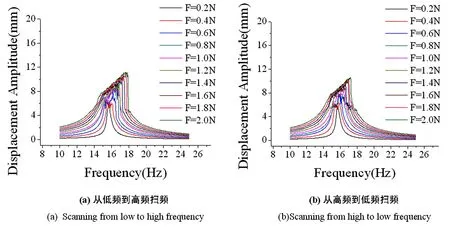
图6 从低到高-从高到低扫频位移频响曲线Fig.6 Frequency response curves when scanning from low to high and high to low frequency

由图5、图6实验结果可以看出,在间隙距离较小时,随着外激励幅值的不断增大,主梁与薄片梁碰撞发生接触,接触刚度变大,位移响应曲线出现跳跃频率变大,结构逐渐变硬的特征.

在不同间隙距离下改变外激励幅值的实验结果可以发现有着相似的规律.随着外激励幅值的不断增大,从低频到高频扫频和从高频到低频扫频时,位移频响曲线跳跃频率均出现变大的特性,实验中观察到由于在外激励幅值较小时,主梁与薄片梁未发生碰撞,结构为线性状态,在主梁与薄片梁发生碰撞后,结构等效接触刚度增大,出现频率漂移的特性.

2.2 改变间隙宽度大小的实验结果

F=0.2N——改变间隙宽度大小(间隙距离1片钢尺7.8mm—2片钢尺7.1mm—3片钢尺6.3mm—4片钢尺4.7mm),位移响应曲线如图7所示.

图7 改变间隙大小从低到高扫频位移频响曲线Fig.7 Frequency response curves when scanning from low to high frequency under different clearance distance

由图7实验曲线可以得知,在0.2N时,垫1-4片钢尺(间隙距离4.7mm—6.3mm—7.1mm—7.8mm),位移频响曲线没有出现跳跃现象,故在外激励幅值较小时,主梁与薄片梁未发生碰撞,系统动态特性仍为线性系统.

F=0.4N——改变间隙宽度大小(间隙距离1片钢尺7.8mm—2片钢尺7.1mm—3片钢尺6.3mm—4片钢尺4.7mm),位移响应曲线如图8所示.

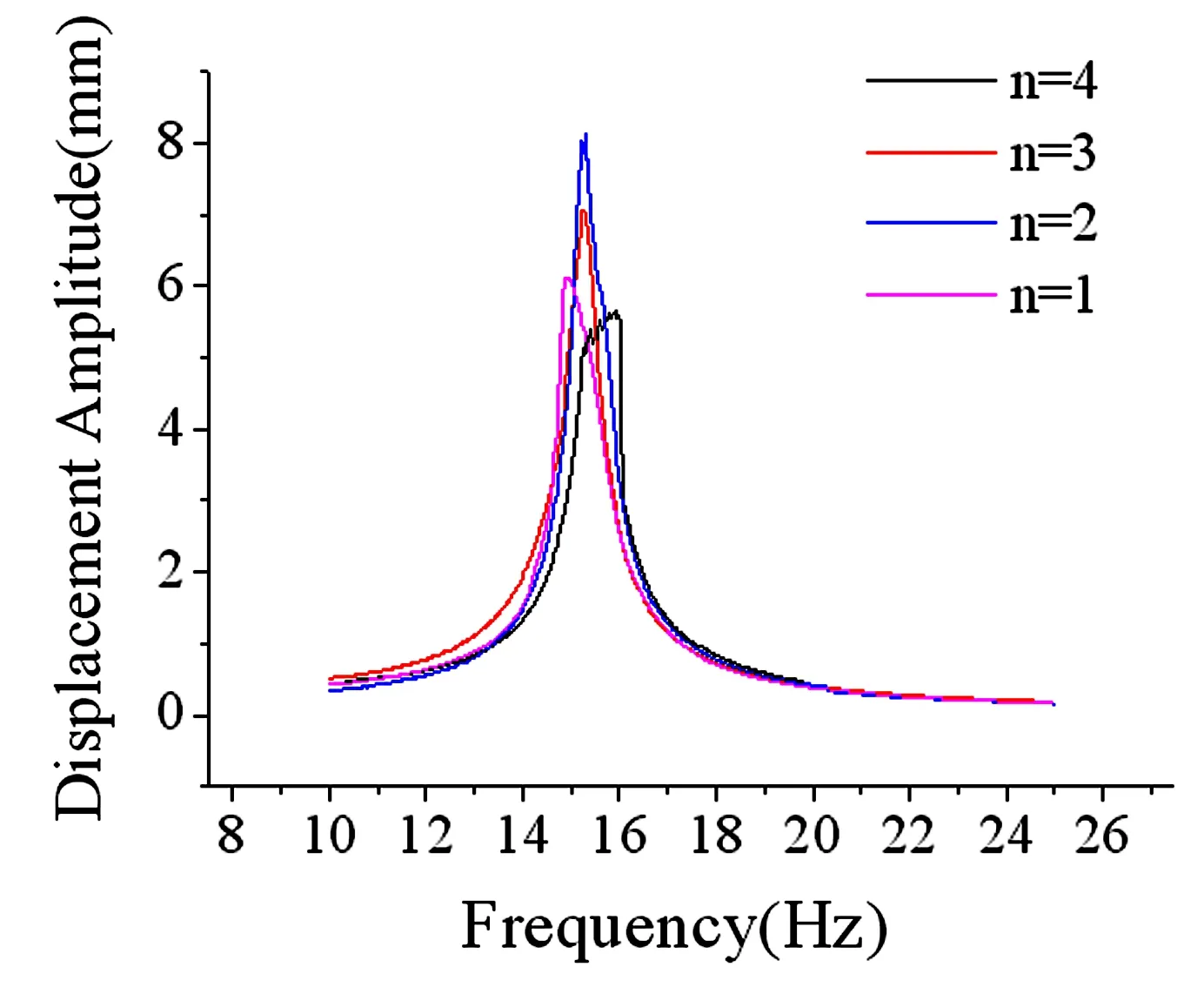
图8 改变间隙大小从低到高扫频位移频响曲线Fig.8 Frequency response curves when scanning from low to high frequency under different clearance distance

由图8实验结果所示,外激励0.4N时垫1片钢尺(间隙距离7.8mm)、垫2片钢尺(间隙距离7.1mm)、垫3片钢尺(间隙距离6.3mm),系统动态特性仍呈现线性系统,在垫4片钢尺(间隙距离4.7mm)时薄片梁与主梁发生碰撞,此时结构的等效接触刚度变大,实验曲线可以观察到位移频响曲线出现频率跳跃特征,结构呈现变硬的非线性特性.

F=0.8N——改变间隙宽度大小(1片钢尺间隙距离7.8mm—2片钢尺间隙距离7.1mm—3片钢尺间隙距离为6.3mm—4片钢尺间隙距离4.7mm),位移响应曲线如图9所示.

图9 改变间隙大小从低到高扫频位移频响曲线Fig.9 Frequency response curves when scanning from low to high frequency under different clearance distance

由图9实验结果可以得知,在外激励逐渐变大为0.8N时位移频响曲线出现频率跳跃的现象,此时主梁与薄片梁开始碰撞,接触刚度变大,结构呈现变硬的特性.

从以上实验结果图中不难发现,改变间隙距离大小与改变外激励幅值大小系统呈现相同的频响特性变化规律,即随着间隙距离减小,主梁与薄片梁发生碰撞,结构等效接触刚度变大,结构出现频率漂移的特征,随着间隙距离的减小系统动态特性由原来的线性系统转变为非线性系统.

3 双稳态实验现象的研究

3.1 跳跃区间变化规律

取薄片梁两端垫放钢尺片数4片(间隙距离为4.7mm),外激励幅值F从0.2N-0.4N-0.6N-0.8N-1.0N-1.2N-1.4N-1.6N-1.8N-2N逐渐变化,比较每一组外激励幅值高低、低高扫频曲线如图10所示.

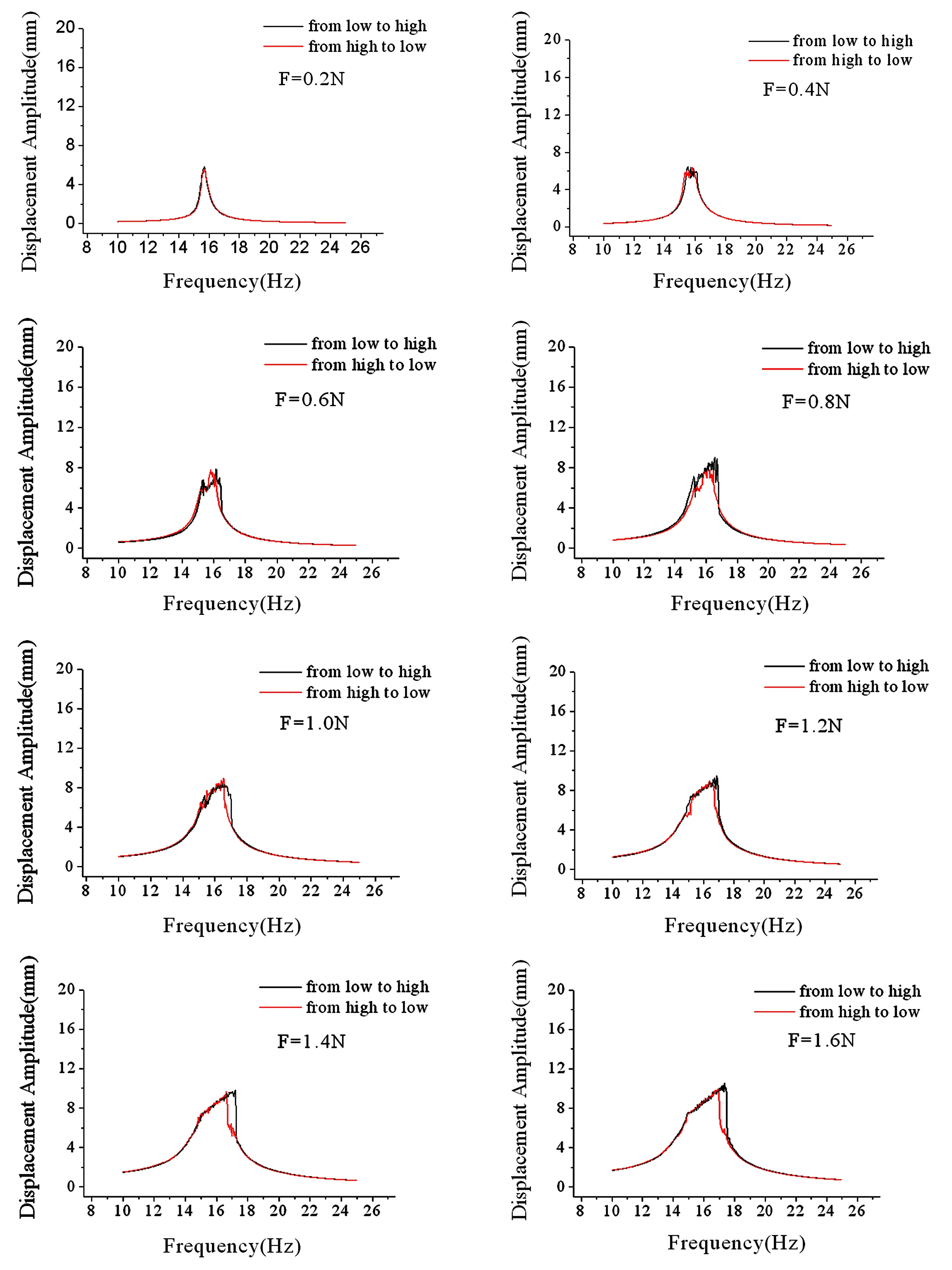
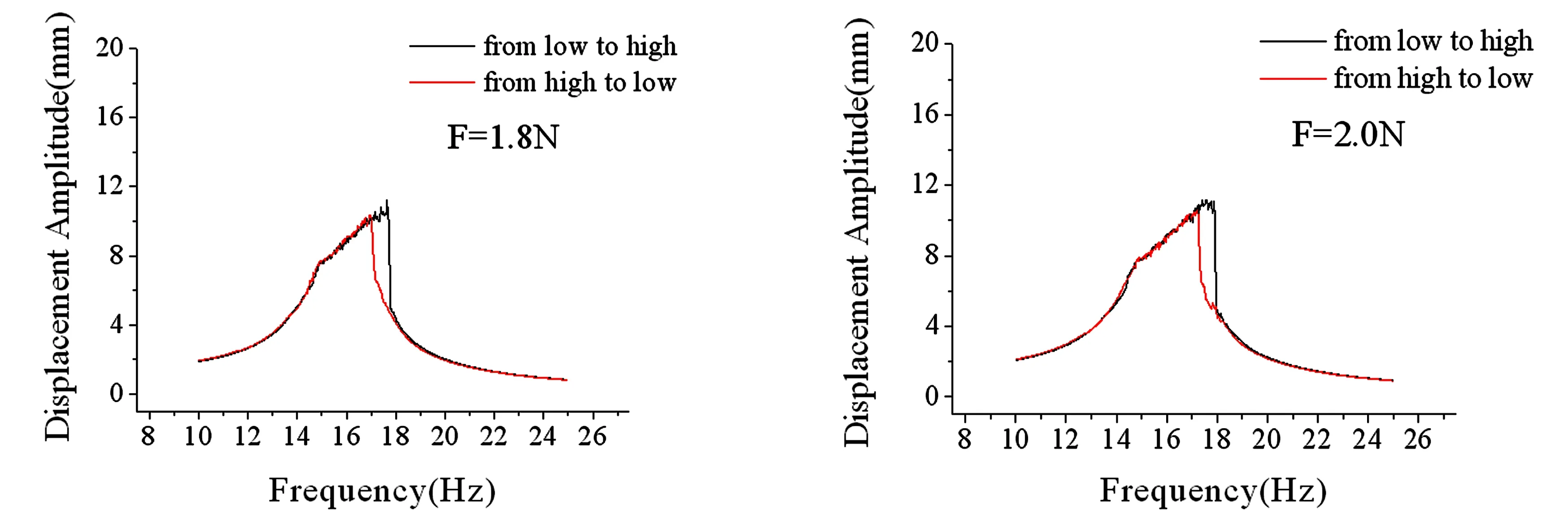
图10 不同外激励低高-高低扫频位移频响曲线Fig.10 Frequency response curves when scanning from low to high frequency with different force amplitude

实验结果的跳跃区间大小分别为表2所示.

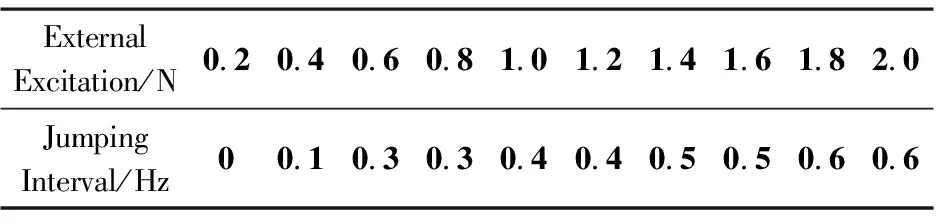
表2 不同激励力下跳跃区间大小Table 2 Jump range under different exciting force amplitude

结构在间隙距离为4.7mm,外激励幅值为0.6N发生碰撞,比较实验中从低到高扫频与从高到低扫频结构的位移频响曲线不难看出,跳跃区间随着外激励幅值的增大而逐渐增大,系统对应的特性由原有的线性系统逐渐转换为新的非线性系统,如表2所示.

3.2 双稳态特性研究

取一组薄片梁两端垫放钢尺片数为4片(间隙距离为4.7mm),外激励幅值大小为1.2N组合的工况研究时域曲线.分别在14Hz与16.9Hz进行定频激励,观察时域响应曲线.在定频激励过程中给予外激励敲击,观察时域曲线的稳态变化.实验曲线如图11所示.

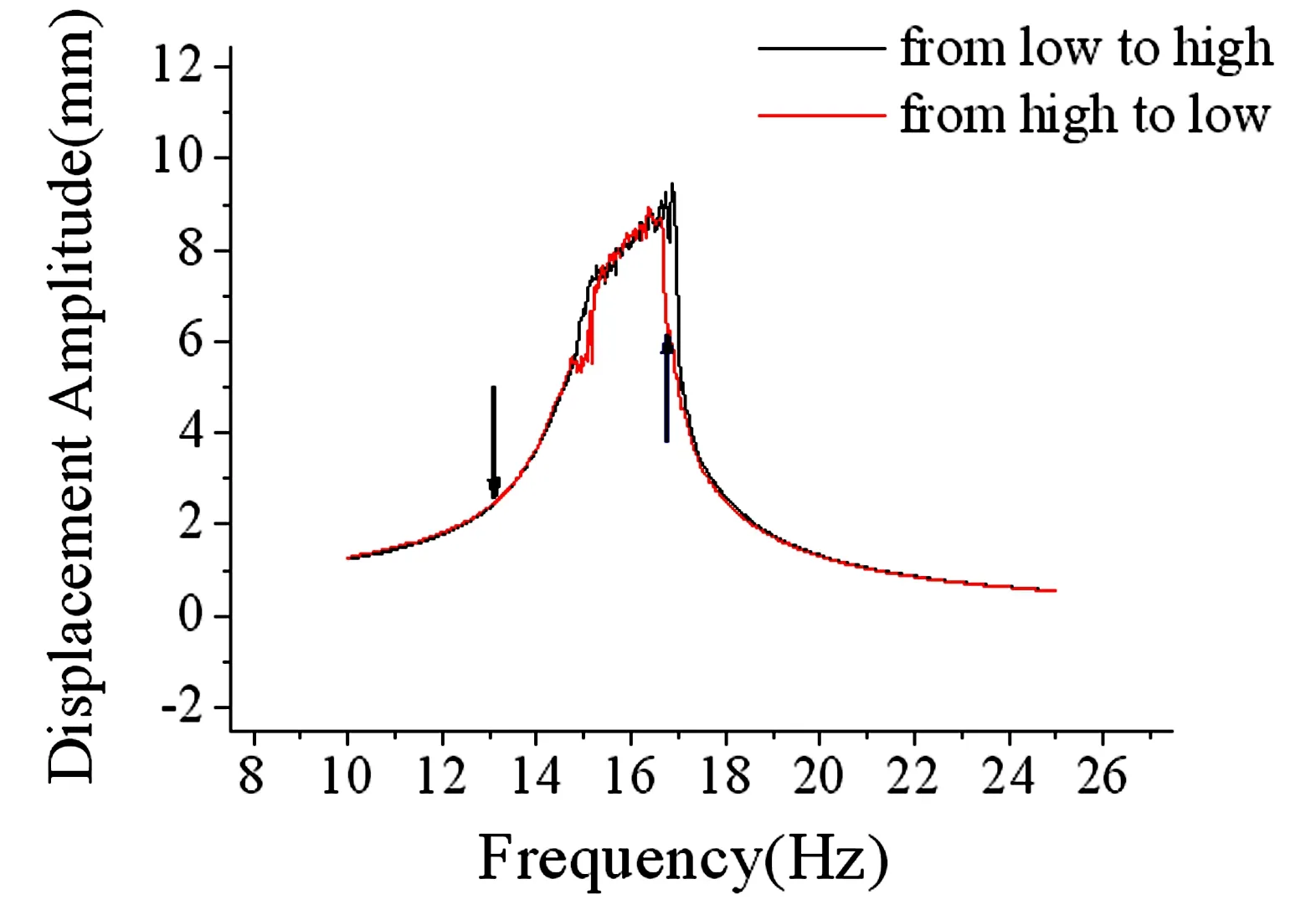
图11 外激励1.2N—垫4片钢尺低高-高低扫频位移频响曲线Fig.11 Frequency response curves when scanning from low to high and high to low frequency with n=4, F=1.2N

由时域曲线图12可以看出,在无跳跃区间14Hz对结构定频激励时只有一个稳态；在跳跃区间选取16.9Hz进行定频激励,结构出现了双稳态.

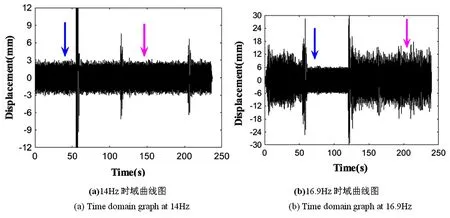
图12 时域位移响应曲线Fig.12 Displacement time domain response

分别取非跳跃点14Hz在30～40s(如图13(a))、150～160s(如图13(b))两个时间段做频谱分析；跳跃点16.9Hz时域曲线在70～80s(如图14(a))与200～210s(如图14(b))两个稳态下时域曲线做频谱分析.

图13 时域曲线频谱分析Fig.13 Curves of frequency spectrum analysis

由时域曲线图14做频谱分析可以看到,在非跳跃点14Hz结构只有一个频率成分,而在实验低高、高低扫频的位移频响曲线中可以观察到在结构频率跳跃点含间隙非线性梁结构出现多值解的典型非线性特征,在图14中时域曲线频谱分析图中也观察到在频率跳跃点16.9Hz结构出现连续倍频的运动学特征.

图14 时域曲线频谱分析Fig.14 Curves of frequency spectrum analysis

3.3 相曲线分析

对结构在跳跃点与非跳跃点运动的相曲线进一步分析,观察运动出现的特殊性.

非跳跃频率点14Hz的相曲线如图15所示,跳跃频率点16.9Hz的相曲线如图16所示.

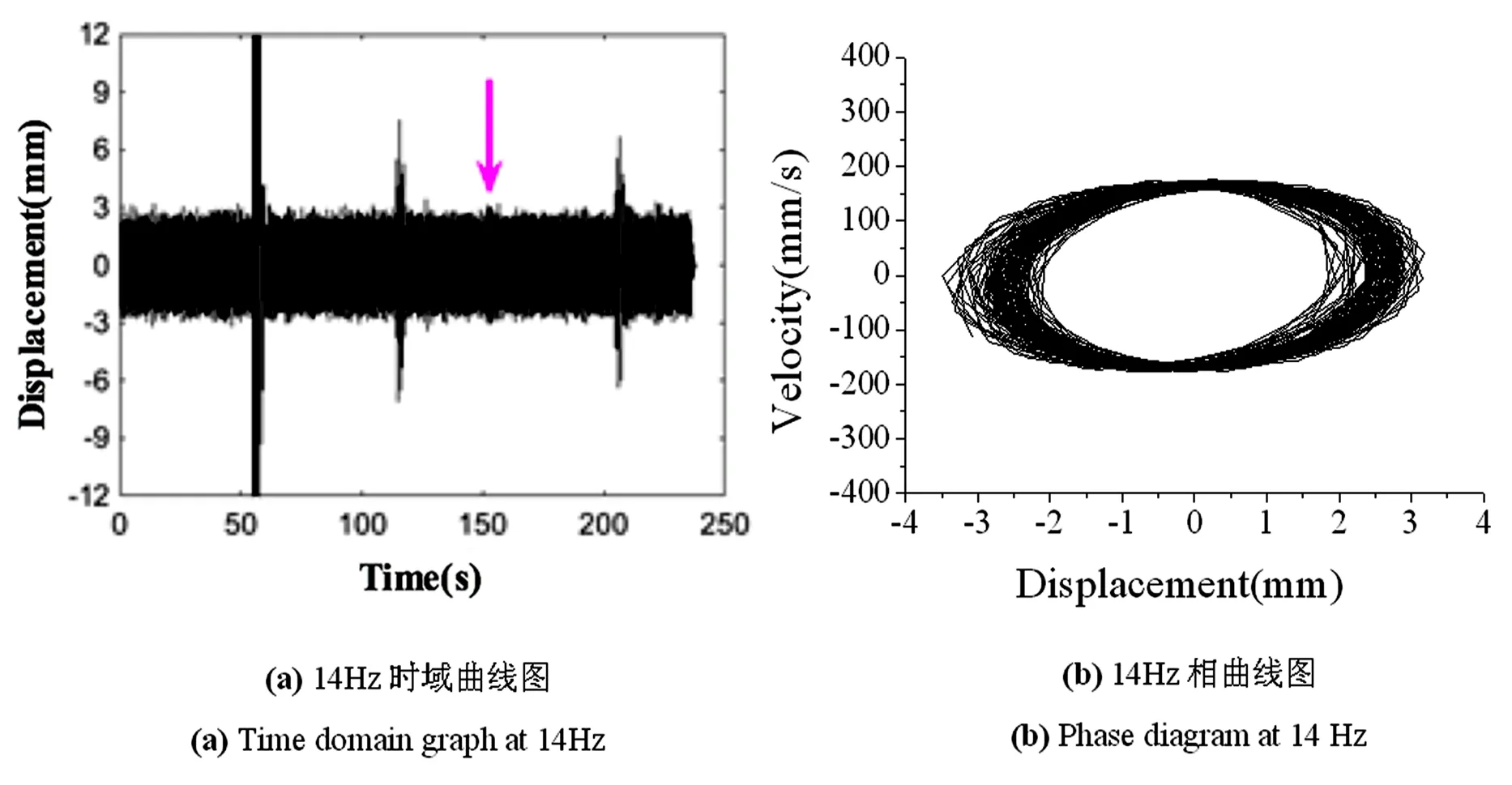
图15 非跳跃点14Hz相曲线分析Fig.15 Curves of the phase analysis for non jumping points at 14 Hz

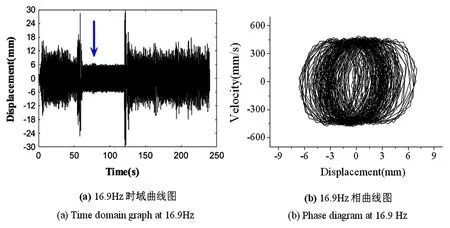
图16 跳跃点16.9Hz相曲线分析Fig.16 Curves of the phase analysis for jumping points at 16 Hz

由图15,图16相曲线可以看出,结构在非跳跃点14Hz处是一近似圆形的封闭曲线,而在跳跃点16.9Hz处200～210s处的相曲线呈现无序混乱的特征,两者具有明显的运动不同,跳跃点的混乱运动特性还需进一步研究理论分析加以证明.

4 仿真分析

为进一步阐明间隙宽度因素的影响机理,通过仿真计算进行对比.对研究结构的含单间隙限位结构的非线性部分,采用单自由度建模计算方法.计算中的物理参数以T字型梁的静力学和扫频实验测得的数据为基础,等效接触刚度k*=0.7N/mm,通过实验测量取平均值；采用等效质量0.1kg,比例阻尼c=1e-4,杨氏模量为2e11Pa,计算扫频范围f为10～20Hz,扫频间隔Δf=0.02Hz,得到该理论结果.

4.1 改变外激励幅值

间隙距离为垫4片钢尺(间隙距离大小4.7mm),外激励力幅值F的变化范围为0.2N-0.4N-0.6N-0.8N-1.0N-1.2N-1.4N-1.6N-1.8N-2.0N,主梁动力学响应,仿真与实验对比曲线如图17所示.

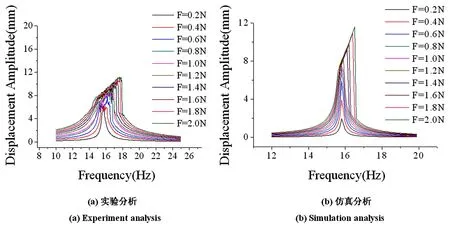
图17 改变外激励幅值实验—仿真对比Fig.17 Comparison of frequency response from experiment and simulation by changing the excitation amplitude

1)由仿真计算结果可以看出,含间隙非线性悬臂梁结构在间隙距离保持固定,随着外激励力的幅值增大,结构位移响应曲线第一阶频率逐渐增大,并且在外激励增大到一定值后出现了跳跃现象,与实验结果具有一致的规律,验证了实验的合理性.

2)仿真计算参数取实验测得的等效参数,在外激励力幅值为0.2N即实验中薄片梁还未与主梁发生碰撞,计算所得线性结构的第一阶频率与实验测得的线性结构固有频率相同,即f=15.8Hz.由实验测得曲线可以看到,在外激励力幅值F=0.4N时结构出现了变软的特性,由于在外激励幅值增大时主梁振动幅值增大,实验中主梁与薄片梁未发生碰撞,结构中包含立方非线性因素,使得结构的第一阶频率变小.随着外激励幅值的增大,主梁与薄片梁发生碰撞,等效接触刚度变大,位移频响曲线出现了频率跳跃现象.

3)由实验测得曲线可以看到,位移频响曲线在外激励力为0.6N时开始发生跳跃,而仿真计算在外激励幅值为1.0N开始出先跳跃现象,并且位移频响曲线幅值存在一定差异.本文采用的仿真计算忽略了重力、外激励冲击等因素对含间隙非线性结构的影响,且单自由度建模与实验结果在位移频响曲线的幅值大小存在一定误差.后续可通过优化仿真建模与实验结果进行进一步比对.

4.2 改变间隙宽度

外激励力幅值F为0.8N,间隙宽度为悬臂梁—垫1片钢尺间隙距离为7.8mm(仿真间隙距离为7.8mm)—垫2片钢尺间隙距离7.1mm(仿真间隙距离为7.1mm)—垫3片钢尺间隙距离为6.3mm(仿真间隙距离为5.3mm)—垫4片钢尺间隙距离为4.7mm(仿真间隙距离为4.5mm)的间隙距离改变时主梁动力学响应仿真与实验对比如图18所示.

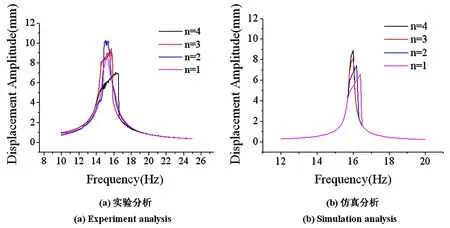
图18 改变间隙距离大小实验—仿真对比Fig.18 Comparison of frequency response from experiment and simulation by changing the clearance distance

1)由仿真计算结果可以看出,含间隙非线性悬臂梁结构外激励力幅值保持一定,随着间隙距离的逐渐减小,结构位移响应曲线第一阶频率逐渐增大,并且在间隙距离达到一定值后出现了频率跳跃现象,结构变硬的特性,与实验结果具有一致的规律,验证了实验的合理性.

2)由实验位移频响曲线与仿真位移频响曲线对比可以看到,在垫1片钢尺间隙距离为7.8mm和垫2片钢尺间隙距离为7.1mm时,结构的主梁与片梁未发生碰撞,结构为线性结构第一阶固有频率f=15.8Hz.在垫3片钢尺间隙距离减小为6.3mm时主梁与片梁发生碰撞,结构的等效接触刚度变大,位移频响曲线出现了频率跳跃现象,结构变硬的特性.

3)由于实验中碰撞过程含有冲击等因素,本文采用的仿真计算中忽略了外激励冲击、重力等因素对含间隙非线性结构的影响,且单自由度建模的方法与实验结构的测量结果在位移频响曲线的幅值大小存在有一定误差.后续可通过优化仿真建模与实验结果进行进一步比对.

5 结论

本文主要采用实验方法研究了改变外激励力幅值从低频到高频与从高频到低频扫频曲线对含间隙非线性梁结构位移频响特征的影响,但受到实验仪器与实验时长的约束,难以通过无限缩小扫频频率间隔或对其他参数进行大范围试验来捕捉任意跳跃区间.因此需要在实验前确定较优的实验设置参数,使得结构在该参数下出现明显的跳跃特征.

研究结果表明：

1)含间隙非线性梁结构的非线性因素受两种参数影响,随着外激励力幅值的不断增加,结构发生碰撞等效刚度变大,跳跃频率点变大,结构出现了明显的变硬特性；随着间隙距离大小的减小,含间隙限位非线性梁结构跳跃频率不断增大,结构同样出现变硬特性.

2)随着外激励幅值的增大,含间隙限位非线性梁低高-高低扫频,位移频响曲线出现明显的跳跃现象,所得频响曲线的跳跃规律为：随着外激励的增大,跳跃区间的大小逐渐增大而趋于饱和状态,含间隙限位非线性结构的频响特性也呈现了线性状态—出现非线性状态—非线性达到最强的变化规律.

3)通过实验观测到在不稳定跳跃区间频率点的定频激励下,结构的时域响应具有多稳态现象,在双稳态时域响应曲线中选取不同稳态的时间段做频谱分析,均有连续倍频的动力学行为.

实验从宏观上揭示并总结了间隙距离大小,外激励幅值大小两种参数的变化对含间隙非线性梁结构位移频响之间的变化规律,仿真计算结果说明了实验结果的合理性.对含间隙非线性悬臂梁在影响参数设计方面具有重要的应用价值,为后续的理论研究和仿真建模参数设计提供一定的指导.

1Foster C L, Tinker M L, Nurre G S, et al. Solar-array-induced disturbance of Hubble space telescope pointing system.JournalofSpacecraftandRockets,1995,32(4):634～644

2阎绍泽. 航天器中含间隙机构非线性动力学问题及其研究进展. 动力学与控制学报,2004(2):50～54(Yan S Z. Development and problems of nonlinear dynamics of the mechanisms with clearances for space-crafts.JournalofDynamicsandControl,2004(2):50～54(in Chinese))

3王珺,赵环迪,陈力奋. 预变形对非线性结构响应特征的影响. 动力学与控制学报,2015,13(3):188～193(Wang J, Zhao H D, Chen L F. Effects of the initial deformation on the dynamic response of local nonlinear systems.JournalofDynamicsandControl,2015,13(3):188～193(in Chinese))

4赵环迪,王珺,陈力奋. 含非线性边界梁结构频响特征的实验研究. 振动与冲击,2015,34(4):82～89(Zhao H D,W ang J, Chen L F. Test for frequency response features of a beam structure under nonlinear boundaries.JournalofVibrationandShock,2015,34(4):82～89(in Chinese))

5Arslan Ö, Aykan M, Özgüven H N. Parametric identification of structural nonlinearities from measured frequency response data.MechanicalSystemsandSignalProcessing,2011,25:1112～1125

6Özer M B, Özgüvenb H N, Royston T J. Identification structural non-linearities using describing functions and the Sherman-Morrison method.MechanicalSystemsandSignalProcessing,2009,23:30～44

7颜科鹏,陈力奋. 含非线性柔性约束梁结构的多稳态响应实验研究. 复旦学报,2015(3):356～364(Yan K P, Chen L F. Experimental study of multi-stable vibration characteristics of nonlinear beams with flexible constraints.JournalofFudanUniversity,2015(3):356～364(in Chinese))

8阎绍泽,向吴维凯,黄铁球. 计及间隙的运动副和机械系统动力学的研究进展. 北京大学学报,2016,52(4):741～755(Yan S Z, Xiang W W K, Huang T Q. Advances in modeling of clearance joints and dynamics of mechanical systems with clearances.ActaScientiarumNaturaliumUniversitatisPekinensis,2016,52(4):741～755(in Chinese))

9张晨旭,杨晓东,张伟. 含间隙齿轮传动系统的非线性动力学特性的研究. 动力学与控制学报,2016,14(2):115～121(Zhang C X, Yang X D, Zhang W. Study on non-linear dynamics of gear transmission system with clearance.JournalofDynamicsandControl,2016,14(2):115～121(in Chinese))

10Han R P S, Luo A C J. Chaotic motion of a horizontal impact pair.JournalofSoundandVibration,1995,181(2):231～250

11Yoshitake Y, Sueoka A, Shoji N, et al. Vibrations of nonlinear systems with discontinuities.TheJapanSocietyofMechanicalEngineers,1998,41(4):710～717

12陈思雨,唐进元,谢耀东. 齿轮传动系统的非线性冲击动力学行为分析. 振动与冲击,2009,28(4):70～75(Chen S Y, Tang J Y, Xie Y D. Analysis of nonlinear impact dynamic behavior for a gear pair system with time varying stiffness and friction.JournalofVibrationandShock,2009,28(4):70～75(in Chinese))

13阎绍泽,陈鹿民,吴德隆等. 空间可展结构非线性动力学特性实验研究. 宇航学报,2002(4):1～3(Yan S Z, Chen L M, Wu D L, et al. Experimental study on nonlinear dynamic characteristics of spatial deployable structures.JournalofAstronautics,2002(4):1～3(in Chinese))

14Blankenship W, Kahraman A. Steady state forced response of a mechanical oscillator with combined parametric excitation and clearance type nonlinearity.SoundVibration,1995,185:743～765

15曹妍妍,赵登峰. 间隙约束悬臂梁系统的动力学行为实验研究. 振动与冲击,2007,26(4):154～157(Cao Y Y, Zhao D F. Experimental study on dynamic behavior of cantilever beam system with gap constraint.JournalofVibrationandShock,2007,26(4):154～157(in Chinese))

16Praveen Krishna I R, Padmanabhan C. Experimental and numerical investigations of impacting cantilever beams part1: first- mode response.NonlinearDynamics,2012,67(3):1985～2000

17孙东阳,陈国平,王铁成. 谐波齿轮传动的含间隙机构的动力学分析. 振动与冲击,2014,33(23):160～164(Sun D Y, Chen G P, Wang T C. Dynamic analysis of a mechanism with clearances and harmonic gear transmission.JournalofVibrationandShock,2014,33(23):160～164(in Chinese))

18谷勇霞,杨天夫,郭峰. 考虑多间隙的帆板式展开机构动力学分析. 振动、测试与诊断,2015,35(1):36～41(Guo Y X, Yang T F, Guo F. Dynamic performance of a solar array deployable mechanism with multiple clearances.JournalofVibration,Measurement&Diagnosis,2015,35(1):36～41(in Chinese))

19胡世武,郭杏林. 含双间隙连杆机构动力学仿真与实验. 计算力学学报,2015,32(4):548～553(Hu S W, Guo X L. Dynamic simulation and experiment of a linkage mechanism with double clearances.ChineseJournalofComputationalMechanics,2015,32(4):548～553(in Chinese))