船载三轴天线极化稳定技术研究

2018-07-06耿大孝张振庄

无线电通信技术 2018年4期

耿大孝,张振庄,刘昕

(中国电子科技集团公司第五十四研究所，河北石家庄 050081)

0 引言

国内在Ku、C等频段的卫星通信的极化方式主要是线极化方式，信号载波通过水平、垂直两种相互正交的极化实现极化隔离[1]。随着我国卫星覆盖区域由陆地近海向深海远洋扩展，船载卫通站越来越多地需要采用国内线极化卫星作为中继站构建远程通信网络，作为通信终端的船载天线需要具有跟踪线极化卫星的能力。由于船体姿态角既影响天线电轴的空间指向，也对天线电轴形成旋转效应，造成极化失配。较大的极化失配角会增大极化损耗，降低交叉极化隔离度，和同频反极化信号构成收发相互干扰。为此船载卫通天线需要隔离船体姿态对天线极化的影响，保持天线地理极化角的稳定。

由于过去船载卫通天线跟踪只关注天线电轴相对目标卫星的指向误差，对极化稳定情况关注很少，一般不提供精度较高的实时摇摆角，因此过去船载卫通天线不采取极化稳定措施，只在两轴座架的机载卫通天线上考虑到飞机转弯时滚转角较大，进行了机体摇摆角到天线电轴的扰动量计算和隔离[2]，但由于扰动量没有与极化角相对应，因此存在一定的计算误差。

方位-俯仰-交叉式(即AEC)三轴座架因其可以实现高仰角过顶跟踪同步卫星，是船载卫星通信天线常用的座架形式。本文结合机载两轴座架极化摇摆扰动量计算公式，在船载三轴卫通天线上，综合天线地理角、船体姿态角、天线甲板角，通过坐标旋转变换，推导出对应于指定地理极化角的目标极化角计算公式，进而开发出船载天线极化稳定方法。

1 极化稳定方法研究

极化是指电磁波在传播过程中电场矢量的方向，若电场矢量在与电磁波传播方向垂直的平面内,则是线极化。地球同步卫星电场矢量方向与赤道平面平行时为水平极化，垂直时为垂直极化[3]。极化角一般是指水平极化角，在天线所在的地理平面内，同天线指向目标卫星的射线垂直的直线与赤道平面的夹角就称为极化角，计算公式见下式。

θp=arctan(sinΔλ/tanφ)，

(1)

式中，θp为极化角，Δλ为地球卫通站与卫星经度差，φ为天线纬度[4]。由式可知，极化角的数值只与地球站的经纬度、卫星的经度等因素有关。船载天线极化稳定的目的就是隔离船体姿态角对船载天线极化角的影响。

船载天线极化稳定方法研究的主要工作是推导出船摇条件下的目标极化角计算公式，本文应用欧拉旋转方法按照惯性(地理)坐标系—甲板坐标系—天线坐标系的顺序，结合地理角、姿态角、甲板角等各坐标系的特征值进行坐标旋转，得出矩阵转换等式，从而求出天线目标极化角。

1.1 坐标系

船摇对天线极化的扰动计算公式是通过各定位坐标系的旋转推导求得，涉及到的坐标系说明如下[2]。

① 惯性(地理)坐标系(Og—XgYgZg)

原点Og在惯导基准中心，Xg轴平行于水平面指向正东，Yg轴平行于水平面指向正北，Zg轴铅垂向上，Og—XgYgZg成右手正交坐标系。

② 甲板(船体)坐标系(Od—XdYdZd)

原点Od在船体质心，Xd轴平行于甲板平面指向右舷，Yd轴平行于甲板平面指向船艏，Zd轴垂直于甲板平面指向船桅，Od—XdYdZd成右手正交坐标系。

③ 天线坐标系(Oa—XaYaZa)

原点Oa在天线质心，天线质心与船体质心重合，Ya轴与天线电轴重合，Za轴平行于交叉轴并指向天线主面的上边沿，Xa轴垂直于交叉轴与电轴构成的平面，Oa—XaYaZa成右手正交坐标系。

1.2 数学模型建立

船摇对天线极化扰动的推导是建立在天线对星指向转动到位并且已经锁定目标卫星的基础上，忽略天线对星指向偏差，计算基于地理角、船摇角和天线座架各轴角得出的目标极化角，推导过程是天线的单位向量按照天线坐标系—惯性坐标系—甲板坐标系—天线坐标系的顺序欧拉旋转推导。

坐标正向转换坐标轴的旋转顺序为Z轴—X轴—Y轴，反向转换旋转顺序为Y轴—X轴—Z轴。

设天线矢量在天线坐标系中的表示为式(2)，因为只分析极化角变化，所以假设只有Z轴方向有单位矢量。

(2)

由天线坐标系欧拉旋转到惯性坐标系，转换参数为天线指向的方位地理角、俯仰地理角和极化地理角，表示为A、E、P，坐标{X，Y，Z}先逆转P角到坐标{X1，Y1，Z1}，再下转E角到坐标{X2，Y2，Z2}，再逆转A角到坐标{X3，Y3，Z3}，转换过程如图1所示。

图1 天线坐标到地理坐标转换示意图

极化地理角旋转矩阵如式(3a)所示:

(3a)

俯仰地理角旋转矩阵如式(3b)所示:

(3b)

方位地理角旋转矩阵如式(3c)所示:

(3c)

由惯导坐标系转换到甲板坐标系，转换的旋转示意如图2所示。

图2 惯导坐标到甲板坐标转换示意图

转换参数主要是航向、纵摇、横摇三个姿态角，表示为k、p、r，转换顺序按照航向—纵摇—横摇的顺序。各矩阵说明如下:

航向转换矩阵如式(4a)所示:

(4a)

纵摇转换矩阵如式(4b)所示:

(4b)

横摇转换矩阵如式(4c)所示:

(4c)

甲板坐标转换至天线坐标，转换示意如图3所示。

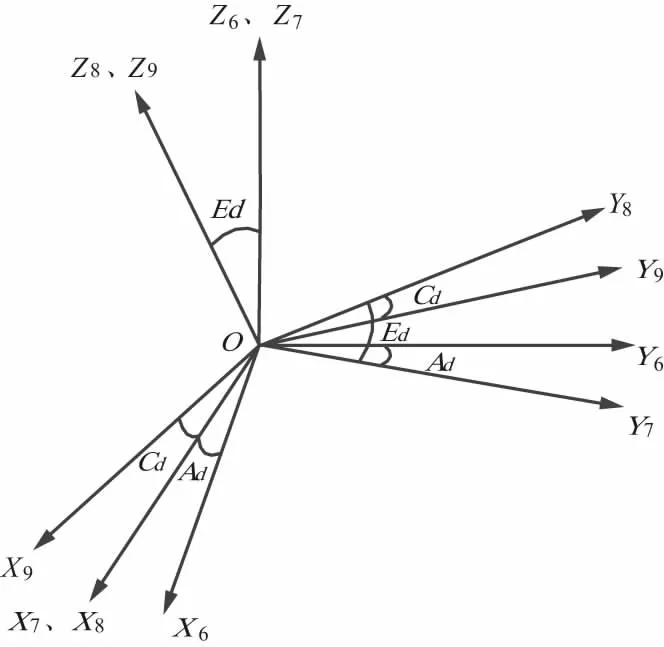
图3 甲板坐标到天线坐标转换示意图

转换参数主要是方位、俯仰、交叉三个甲板角，表示为Ad、Ed、Cd，转换顺序按照方位—俯仰—交叉甲板角的顺序来旋转。各矩阵说明如下。

方位甲板角转换矩阵如式(5a)所示:

(5a)

俯仰甲板角转换矩阵如式(5b)所示:

(5b)

交叉甲板角转换矩阵如式(5c)所示:

(5c)

1.3 极化目标甲板角计算

设通过天线对星指向的矢量在各坐标系的顺序转换即可得到极化轴变量的最终结果。

将转换过程中用到的转换矩阵相乘[5]，得矩阵等式如式(6a)所示:

(6a)

式中，X9为电轴在天线坐标系中Xa轴轴向的分量，Z9为电轴在Za轴轴向的分量，矩阵加上标T后为各矩阵的转置矩阵。

设经船体姿态引出的目标极化角为Pd，Pd计算式为(6b):

Pd=arctan(X9/Z9)。

(6b)

1.4 极化稳定实现

船载卫通天线在对星跟踪过程中，控制极化轴，使实测的实际极化角与实时计算的目标极化角保持一致，即可隔离船摇对天线极化的扰动，实现极化稳定功能。

2 应用分析

2.1 仿真计算

① 特征值计算

当俯仰地理角E= 90°，横纵摇角和交叉甲板角为零，俯仰甲板角Ed=90°时，得出目标极化角Pd=P+A-k-Ad，即当天线位于星下点，船甲板水平状态下，方位的剩余误差只体现在对极化的扰动上；当只有横摇角，其他旋转变量都为零时，得出极化甲板目标角Pd=P-r，横滚角造成了极化旋转。

② 静态验证

将1.2 m Ku频段船载三轴天线安装在三轴摇摆台上，由惯导提供摇摆台的摇摆角。在天线完全对准线极化卫星状态下，手动调整极化角使频谱仪检测到的反极化信号的强度最小，将调整后的实测极化角与目标极化角进行比较。改变摇摆台姿态并重复前面的过程，以此来验证公式的正确性，试验用星信息如表1所示。

表1 试验用星表

参数名称参数值卫星名称亚太Ⅵ号星经位置东经,134°工作频段C频段极化及信标垂直,3.7 GHz 参数名称参数值反极化信标水平,4 199.825 MHz天线经度东经114.43°天线纬度北纬38.04°天线对星角A:150.1°E:41.4°P:66.8°

试验中记录了五组姿态角对应的天线各轴甲板角，记录如表2所示。

表2 试验记录表(单位为°)

序号航向纵摇横摇方位甲板角俯仰甲板角交叉甲板角实测极化角目标极化角1204.7-8.9-15.7305.459.32.261.560.72197.66.5-24.2312.553.114.6-85.6-86.23179.821.7-21.5330.329.913.9-77.3-78.14162.324.1-6.5347.818.74.581.180.65155.315.88.9354.824.73.043.843.1

极化实测角与极化计算角虽然存在一定的误差，考虑到极化角的标校误差和信号电平的测量误差，该误差基本可以忽略不计，因此认为该方法起到了极化稳定的作用。

③ 动态验证

通过摇摆台动态摇摆试验，在天线伺服系统中进行有无极化稳定功能的反极化信号接收幅度的比较，确定在动态摇摆条件下，极化稳定隔离的效果。

船载天线在摇摆台持续摇摆条件下对星实时跟踪，采集天线应用极化稳定方法前后两个时间段接收信号的电平值，绘制成图形进行比较，从而确定在动态摇摆条件下极化稳定方法是否有效。

摇摆状态下天线未采用极化稳定方法信标信号的电平变化如图4所示。

图4 极化未稳定的信标电平图

同一摇摆状态下天线采用极化稳定方法后的信标信号的电平变化如图5所示。

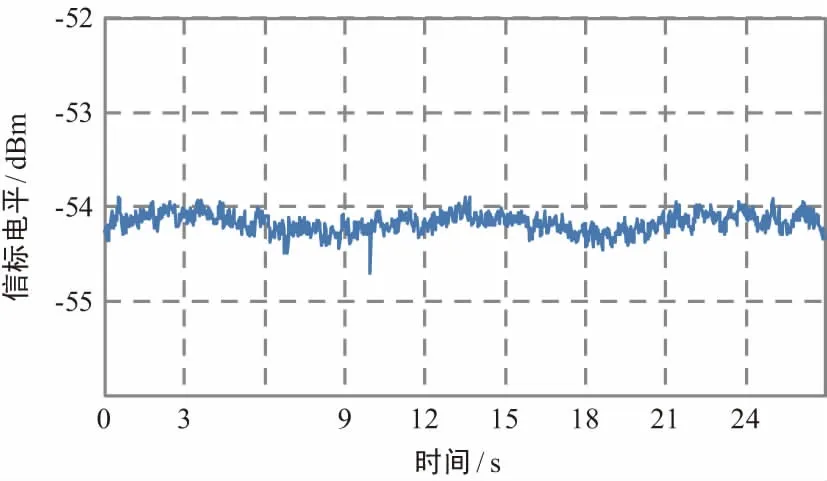
图5 极化稳定后的信标电平

比较图4和图5表示的信标电平变化示意图可见，两图都表现出了和摇摆同周期的变化，但加入极化稳定后的信标电平明显比极化稳定前平稳。

2.2 实际应用

一艘航天测量船船载卫通天线采用AEC座架，在执行某次卫星发射任务的航渡期间，船载卫通天线跟踪线极化卫星。船在星下点附近过赤道，卫通天线仰角较高，在没有采取极化扰动隔离时，天线收发信号出现较大跌落，通信偶有中断现象。

后来在伺服控制程序中依据该方法增加了极化稳定措施，在同一位置附近跟踪同样卫星，天线收发信号没有出现明显变化，从而判断该措施有效地解决了问题。

3 结束语

通过坐标旋转推导出目标极化角的计算公式，实现了天线对星极化在船摇条件下的稳定，避免了船体摇摆对船载卫通天线造成的极化干扰。目前，该极化稳定方法已应用于不同频段和口径的AEC座架的船载卫星通信天线中，而且都取得了很好的效果。同时通过坐标旋转推导目标极化角计算公式的研究方法不仅适用于AEC三轴座架天线，还可以推广应用在其他座架形式天线的极化稳定研究中。

[1] 王秉钧，王少勇，田宝玉.现代卫星通信系统[M].北京:电子工业出版社.

[2] 李华.机载卫星通信天线极化轴的稳定分析[J].现代电子技术,2002(11)：47-48.

[3] 张印相.卫星直播数字电视[M].北京:中国标准出版社，2011.

[4] 林培通.卫星接收极化角计算公式的推导[J].宁德师专学报(自然科学版),2004,16(4)：400-402.

[5] 张凯院，徐仲.矩阵论[M].北京:科学技术出版社,2013.

[6] 蔡国新,张滨,伍宗伟,等.关于极化角计算的研究[J].无线电通信技术，2009，35(5)：37-38.

[7] 梁国,王建.一种共形天线阵支架的结构设计与仿真分析[J].无线电通信技术,2016,42(1):65-68.

[8] 王道平,陈辉华,何敏.“动中通”接收天线极化匹配及跟踪技术研究[J].现代电子技术,2009(12)：103-105.

[9] 徐崇彦,张言锋,孟祥国.Ka频段低轨卫星跟踪技术研究[J].无线电通信技术,2017,43(6):56-59.

[10] 马利华，胡超，毛新宏，等.卫星通信地球站天线的线极化角计算研究[J].天文研究与技术，2016，13(4)：428-432.

[11] 单福悦,凡嵩,岳建,等.基于多波束阵列天线的目标快速捕获方法[J].无线电工程,2016,46(4):60-62.

[12] 杜彪,伍洋,张一凡,等.大口径反射面天线技术综述[J].无线电通信技术,2016,42(1):1-8.