无线传感器网络下GFDM信号检测技术研究
2018-07-06任文成
任文成
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
认知无线传感器网络(WSN)通过检测“频谱空穴”和机会频谱接入方法充分利用频谱,解决了WSN频谱资源有限和固定频谱分配而导致频谱使用效率低的问题[1-2]。广义多载波传输技术(GFDM)采用低旁瓣的非矩形信号作为成形脉冲,降低了带外功率泄露,GFDM只需对一帧符号添加循环前缀,不必在每一个符号前面添加循环前缀,在避免了帧间干扰的同时提高了频谱利用率[3],而且GFDM调制可有效利用离散频域资源,以上特点使GFDM调制可用作认知无线传感器网络的底层传输技术。
然而GFDM调制各子载波不再保持正交性,将会引入子载波间干扰(ICI)[4],增加接收端算法的复杂度。文献[5]提出了干扰抵消类算法,在加性白高斯噪声信道(AWGN)下误码率与OFDM系统相似。本文研究在认知无线电传感器网络频率选择性信道环境下的GFDM信号检测算法,并比较了迫零、匹配接收以及双边干扰抵消算法的性能。
1 GFDM信号的产生
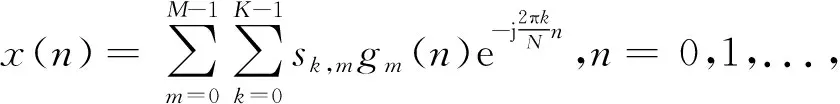

图1 GFDM系统发射机框图
原型脉冲g(n)对于GFDM系统的抗符号间干扰和抗子载波间干扰性能至关重要。在GFDM系统中,第m个时隙的成形脉冲波形gm(n)由原型脉冲经过循环移位mN个数据形成,即:gm(n)=g(
图2给出了连续三个时隙内的时域脉冲波形,N=24,采用升降因子为0.5的根升余弦脉冲。图3为相邻三个信道的子载波频谱,相对于矩形脉冲高达-13 dB的旁瓣功率,此时脉冲旁瓣功率仅为-40 dB,意味着传输波形对多普勒频移和频偏更具鲁棒性,但不足之处在于子载波间的频谱丧失了正交性,自身引入了ICI干扰,增加了算法的复杂度。

图2 连续三个时隙时域脉冲波形

图3 相邻子载波信号频谱
为了便于叙述,将发射信号改写为矩阵形式:x=AS,其中矩阵A∈CKM×NM包含了一帧中所有发送符号对应的循环移位脉冲波形。
2 GFDM信号的3种检测算法
2.1 迫零检测算法
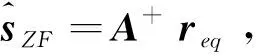
2.2 匹配滤波检测算法

图4 匹配滤波算法框图
与迫零检测算法相反,匹配滤波检测算法假设接收信号中只存在加性白高斯噪声,忽视信道引入的多径干扰。匹配滤波算法力图使检测后的输出信号中的信噪比(SNR)最大化。由于该算法完全忽视了信道多径干扰信号的存在,致使该算法对干扰信号非常敏感,恶化了信干噪比(SINR)指标,进而恶化误码率(BER)。
2.3 双边干扰抵消(DS-SIC)算法


图5 双边干扰抵消算法框图
双边干扰抵消算法结合了串行干扰抵消和匹配滤波算法,在克服了匹配滤波算法中不能消除信道噪声的缺点的同时,利用串行干扰抵消的策略最大化了检测后的信噪比。
3 仿真结果及分析
仿真采用64路子载波,每帧包括3个时隙,上采样因子64,时隙长度256 μs,子载波间隔3 906 Hz,QPSK调制形式,脉冲成形波形为升降因子为0.5的根升余弦脉冲。采用两种六径信道模型,信道A相干带宽为11.97 kHz,时延为0、2 μs、3 μs、4 μs、7 μs、11 μs,增益为0 dB、-7 dB、-6 dB、-22 dB、-16 dB、-20 dB;信道B相干带宽为7.23 kHz,时延为0、3 μs、8 μs、11 μs、13 μs、21 μs,增益为0 dB、-7 dB、-15 dB、-22 dB、-24 dB、-19 dB。
图6~图8显示了3种GFDM信号检测在3种不同信道环境下的误符号率。其中OFDM检测采用最小均方误差检测算法。在3种信道环境中,匹配滤波算法忽视了干扰信号,其性能都是最差的。迫零算法的性能和双边干扰抵消算法的性能近似,但是迫零算法由于需要求矩阵伪逆,复杂度远高于双边干扰抵消算法,但是后者的计算时延要比迫零算法大。同时还应注意到,在3种信道环境下,基于双边干扰检测算法的GFDM系统性能非常接近于没有子载波间干扰存在情况下的OFDM系统性能,但是GFDM系统的频谱效率,带外功率泄露远优于OFDM系统。
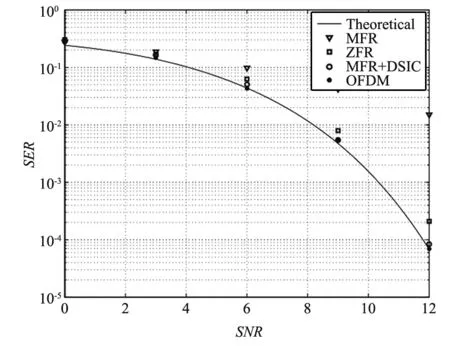
图6 AWGN信道下GFDM和OFDM性能
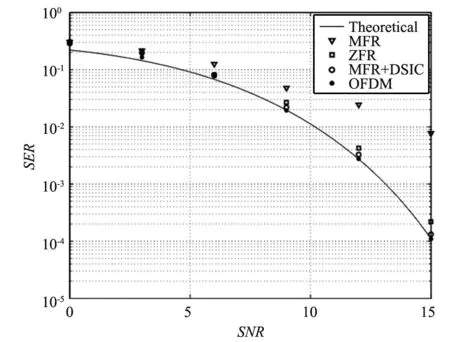
图7 信道A下的GFDM和OFDM性能
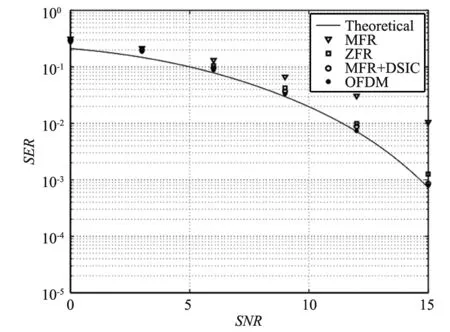
图8 信道B下的GFDM和OFDM性能
4 结束语
广义频分复用(GFDM)调制解调技术由于具有较小的带外功率泄露,能够适用于离散的可用频谱环境中,较OFDM系统更加适合于认知无线传感器网络应用,在未来无线通信网络中会占有一席之地。对于频率选择性衰落信道环境下GFDM信号的检测方案,基于双边干扰抵消的GFDM检测算法在保留GFDM带外功率泄漏小、频谱利用率高等优点的基础上,误码率性能优于迫零算法和匹配滤波检测算法,接近于OFDM系统的误码率性能,而且算法的复杂度较低,利于后期工程实现。
[1] Mitola J.Cognitive Radio for Flexible Mobile Multimedia Communications[C]∥ Mobile Multimedia Communications,1999.(MoMuC '99) 1999 IEEE International Workshop on.IEEE,2002:435-441.
[2] 邵敏斯,毛建旭,黄晓霞.基于智能天线的认知无线电网络频谱访问协议[J].传感器与微系统,2012,31(10):70-74.
[3] Michailow N,Gaspar I,Krone S,et al.Generalized Frequency Division Multiplexing:Analysis of an Alternative Multi-carrier Technique for Next Generation Cellular Systems[C]∥ International Symposium on Wireless Communication Systems.IEEE,2012:171-175.
[4] Proakis J G.数字通信[M].4版.北京:电子工业出版社,2003.
[5] Michailow N.Intergration of a GFDM Secondary System in an Existing OFDM System[D].Germany,Dresden:Technische Universitat Dresden,2010.
[6] 赵辰,刘应状,朱光喜.VLST系统中ZF检测算法的研究[J].无线电通信技术,2007,33(2) :37-39.
[7] 高凌翔.MIMO系统中检测方法的研究及其改进[J].无线电通信技术,2007,31(5) :9-11.
[8] 钟杏梅,蔡国权,牛忠霞.色散CDMA信道中基于子空间的盲多用户检测[J].无线电通信技术,2007,27(2):30-34.
[9] 李峰,潘申富,陆建平.串行干扰抵消器性能分析[J].无线电工程,2005,35(5) :1-2,35.
[10] 王永民,苟彦新,孟相如.基于干扰抵消的多用户检测[J].无线电通信技术,2004,30(4) :8-10.
[11] 李红军,蒋佳,葛建华,等.一种低复杂度STBC译码算法[J]无线电通信技术,2007,33(4) :31-33,56.
[12] 刘萍,胡捍英,于宏毅,等.第三代移动通信中多级检测器的应用[J].无线电通信技术,2000,26(3):36-37,56.
[13] 白林,张一琼.OFDM系统中基于软干扰抵消的Turbo均衡算法研究[J].无线电通信技术,2015,41(4):61-63,83.
