基于LPP的转子振动故障特征提取方法

梁 超， 路 鹏， 郜 宁， 祁 伟

(国网新疆电力有限公司电力科学研究院， 新疆 乌鲁木齐 830000)

引 言

转子作为旋转机械的重要组成部件，其能否正常运转直接关系到旋转机械的工作状态。而转子在故障发生初期，由故障引起振动信号被淹没在背景噪声中，传统的时频分析方法以偏度、峭度等作为诊断指标，在提取故障特征之前需要对信号预处理去噪，往往受制于信号的非线性和非平稳性以及是否被噪声污染[1-2]。针对故障的非线性和非平稳性，霍天龙等[3]提取故障信号的奇异值谱熵、功率谱熵、小波空间谱熵和小波能谱熵作为特征量，并结合SVM分类器实现了转子故障诊断，取得了较好的效果。张超等[4]针对转子复合故障诊断问题，提出了基于第2代小波和极值域均值模式分解的故障特征提取方法。文献[5-6]将经验模式分解和Hilbert-Huang变换引入到转子故障特征提取中，取得了很好的诊断效果。由于转子系统结构及工作状态的复杂性，载荷、间隙、摩擦力、刚度等非线性因素的影响程度不同，有时很难仅通过时域或频谱分析来对转子系统的工作状态做出较为准确的评价。小波分解频带中包含的大量信号往往造成特征的敏感性降低，增加了分类和智能识别的困难[7-8]，经验模式分解方法仍存在端点延拓和模态混叠等问题。

目前，主成分分析(Principle Component Analysis, PCA)、线性判别分析(Linear Discriminant Analysis)和独立分量分析(Independent Component Analysis, ICA)等线性方法已用于故障特征提取中。这些算法在数据的全局线性结构假设下，采用不同的优化准则来寻求最佳线性模型，将高维观测数据映射到一个低维线性子空间中。但是，由于振动信号的非线性、非平稳特性，导致振动信号存在着局部的非线性结构，这些非线性结构往往对分类起着重要作用，在这种情况下，采用新的降维方法就显得十分必要。

LPP算法最早由何晓飞[9]于2003年提出，其主要思想为通过给出输出的线性映射关系取代Laplacian Eigenmap中的非线性映射关系，从而实现从高维观测空间到低维特征空间的线性映射。与PCA不同的是，PCA是基于统计模型的，很难发现数据流形的几何特征，LPP在线性条件下可以尽量保持原始流形的局部几何特征[10-12]。为了从故障信号中提取出有效的敏感特征，本文提出了一种基于局部保持投影(Locality Preserving Projections, LPP)的转子诊断故障特征提取方法。实验证明LPP算法提取出的特征可以有效地完成不同类别信号的分类。

1 LPP算法

LPP具体算法如下：

设样本数据X={x1，x2，…，xn}，xi∈RD(i=1，2, …,n)。A为投影矩阵,LPP算法通过变换yi=Axi将RD空间中的点集X映射到Rd空间中得到Y={y1，y2，…，yn}，yi∈Rd(i=1，2, …,n)。

(1)建立邻域连接图。使用k近邻的方法构造邻域连接图，如果xi是样本xj的k个欧式距离最近的样本之一，那么在邻域图上样本xi与xj连接。

(2)确定权值。如果xi是xj的k近邻或者xj是xi的k近邻，那么两个样本之间的权值为Wij= exp(-‖xi-xj‖2/t)，式中t是一个常数。

(3)计算特征值。求解下式的最小特征值以及对应的特征向量

XLXTa=λXUXTa

式中U是对角阵，Uij=∑jWji；L=U-W，是Laplacian矩阵。

(4)设Y={a0，a1，…，ak-1}为上式的解，对应的特征值为λ0<λ1<…<λk-1，则嵌入映射为：

xi→yi=YTxi

yi就是所求的d维向量，Y是一个d×k的矩阵。

局部保留投影(LPP)本身是通过求解一个不对称特征方程的最小特征值所对应的特征向量进行投影，因此能够保留信号的局部邻域结构。核方法是通过一个非线性映射将低维数据映射到高维空间中，但其泛化能力依赖于样本的几何特性，与选取的样本关系较大。

2 基于LPP的故障特征提取方法

为了提取出隐藏在振动信号中的故障特征，本文利用一维时间序列(振动信号)构造了一个D×N的高维特征矩阵[13-14]。在故障样本数据较少的情况下，该矩阵也能体现故障的特征。

2.1 高维特征矩阵构造

设一维时间序列S(c1，c2，…，ct，…)是采集到的振动信号，如图1所示。

图1 振动信号图Fig.1 Vibration signal figure

首先找到振动通过平衡位置向正位移方向运动时的点，如图中所示的A1,B1,C1和D1点。然后分别以A1,B1,C1,…等点作为一个样本的起点，截取长度为D的时间序列xi(c1，c2，…，cD)作为一个样本，将所有样本组成一个集合X={x1，x2，…，xN}，称作高维特征矩阵。该方法相对于相空间重构，对故障分类效果更加明显。具体构造步骤如下：

(1)找出S中所有的峰值点，标记峰值点的位置。

(2)对所有峰值点取绝对值，然后求其平均值，如果峰值点大于平均值，则保留峰值点，否则去除它。得到的保留峰值为X(X1,X2,…,XN)。

(3)以第2步的保留峰值作为起始点截取长度为∂的m维相空间，每一个m维向量都是重构相空间中的点X(X1,X2,…,XN)，即是所要构造的m×N高维矩阵。

中间(m-1)τ=∂，嵌入维数用m表示，延迟时间用τ代表，这2个参数对于相空间的结构影响非常大。通过上面的方式得到了高维特征矩阵X={X1,X2,…,XN}。

2.2 故障特征提取

对于高维特征矩阵X={x1，x2，…，xN}，利用LPP算法把数据从高维空间投影到低维空间，得到一个低维数据集合Y={y1，y2，…，yN}，这个矩阵就是低维特征矩阵，低维矩阵保留了高维矩阵的特征，其中xi与yi(i=1，2，…，N)是一一对应的关系。如图2所示，从不同类型的信号中分别提出D×N高维特征矩阵，然后将所有的高维特征矩阵同时利用LPP算法统一降维，得到d×N的低维矩阵，即为低维特征矩阵。

图2 特征提取流程图Fig.2 Flowchart of feature extraction

以上方法得到低维特征矩阵保留了原有数据的属性，可将低维特征矩阵中的特征向量投影到对应的空间中，同类信号的特征向量将会投影到相同或相近的区域中，实现与其他类别信号的分离。

3 诊断应用实例分析

3.1 数据采集

转子振动实验台(如图3所示)模拟振动信号，人为制造一些故障来模拟汽轮机转子的振动。实验装置包括：ZT-3型转子振动实验台、ZXP-4A型数字测振仪主机、信号采集器、电涡流传感器、计算机以及DASP等。

图3 转子振动实验台Fig.3 Experiment of rotor vibration

模拟的故障分为3类，包括：转子质量不平衡、不对中以及松动和不对中耦合。各种故障模拟的方法为：不平衡故障通过在临近电涡流传感器的转子转盘上旋入3～5个螺钉，螺钉要集中以使转子发生不平衡故障；不对中故障是将联轴器换成硬质橡胶管，并在轴末端的轴承座底垫上1～2个垫片，人为地将轴承座扭转一定角度实现；松动和不对中故障耦合则是在一次实验中加入轴承座松动和转子不对中两种故障实现。

实验台在直流电动机的驱动下工作。联轴节可使转子发生旋转。实验中的支撑点沿轴向任何部位随机选取。试验台轴均采用滑动轴承支撑，转子采用锥套式锁紧方式固定在轴上，使用电涡流传感器测量轴对轴承座的相对位移和振动，测得的振动数据经过转换输入到计算机中。

故障信号的原始采样频率为1000 Hz，采样点数为8000点，实验中，转子转速分为1000 r/min，1150 r/min和1200 r/min三种。每个转速下每种故障各采样10组数据。

图4 原始信号波形图Fig.4 Original vibration signals

图4为3类故障信号的波形图，不对中信号相对于其他两种信号比较平滑，出现的局部尖峰点比较少，这是由于联轴器对中不良造成的；不平衡信号振动比较强烈，局部尖峰点比较多，这是由于质量不平衡而发生较为强烈的振动引起的。从整体上看，3类信号都表现出了一定的周期性特征，在长度为100个采样点的范围内每个信号大约有3.5个近似周期；观察振动信号的局部波形特征，发现有一些特有的波形会重复出现，而且各类振动信号的局部特有波形不同。

3.2 测试分类效果

根据2.1节的高维特征矩阵构造方法，故障分别构造一个200×100高维特征矩阵。用LPP算法对3类故障的高维特征矩阵组成的集合进行统一数据降维。图5是选取每个特征向量的第一分量与第二分量、第一分量与第三分量的二维投影图。从图5(a)可以看出，不对中和不对中+松动有很大的重叠，而不平衡与这两种故障区分较好。从图5(b)可以看出，第一分量和第三分量能够初步将3类故障分开，但不对中和不对中+松动仍有小部分重叠，因而需要进一步采用分类器来诊断。

对3类

图5 特征向量的二维分类效果图Fig.5 Two dimensional classification of feature vectors

3.3 故障诊断方法

为了验证LPP的有效性，本文采用BP神经网络的方法建立故障诊断模型。BP神经网络具有很强的非线性映射能力、自学习适应能力和容错能力，将其应用于故障诊断预测时，具有预测精度较高、训练速度快等优点。

图6给出了基于LPP和BP人工神经网络的故障诊断流程。流程分为两大部分，一是用已知信号的特征向量训练BP网络；二是将待测未知信号的特征向量输入BP网络中进行分类识别。选取第一组故障信号作为已知信号，包括不对中，不对中加松动和不平衡3类故障，从其余几组数据中分别取不对中，不对中加松动和不平衡信号作为未知信号。将3类故障信号和未知信号的高维特征矩阵组成的集合用LPP算法降维，用已知的3类故障信号对应的特征向量作为BP网络的训练样本，未知信号对应的特征向量作为测试样本。

图6 故障诊断流程图Fig.6 Process of fault diagnosis

BP神经网络采用运算速度最快、最稳健的Levenberg-Marquardt算法，确定隐层节点数为11，输出节点数为3，训练精度为0.0001。每类故障信号取100个特征向量作为训练样本，未知信号取120个特征向量作为测试样本。诊断在Pentium(R) D, CPU2.66 GHz, 1.0 G内存的计算机上进行。当特征维数为2～9时的故障诊断结果如表1所示。

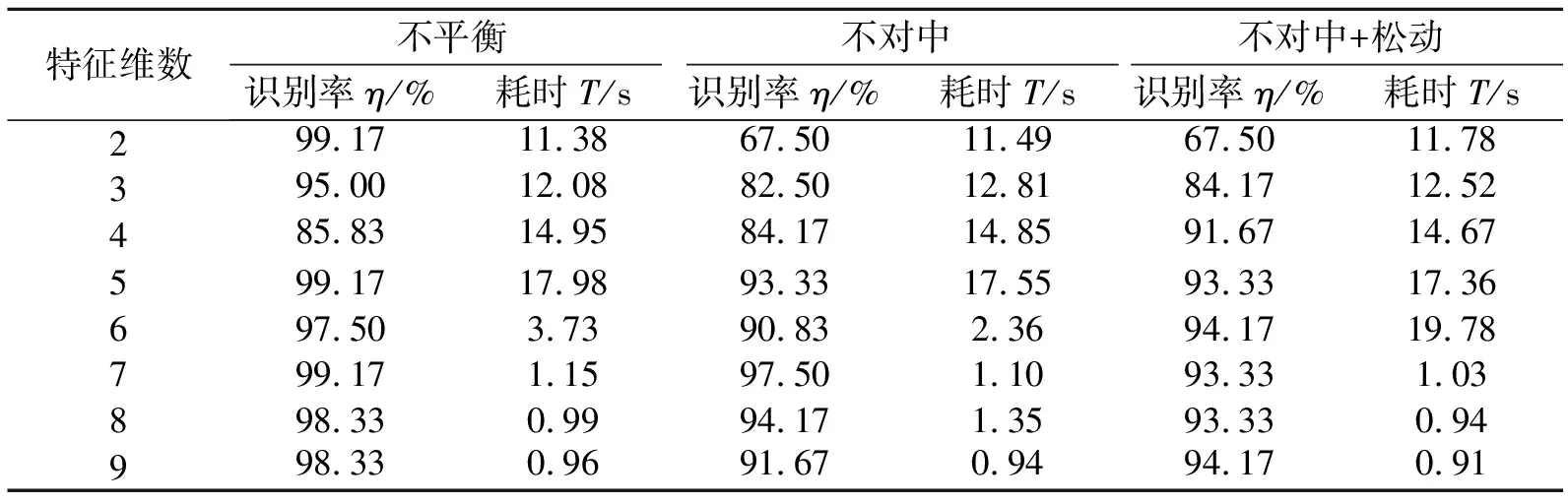
表1 故障诊断结果

3.4 参数分析

3.4.1 样本长度

样本长度N是构造高维特征矩阵的一个重要参数，对故障诊断识别率有很大影响。图7和8的给出了样本长度(50～500)与不同故障的总体识别率曲线。每类故障选取150个样本(其中前100个训练样本，其余50个样本为测试样本)构造高维特征矩阵，N=200，LPP提取的特征向量维数m=9。从图中可以看出识别率曲线表现出了波动变化，说明N的大小对故障诊断识别率有一定的影响，但是从整体上看，识别率保持在一个较高的水平。考虑计算量的大小，一般取较小的N值。

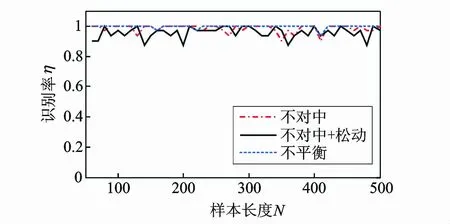
图7 样本长度对不同故障识别率的影响Fig.7 Effect of sample length on different fault recognition rate

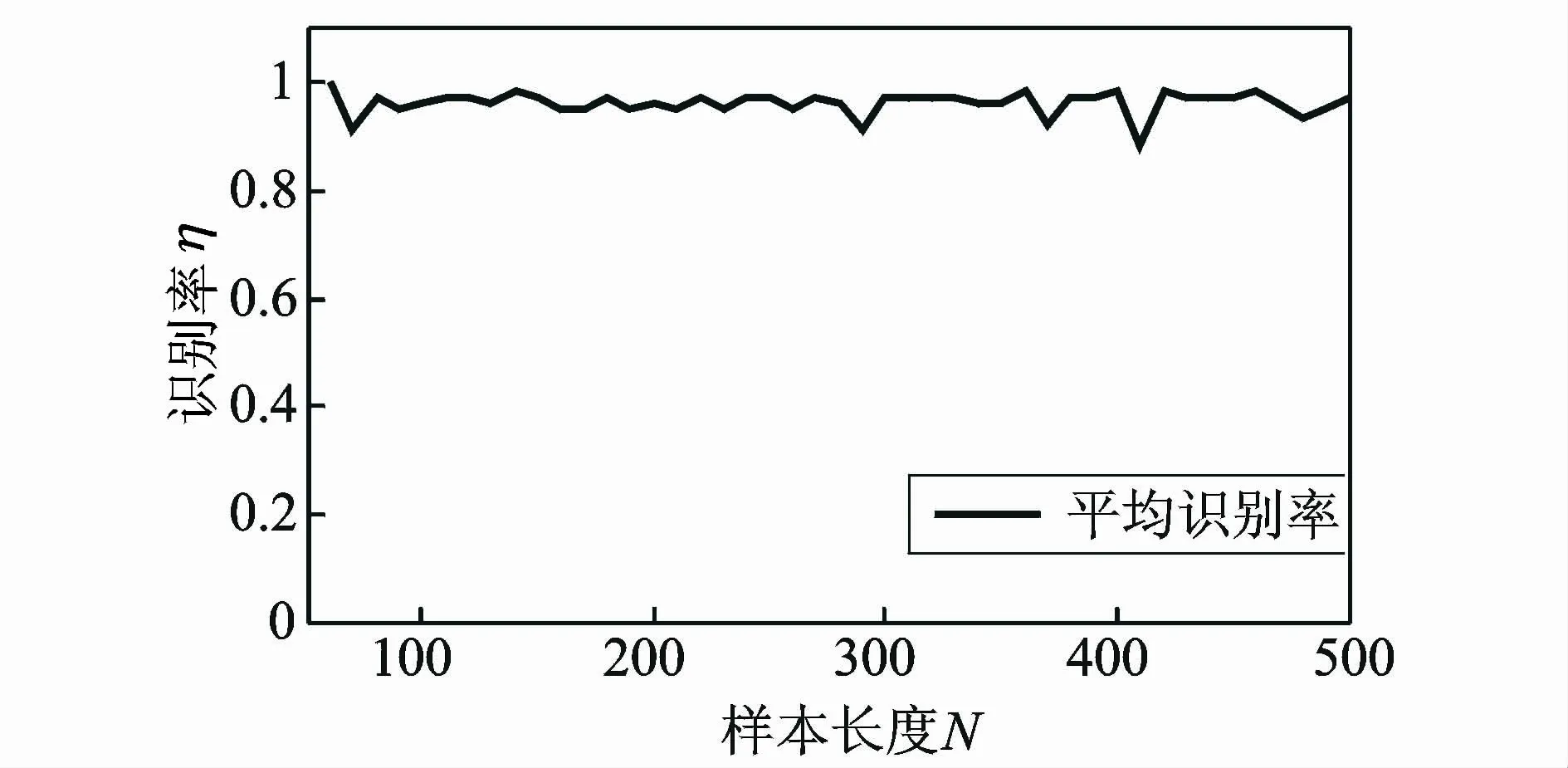
图8 样本长度对总体识别率的影响Fig.8 Effect of sample length on the overall recognition rate

3.4.2 特征向量的维数

从表1可知特征向量的维数m对故障诊断识别率和诊断速度有较大的影响。图9给出了识别率随特征维数m的变化曲线。可以看出，当特征维数m>7时识别率有了明显的提高，从整体上看，随m的增大识别率出现较大的波动。但是m过大会影响BP网络训练的收敛速度，取值不宜过大。当m取2～4时，识别率较低并且诊断耗时较长，需要10 s左右；当m取7～14时，识别率达到85%以上，诊断用时1 s左右。这是因为m较大时，LPP算法提取特征向量的可分性较好。随着m的进一步增大，特征向量的可分性出现较大波动，从而导致识别率波动较大。

图9 特征维数对故障识别率的影响Fig.9 Effect of feature dimension on fault recognition rate

为进一步体现本文方法的优越性，与小波能量、小波包能量两种特征提取方法进行了比较，分类器均采用BP网络，结果如表2所示。小波能量特征采用Db2小波分解4层，提取6个频带能量特征，相应BP网络的输入节点数为6，隐层节点数取8，输出节点数为3。小波包能量特征采用Db2小波包分解3层，提取8个频带能量特征，相应BP网络的输入节点数为8，隐层节点数取10，输出节点数为3。根据3.4节的分析结果，LPP方法采用的样本长度N=200，特征维数m=11。从表2中可以看出，本文方法具有更好的诊断效果，诊断率达96.67%。

表2 不同特征提取方法的比较

4 结 论

本文提出了一种基于LPP算法的转子振动故障特征提取方法，并探讨了该算法在实际应用中的可行性。用LPP算法对振动信号进行特征提取，并采用BP神经网络分类器完成故障诊断。结果表明该方法的可行和有效，与小波能量和小波包能量特征相比，具有更高的诊断率。文中分析了样本长度N和特征维数m对故障诊断识别率的影响，为了减少计算量和缩短计算时间，在构造高维特征矩阵时N不宜选取过大，m也尽量选择较小的值。

[1] 马 辉，赵 鑫，赵群超，等. 时频分析在旋转机械故障诊断中的应用[J]. 振动与冲击，2007，26(3)：61—65.

Ma Hui, Zhao Xin, Zhao Qun-chao, et al. Application of time-frequency analysis to rotating machinery fault diagnosis[J]. Journal of Vibration and Shock, 2007,26(3):61—65.

[2] 胡爱军，安连锁，唐贵基. 转子碰摩故障振动时频特征的实验研究[J]. 动力工程，2007，27(4)：483—488.

Hu Ai-jun, An Lian-suo, Tang Gui-ji. Experimental study on time-frequency characteristics of rubbing initiated vibration of rotor[J]. Journal of Power Engineering, 2007,27(4):483—488.

[3] 霍天龙，赵荣珍，胡宝权. 基于熵带法与PSO优化的SVM转子故障诊断[J]. 振动、测试和诊断，2011，31(5)：552—556.

Huo Tian-long, Zhao Rong-zhen, Hu Bao-quan. Fault diagnosis for rotor systems based on entropy band method and support vector machine optimized by PSO[J]. Journal of Vibration, Measurement & Diagnosis, 2011,31(5):552—556.

[4] 张 超，陈建军，郭 讯. 基于第2代小波和EMMD的转子系统复合故障诊断[J]. 振动、测试和诊断，2011，31(1)：98—103.

Zhang Chao, Chen Jian-jun, Guo Xun. Complex fault diagnosis for rotor systems using the second generation wavelet and extremum field mean mode decomposition[J]. Journal of Vibration, Measurement & Diagnosis, 2011,31(1):98—103.

[5] 于德介，陈淼峰，程军圣，等. 一种基于经验模式分解与支持向量机的转子故障诊断方法[J]. 中国电机工程学报，2006，26(16)：162—167.

Yu Dejie, Chen Miaofeng, Cheng Junsheng, et al. A fault diagnosis approach for rotor systems based on empirical mode decomposition method and support vector machines[J]. Proceeding of the CSEE, 2006,26(16):162—167.

[6] 向 玲，朱永利，唐贵基. HHT方法在转子振动故障诊断中的应用[J]. 中国电机工程学报，2007，27(35)：84—89.

Xiang Ling, Zhu Yong-li, Tang Gui-ji. Application of Hilbert-Huang transform method in vibration faults diagnosis for rotor system[J]. Proceedings of the CSEE, 2007,27(35):84—89.

[7] 许 琦，吴 昊，赵立超，等. 多跨转子系统耦合故障定量诊断方法[J]. 振动工程学报，2015，28(3)：495—500.

Xu Qi, Wu Hao, Zhao Li-chao, et al. Quantitative coupling fault diagnosis method of multi-span rotor based on harmonic components[J]. Journal of Vibration Engineering, 2015，28(3)：495—500.

[8] 张 弦，王宏力. 基于WT与LSSVC的信号消噪方法及其在转子故障诊断中的应用[J]. 振动工程学报，2010，23(3)：348—353.

Zhang Xian, Whang Hong-li. Wavelet denoising using least squares support vector classifier and its application to rotor fault diagnosis[J]. Journal of Vibration Engineering, 2010,23(3):348—353.

[9] Xiaofei He, Partha Niyogi. Locality preserving projections[J]. Advances in Neural Information Processing Systems, 2003:16(1):186—197.

[10] 屈晓刚，何明一，梅少辉. 一种改进的局部保持投影高光谱特征提取算法[J]. 现代电子技术，2011，34(13)：74—80.

Qu Xiao-gang, He Ming-yi, Mei Shao-hui. An improved algorithm for hyperspectral data feature extraction in locality preserving projections[J]. Modern Electronics Technique, 2011,34(13):74—80.

[11] 金 一，阮秋琦. 基于核的正交局部保持投影的人脸识别[J]. 电子与信息学报，2009，31(2)：283—287.

Jin Yi, Ruan Qiu-qi. Kernel based orthogonal locality preserving projections for face recognition[J]. Journal of Electronics & Information Technology, 2009,31(2):283—287.

[12] 尹海兵，刘 兆，刘亚东，等. 基于局部保持投影的神经尖峰电位特征提取与分类[J]. 计算机应用，2010，30(9)：2559—2563.

Yin Hai-bing, Liu Zhao, Liu Ya-dong, et al. Unsupervised spike extraction and classification based on locality preserving projection[J]. Journal of Computer Applications, 2010,30(9):2559—2563.

[13] 黎 敏，徐金梧，阳建宏，等. 一种基于流形拓扑结构的轴承故障分类方法[J]. 控制工程，2009，16(3)：358—362.

LI Min，XU Jinwu，YANG Jianhong，et al. Classification method of bearing faults based on topological structure of manifold[J]. Control Engineering of China，2009，16(3)：358—362.

[14] 阳建宏，徐金梧，杨德斌，等.基于相重构和主流形识别的非线性时间序列降噪方法[J]. 北京科技大学学报，2005，27(5)：631—634.

Yang Jian-hong, Xu Jin-wu,Yang De-bin, et al. Nonlinear time series noise reduction method based on phase reconstruction and principal manifold learning[J]. Journal of University of Science and Technology Beijing, 2005,27(5):631—634.