基于频域和时域振动模型的轨道交通桥梁噪声预测对比分析
2018-07-05宋晓东
宋晓东, 石 宇, 李 奇
(1.东南大学桥梁与隧道工程系, 江苏 南京 210096; 2.同济大学桥梁与隧道工程系, 上海 200092)
引 言
当列车通过轨道交通高架桥梁时,会引起桥梁结构的振动,进而引起桥梁的辐射噪声,这使得高架系统的噪声水平一般要高于同等情况下的普通线路噪声水平[1]。在中国,轨道交通系统正处于快速发展时期,且高架桥梁在线路中所占的比例很高,其引起的噪声问题引起了越来越多的关注。为了研究桥梁的辐射噪声问题,国内外学者提出了多种计算方法来预测桥梁的结构噪声[2-10]。
在进行桥梁振动辐射噪声预测时,桥梁振动响应是进行声学计算的基础。由于车致桥梁结构振动为一个时变过程,因此一些学者采用时域的车辆-轨道-桥梁耦合振动模型来获得桥梁的动态响应[3-7]。李小珍等[3]结合时域车桥耦合分析和频域声学边界元(BEM)方法对高速铁路的箱梁噪声问题进行了研究。张迅等[4]通过时域车桥耦合分析获得轮轨力,然后将轮轨力转化到频域,结合混合有限元(FEM)-统计能量法(SEA)对箱梁各板件的噪声贡献量进行了分析。张鹤等通[5]结合时域的车桥耦合振动模型和瞬态边界元方法对某公路钢桥的噪声特性进行了研究。作者采用基于空间波数变换的2.5维方法计算了某U型梁的声模态传递向量,并结合时域的车桥耦合预测了桥梁的噪声[6-7]。
由于时域的车桥耦合计算模型需要对整个车辆-轨道-桥梁系统求解动力微分方程,且在采用频域声学计算时还要将时域的桥梁振动响应转化到频域,使得计算量较大。一些学者提出了频域的车辆-轨道-桥梁耦合振动模型[1,8-10],在获得车轮、轮轨接触弹簧和钢轨的振动导纳后,可以通过解析解直接获得轮轨力,其计算量较时域方法要小很多。李增光等[8]通过频域的车辆-轨道-桥梁耦合模型分析了轮轨不平顺激励下传递到轨道交通箱梁结构的振动功率。吴天行等结合频域耦合振动模型和声学边界元方法对比了箱梁和U型梁的辐射声功率[9]。Bewes等[1]采用频域振动模型和统计能量法计算了某铁路钢桥的振动响应,然后结合声辐射效率对其辐射噪声进行了预测分析。李奇等[10]提出了基于力法的功率流频域振动耦合模型,并结合二维有限元/无限元声学模型对桥梁、钢轨的辐射噪声进行了研究。频域振动模型比时域振动模型更容易求解,但也存在一些缺点:频域模型只能采用线性的轮轨接触关系,而时域模型可以考虑非线性接触;频域模型一般多采用移动粗糙度激励模型,无法精确模拟车轮过桥时的动态过程;频域模型一般采用单轮对车辆模型,不能准确考虑相邻车轮的相互影响。
虽然众多学者采用时域或频域车桥耦合振动模型对桥梁的振动声辐射进行了大量的研究,但是这两种方法的基本假定和求解思路并不相同,获得的桥梁振动响应存在一定的差异,两种模型的计算结果差别以及预测精度仍然有待研究。很少有文献专门对比这两种方法在计算桥梁振动和辐射噪声时的差别。本文以某U型梁桥为背景,同时采用时域和频域车辆-轨道-桥梁耦合振动模型对桥梁的振动响应进行分析,进而通过声学边界元来预测桥梁的声辐射。通过对比两种方法获得的轮轨力、桥梁振动加速度、场点声压等指标,全面对比两种振动模型在用于桥梁噪声预测时的异同。
1 桥梁振动声辐射计算
1.1 频域振动模型
由于车辆一系悬挂和二系悬挂的频率一般低于20 Hz,因此在研究结构噪声时可以忽略车辆悬挂的影响,采用简化的车轮模型。对于轨道交通桥梁,一般车速远低于钢轨振动波速,因此可以采用移动粗糙度的激励模型,频域的车辆-轨道-桥梁耦合振动模型如图1所示。车轮通过线性Hertz弹簧与钢轨连接,其中只有主动轮受到粗糙度的激励,而被动轮仅考虑其质量效应[11],不受到粗糙度的激励。本文只考虑轮轨竖向作用,不考虑横向效应。钢轨与桥梁、地面之间用弹簧、阻尼单元连接。
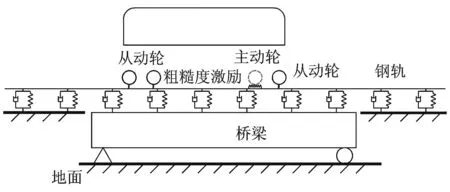
图1 车辆-轨道-桥梁耦合模型Fig.1 Vehicle-track-bridge interaction model
在移动粗糙度激励作用下,轮轨动态作用力可以表示为[12]
(1)

在求得轮轨动态力后,可以进一步对整个系统进行频域的振动分析以获得桥梁的动力响应,然后结合频域的声学边界元模型计算桥梁的辐射声压。
1.2 时域振动模型
本文采用李奇[14]提出的基于模态叠加法的时域车辆-轨道-桥梁耦合振动分析方法,其中车辆采用多刚体整车模型(包含车体、转向架和悬挂系统)以考虑多轮对之间的相互影响,钢轨和桥梁采用有限元模型计算获得其各阶模态,车辆、钢轨和桥梁各子系统之间的弹簧和阻尼连接用虚拟激励荷载表示,整个系统的动力方程如下
(2)
式中q,ξ,Φ和ω分别代表模态坐标矩阵、模态阻尼矩阵、模态位移矩阵和模态圆频率矩阵;f为荷载矩阵,包括动态轮轨作用力、各系统间连接的非线性阻尼和弹簧对应的虚拟激励荷载[14];下标v,t和b分别为车辆、轨道和桥梁子系统;上标T代表矩阵转置。
由方程式(2)可以获得时域的桥梁模态坐标时程qt,通过快速傅里叶变换(FFT)则可以得到桥梁模态坐标频谱Qb(ω)。然后利用频域声学边界元方法计算桥梁的各阶声模态传递向量 (Modal Acoustic Transfer Vectors,简称MATV)。桥梁声压谱P(ω)可以表示为[7]
P(ω)=MATV(ω)TQb(ω)
(3)
2 频域和时域模型对比
2.1 工程背景
本文以某轨道交通简支U型梁桥为工程案例,分别采用频域方法和时域方法对该桥的振动和声辐射进行预测,并进行对比分析。该桥梁主跨为25 m,腹板、顶底板厚度均为240 mm,如图2所示。

图2 U型梁截面图 (单位:mm)Fig.2 Cross section of the U-shaped girder (Unit: mm)
2.2 模型及参数
桥梁有限元模型采用Ansys商业软件中的Solid45实体单元建立(包括轨下承轨台部分),钢轨采用Beam188空间梁单元建立,二期恒载用质量单元模拟。为了保证仿真分析时车辆进入桥跨时的平顺性,并降低边界反射对钢轨振动的影响,在单跨桥梁模型两侧各建一跨钢轨,并与地面连接,有限元模型如图3所示。钢轨和桥梁/地面之间用扣件连接(间距0.6 m),在频域振动模型中扣件采用弹簧阻尼单元模拟,扣件参数如表1所示;在时域振动模型中,扣件的弹簧和阻尼力处理为虚拟激励荷载,不在有限元模型中直接模拟[14]。

图3 桥梁有限元模型Fig.3 Finite element model of the bridge

参数数值扣件纵向刚度20 MN/m扣件竖向刚度60 MN/m扣件横向刚度20 MN/m扣件纵向阻尼60 kN·s/m扣件竖向阻尼80 kN·s/m扣件横向阻尼60 kN·s/m单个车轮质量908 kg转向架间距12.6 m轮对轴距2 m轮轨接触弹簧刚度1300 MN/m
时域模振动模型采用采用7节动车编组整车模型,车速为70 km/h,只考虑竖向轮轨力,不计横向力,具体的车辆参数见文献[15]。频域振动模型中车辆采用车轮模型模拟,车轮参数如表1所示。25 m跨径的桥梁主跨范围内最多能同时布置一辆车,因此2根钢轨上共有8个车轮,其中1个作为主动轮;另外7个作为从动轮,用质量单元模拟,仅考虑车轮与钢轨间的竖向作用并通过弹簧单元与钢轨连接,在横向与纵向则与钢轨直接耦合。为了考虑不同轮对位置对结构振动的影响,本文将8个轮对逐个作为主动轮(剩下的7个作为从动轮),将一侧钢轨的4个车轮从左到右作为主动轮分别称为工况1-4,另一侧钢轨相应的车轮分别称为工况5-8。时域和频域模型的钢轨粗糙度谱均采用ISO3095规范[16]中的不平顺限值谱,波长范围为0.04~100 m,其中时域的不平顺样本采用三角级数法生成[14]。
通过两种振动模型获得桥梁的动态响应后,建立相应的边界元声学模型进行声学计算,最大单元尺寸为0.2 m,以满足1个波长至少划分6个单元的要求,结构外表面考虑为全刚性。边界元模型由有限元模型提取表面网格获得,以便于结构振动边界条件的映射。时域振动模型通过2.5维方法获得声模态传递向量[6],然后结合式(3)预测桥梁辐射噪声。频域振动模型则直接采用三维声学模型进行计算,计算频率间隔取2 Hz,可满足1/3倍频程的计算精度要求。
2.3 频域模型验证
通过频域有限元模型可以计算获得钢轨驱动点(driving point)的导纳,并用文献[10]中基于力法的功率流模型计算结果进行对比,如图4所示。文献[10]中的钢轨采用铁摩辛柯梁理论模型,桥梁采用有限元模型。由图4可知,本文的有限元模型计算结果与文献[10]获得的结果吻合较好。

图4 钢轨驱动点导纳Fig.4 Driving point mobility of the rail
然后,利用公式(1)计算获得动态轮轨力,如图5所示,两种方法计算获得的结果基本一致,进一步验证了有限元模型的准确性。由图5可知,轮轨力的峰值频率为54 Hz左右,对应着车轮-轨道系统的自振频率[13]。

图5 轮轨力频谱Fig.5 Spectrum of the wheel-rail contact force
2.4 振动响应
首先,通过时域振动模型获得轮轨力的时程,经过傅里叶变换后得到其频谱,并与频域振动模型的轮轨力频谱进行对比,如图6所示。由图6可知,对于频域模型,不同主动轮位置对轮轨力的影响不大,各工况计算获得轮轨力基本一致,多轮对的影响较小。频域振动模型获得的轮轨力频谱曲线与时域振动模型的结果趋势一致,峰值点频率都位于64 Hz,但是在各1/3倍频程点上的幅值略有区别。频域振动模型可以用于计算列车过桥时的轮轨接触力。

图6 两种模型轮轨力频谱图Fig.6 Spectrum of the wheel-rail contact force for two models
然后,采用两种振动模型计算桥梁的动力响应,分别选取跨中和1/4跨承轨台(轨下位置)位置。时域模型的加速度时程选取列车通过时间段的样本并转化到频谱。在采用频域振动模型计算桥梁某一位置的加速度时,由于主动轮的激励位置不同,其传递导纳也不一样,因此需要考虑不同主动轮的影响。一般而言,在分析20 Hz以上的1/3倍频程振动和声辐射时,可以认为各车轮的激励是非相干源,从而采用叠加原理来考虑多个车轮的激励效应[13]以获得总的振动响应。在此,将两侧钢轨8个车轮分别作为主动轮逐一进行计算,最后将8个主动轮的计算结果进行叠加得到桥梁的加速度。频域模型和时域模型计算获得的桥梁加速度级如图7所示。由图7可知,总体来说,频域振动模型的计算结果与时域模型的结果趋势一致,吻合较好。采用频域振动模型可以较为准确地模拟桥梁的振动加速度。

图7 两种模型桥梁加速度级Fig.7 Acceleration levels of the bridge for two models
2.5 辐射声压
基于两种模型的振动计算结果,可以进一步获得相应的辐射声压。由于频域振动模型每次只能考虑一个车轮的激励,结构的振动响应为8个车轮的激励效应的叠加,因此严格来说,应当分别建立相应的振动声辐射模型,计算8个主动轮工况下的辐射声压,最终按照不相干声源进行叠加获得总声压。但是,三维声学边界元计算较为费时,同时由图8可知,不同主动轮工况下传入桥梁的振动功率相差不大,忽略多轮对的影响。因此可以近似认为8个工况计算得到的声压结果相同,再按照非相干源叠加获得总的声压。

图8 传入桥梁的功率Fig.8 Power transmitted into the bridge
为了对比两种模型计算的辐射声压,设置了3个场点,竖向均位于U型梁底板中心线以下4.8 m高处,而横向距离不同,如图9~11所示。由图可知,除了在个别频率点外,基于频域振动模型和时域振动模型预测获得的不同场点的声压频谱曲线整体趋势和幅值都吻合较好。
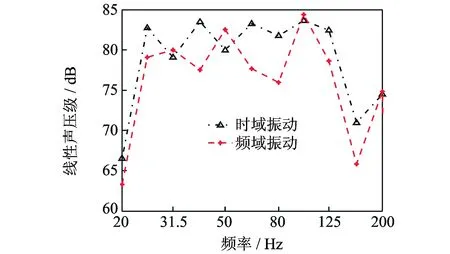
图9 梁底中心线以下4.8 m高处场点声压Fig.9 Sound pressure at the field point 4.8 m beneath the bridge bottom slab

图10 梁底中心线以下4.8 m高、7.5 m远处场点声压Fig.10 Sound pressure at the field point 4.8 m beneath the bridge bottom slab and 7.5 m away from the center
为了进一步对比两种振动模型噪声预测结果的差异性,图12(a)和(b)分别给出了基于时域振动和频域振动模型预测得到的桥梁噪声等高线图,其中原点设置在U型梁底板中心位置。由图12可知,除了距离梁底1~4 m、轨道中心线5~10 m范围,两种模型在其余空间位置的噪声分布形状和数值都吻合较好。图12(c)为两种模型预测结果差值的等高线图,在绝大部分空间区域内,两者的差值小于2 dB,在离轨道中心线30 m全空间范围内两者的差值小于3 dB。由此可见,在计算频域振动模型的辐射声压时,本文采用近似的声源处理方法可以获得较好的计算精度。

图11 梁底中心线以下4.8 m高、30 m远处场点声压Fig.11 Sound pressure at the field point 4.8 m beneath the bridge bottom slab and 30 m away from the center
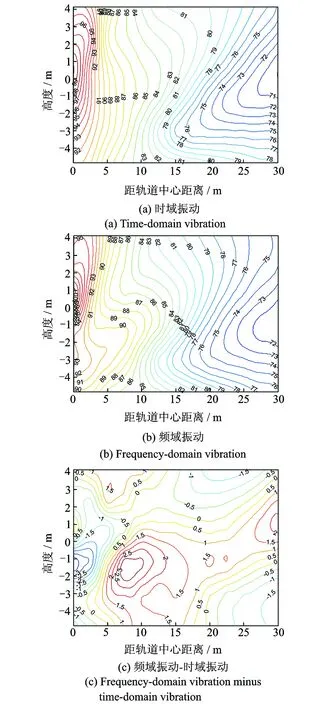
图12 桥梁噪声等高线图Fig.12 Contour maps of the bridge noise
从图12的噪声分布情况可知,桥梁辐射噪声有较强的指向性,而传统的简化偶极子线声源模型无法准确模拟其指向性。因此,需要采用精细的振动声辐射模型。图13给出了基于频域振动模型计算获得的桥梁声辐射效率。由图可知,U型梁的声辐射效率在低频较小,随着频率的提高,该值逐渐增加,到100 Hz以上,声辐射效率基本接近于1,说明U型梁在高频的声辐射能力大于低频的辐射能力。

图13 桥梁声辐射效率Fig.13 Noise radiation ratio of the bridge
3 结 论
本文采用时域和频域的车辆-轨道-桥梁耦合振动模型计算了某U型梁的车致振动响应,然后基于两种振动模型对桥梁的辐射噪声进行了预测,并对两种模型的计算结果进行了全面对比分析。本文结论如下:
(1) 频域振动模型和时域振动模型获得的轮轨力频谱基本一致,都能准确反映车轮-轨道系统的自振频率。
(2)两种振动模型计算得到的桥梁振动加速度频谱吻合较好,频域振动模型需要考虑不同车轮作为主动轮的多工况影响。
(3)两种振动模型获得的桥梁辐射噪声频谱和总声压等高线分布图都吻合较好,可以用频域振动模型来快速预测桥梁的辐射噪声。
[1] Bewes O G, Thompson D J, Jones C J C, et al. Calculation of noise from railway bridges and viaducts: experimental validation of a rapid calculation model[J].Journal of Sound and Vibration,2006,293:933—943.
[2] 王小宁,张 楠,孙 奇.城市轨道交通桥梁振动及噪声辐射研究[J]. 铁道建筑,2014(1):11—15.
Wang Xiaoning, Zhang Nan, Sun Qi. Study on vibration and noise radiation of urban rail transit bridges[J].Railway Engineering, 2014(1):11—15.
[3] 李小珍,张 迅,李亚东.高速铁路简支箱梁结构噪声的边界元方法[J].土木工程学报,2011,44(S1):95—101.
Li Xiaozhen,Zhang Xun,Li Yadong. Application of boundary element method in study of noise from simply-supported box girder in high speed railway[J].China Civil Engineering Journal,2011,44(S1):95—101.
[4] 张 迅,张健强,李小珍. 混合FE-SEA模型预测箱梁低频噪声及试验验证[J]. 振动工程学报,2016,29(02):237—245.
Zhang Xun, Zhang Jianqiang, Li Xiaozhen. Hybrid FE-SEA model and test validation for box-girders radiated low-frequency noise[J]. Journal of Vibration Engineering,2016,29(02):237—245.
[5] 张 鹤,谢 旭,山下幹夫.交通荷载引起的钢箱梁桥振动辐射瞬态噪声评估[J].振动工程学报,2011,24(3):221—228.
Zhang He,Xie Xu,Yamashita Mikio. Assessment of sound pressure of transient noise radiated from vehicle-bridge coupling vibration [J]. Journal of Vibration Engineering,2011,24(3):221—228.
[6] 宋晓东,吴定俊, 李 奇.基于无限元的2.5维方法预测轨道交通混凝土桥梁低频噪声[J]. 振动工程学报, 2015,28(6):929—936.
Song Xiaodong, Wu Dingjun, Li Qi. A 2.5-dimensional infinite element based method for the prediction of structure-borne low-frequency noise from concrete rail transit bridges[J].Journal of Vibration Engineering, 2015, 28(6):929—936.
[7] Song X D, Wu D J, Li Q, et al. Structure-borne low-frequency noise from multi-span bridges: a prediction method and spatial distribution[J]. Journal of Sound and Vibration, 2016,367:114—128.
[8] 李增光,吴天行. 铁道车辆-轨道-高架桥耦合系统振动功率流分析[J]. 振动与冲击, 2010,29(11):78—82.
Li Zengguang,Wu Tianxing. Analysis of vibration power flow for a railway vehicle track viaduct coupled system[J].Journal of Vibration and Shock,2010,29(11):78—82.
[9] Wu T X, Liu J H. Sound emission comparisons between the box-section and U-section concrete viaducts for elevated railway[J]. Noise Control Engineering Journal, 2012, 60(4):450—457.
[10] Li Q, Li W Q, Wu D J, et al. A combined power flow and infinite element approach to the simulation of medium-frequency noise radiated from bridges and rails[J]. Journal of Sound and Vibration, 2016, 365:134—156.
[11] Wu T X, Thompson D J. The vibration behavior of railway track at high frequencies under multiple preloads and wheel interactions[J]. Journal of the Acoustical Society of America, 2000, 108(3): 1046—1053.
[12] Wu T X, Thompson D J. Theoretical investigation of wheel/rail non-linear interaction due to roughness excitation[J].Vehicle System Dynamics, 2000, 34(4): 261—282.
[13] Thompson D J. Railway Noise and Vibration: Mechanisms, Modeling and Means of Control[M]. UK: Elsevier Science Ltd., 2009.
[14] Li Q, Xu Y L, Wu D J,et al. Computer-aided nonlinear vehicle-bridge interaction analysis[J]. Journal of Vibration and Control,2010, 16(12):1791—1816.
[15] Song X D, Li Q, Wu D J. Investigation of rail noise and bridge noise using a combined 3D dynamic model and 2.5D acoustic model[J]. Applied Acoustics,2016,109:5—17.
[16] ISO3095:2005: railway applications-acoustics-measurement of noise emitted by rail bound vehicles[S]. Britain: British Standards Institution, 2006.
