声黑洞理论应用于板类结构的轻量化减振分析

贾秀娴， 杜 宇， 于 野， 赵坤民,2

(1.大连理工大学汽车工程学院, 辽宁 大连 116024;2.合肥工业大学工业与装备技术研究院, 安徽 合肥 230000)

1 概 述

由于能源紧缺和环境污染问题日趋严重，节能减排技术的研发变得尤为重要。在实现节能减排方面，轻量化有着立竿见影的效果[1-2]。车身的减重一般通过减薄壁板或者使用轻质替代材料的手段来实现，这种措施必然使车身壁板面密度降低，从而导致了车身结构动态性能弱化及隔声降噪性能下降[3-4]。为降低车辆振动和噪声水平，满足舒适性要求，通常要采取车身附加阻尼层、增加结构刚度等措施。但这些措施无疑又反过来增加了结构的重量，从而限制了轻量化程度的提高。因此，在实现结构轻量化的同时，如何进一步提高其振动噪声性能是目前需解决的问题。

一种基于声黑洞(Acoustic Black Hole，简称ABH)理论的新型结构可以潜在地实现使用较少附加质量有效控制结构振动噪声响应的目的。所谓声黑洞结构是指厚度符合某种幂指数关系分布且逐渐缩减到0的结构。当受到外界激励时，该结构具有将弯曲波束缚在尖锐边缘而不发生反射的特性[5]。

理论上，声黑洞结构可以吸收接近100%的入射波能量，然而任何实际结构都不可能达到厚度为零。加工过程中的制造偏差、切割工具引起的卷曲以及过早的切断，使得实际存在的ABH结构边缘均具有一个具体的厚度h0，如图1所示，其反射能量可达50%～70%[6]。但是，即使边缘厚度的存在、制造工艺不足够精准等缺陷会削弱ABH效应，事实证明声黑洞结构也能够广泛地应用，并起到减振降噪的作用[7]。为了弥补实际加工对ABH效应的削弱，在ABH结构末端附加少量的阻尼材料，可使整体结构在宽频带内达到有效的减振效果[8-10]。例如，当ABH理论应用于涡扇叶片的末端时结构的共振峰值显著降低，再附加适量的阻尼材料后涡扇的气流激振产生更大的衰减[11]。

图1 变厚度板模型Fig．1 Plate structure with varying thickness

图2 二维ABH结构的应用Fig．2 Application of two-dimensional ABH indentation

除了图1所述的楔形末端结构之外，Kroylov等将ABH结构在板厚仅沿长度或宽度单方向变化(一维)的应用推广到了沿两个方向同时变化(二维)的应用，图2所示为二维ABH在板结构中的几种应用方式，这一拓展使ABH效应得到更加高效、广泛地应用[12-13]。附加阻尼层也在很大程度上弥补了实际制造过程对二维ABH结构造成的削弱，使反射系数大大降低[14]。当带孔式ABH应用于结构中时，由于孔的边缘是尖锐的断面，可以增大能量衰减效率，同时孔的直径越大减振效果越好[15]。在较高频率的激励条件下，带孔的ABH结构(无阻尼材料附加)比无孔ABH结构(附加阻尼层)减振降噪效果更好。一般来说，孔的直径越大、变厚度区域的直径越大、ABH结构的个数越多减振的效果越好[16]。

以上内容简述了声黑洞理论的应用发展，在实际应用中，与理想的声黑洞结构相比会产生一定量的反射能量。针对这一缺陷，大部分的研究学者均采取了附加阻尼层的措施来提高减振效果。阻尼层在高频范围内具有高效的宽带减振功能，但是在中低频范围内的减振效率就会很低。然而，动力吸振器(Dynamic Vibration Absorber，简称DVA)作为另一种普遍的减振措施，是一种调谐的弹簧质量系统，可以有效的应用于中、低、高频[17]，缺点就是减振控制的频带相对较窄。

因此，本文提出了将声学黑洞的声聚焦效应与动力减振器相结合的概念，并针对中低频范围内的振动特性，通过有限元分析研究了对声黑洞结构附加DVA后在减重及振动噪声控制方面的可行性，同时对声黑洞结构附加阻尼层后进行分析，对比两种方式在减重及振动噪声控制方面的表现。

2 声黑洞的基本理论

忽略转动惯量和剪切变形的影响，薄板中弯曲波的波速cb为[18]

(1)

式中f为频率，h为板的厚度，E为杨氏模量，ρ为板材料的密度，υ为泊松比。若板的厚度按下式所示的幂次定律变化

hx=εxm

(2)

那么变厚度区域内随坐标x变化的弯曲波的波速cb(x)可以表示为

(3)

公式(2),(3)中，x为沿板长度(或宽度)方向的坐标，ε和C为常数，m为正有理数，ω为角频率。

薄板结构中，波数的表达式为

(4)

(5)

将式(4)带入式(5)中可得

(6)

根据式(6)可知，在变厚度区域内，归一化波数NWV是关于频率ω以及位置x的函数。当频率很小、x值较大的情况下变厚度区域的平滑性较容易破坏。同时，这一约束条件也包含了对波的频率以及比例参数ε的限制

(7)

若使ABH结构对弯曲波起到聚焦的作用，波长λ至少要小于ABH的特征尺寸x1，即kx1≥1。令kx1=1，可得ABH聚焦效应的起始频率

(8)

根据式(8)计算，本文中所采用的ABH模型起到聚焦效应的起始频率为333.3 Hz。由于本文中的声黑洞模型并非理想的声黑洞模型，即其最薄厚度没有达到零，因此结构中会产生反射能量，其聚焦效应也无法达到理想的效果，本文没有对起始频率前后进行着重的对比分析。

3 有限元分析

3.1 有限元模型

本文在Hypermesh中建立了5个有限元模型，并使用Nastran进行计算分析：(1)均匀厚度板(简称UTP)，(2)附加阻尼层的均匀厚度板(简称UTP-Damp)，(3)嵌入2个ABH特征的变厚度板(简称VTP-ABH)，(4)附加阻尼块的变厚度板(简称VTP-ABH-Damp)，(5)附加DVA的变厚度板(简称VTP-ABH-DVA)。

图3 嵌入2个ABH结构的矩形板模型Fig．3 Plate model embedded with two circular indentations of ABH

板的尺寸和参数如图3及表1所示，ABH区域厚度的变化遵循h(x) =εxm+h0，激励力施加在板的几何中心，记为点I，振动响应检测点位于板的垂直中心线上，距离下方的边30 mm，记为点O。板结构的边界条件为2个短边简支、另外2条边自由。表格中ρ为材料的密度，E为杨氏模量，υ为泊松比，η为材料的损失因子，h为厚度，m和k分别为质量和刚度。下角标“d” 代表阻尼，“D” 代表DVA。上角标“U”代表均匀厚度板，“V” 代表变厚度板。

表1 仿真模型的结构参数和材料参数

图4 模型结构图Fig．4 Schematics of the plate structures

在UTP-Damp模型中，将一薄层阻尼层附加在均匀厚度板上，厚度为0.49mm；ABH特征上附加阻尼块及DVA的实施方式如图4所示；不同板结构上所附加阻尼、DVA的质量相同。有限元网格模型如图5所示，浅灰色所示为阻尼，深灰色所示为板结构。均匀厚度板的网格划分使用壳单元，阻尼层与板结构之间为刚度连接，如图5(a)所示。变厚度板结构使用四面体单元进行划分，阻尼块与VTP-ABH结构之间的连接为共享节点，保证两者之间具有相同的自由度。

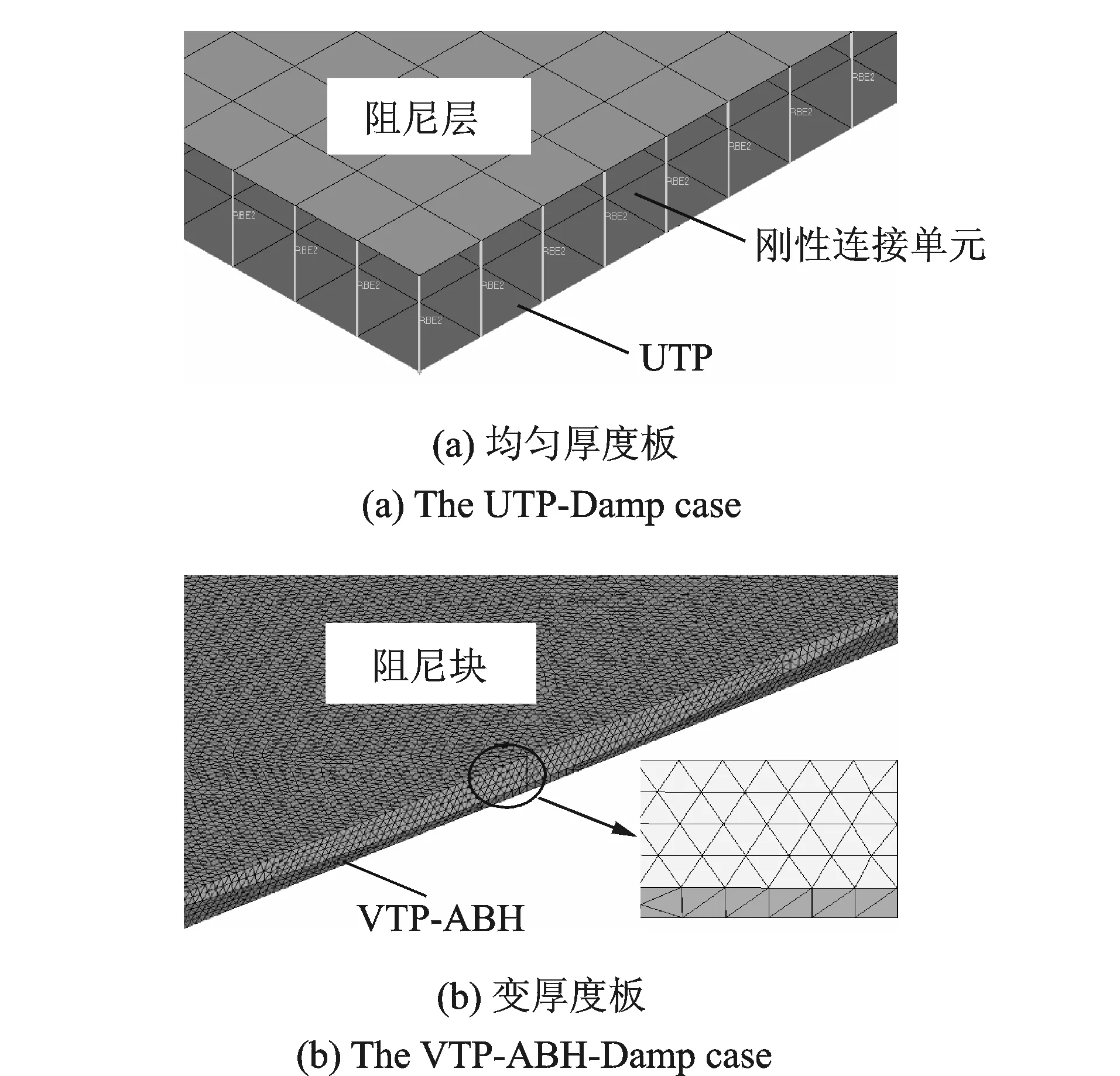
图5 附加阻尼的有限元网格模型Fig．5 Grid details of FE models

3.2 模型验证

为了验证仿真模型及结果的准确性，本文设计了与仿真中设置相同的实验，并经过铣削加工得到包含两个变厚度区域的VTP-ABH模型，对其在0～3200Hz激励频率范围进行了频率响应分析，实验装置如图6所示。

图6 实验装置Fig．6 Experimental setup

实验与仿真的对比结果如图7所示，在整个频率带内，2条频响曲线差别较小，造成这种差距的原因可能是由于VTP-ABH模型在铣削加工过程中产生的几何误差。最后2阶共振峰处的固有频率差别较大，原因可能是由于实验过程中边界条件的实施没能够完美地达到简支的条件。总体来讲，仿真与实验的整体响应趋势合理地匹配，可验证仿真模型的可行性。

图7 加速度传递率的结果对比(实线：仿真模型;虚线：实验模型)Fig．7 Acceleration transmissibility for the VTP-ABH case (solid line: simulation; dash line: experimental)

4 减振控制分析

4.1 声黑洞结构的聚焦特性

通过有限元分析得到在某一激励频率下等厚度板(UTP)与变厚度板(VTP-ABH)的加速度响应云图。如图8(b)所示变厚度板的变厚度区域中央的响应达到最大且外部区域的振动响应相对较小，而等厚度板加速度响应云图中较大的振动响应分布在多个区域(图8(a))，图8(b)所示的聚焦现象就是声黑洞结构的聚焦效应。

图8 2800 Hz激励频率下的加速度响应云图Fig．8 Contour of acceleration responses of plate structures at 2800 Hz

4.2 基于声黑洞理论，附加阻尼块、DVA的减振措施分析

分别对VTP-ABH结构附加阻尼块和DVA，进行进一步的减振控制，模型如3.1节所述，计算各板结构的平均加速度响应值As，即在激励频率范围0～3200 Hz内板结构上所有节点振幅的平均值，计算公式为

(9)

式中ai为第i个节点的加速度值，i=1,2,3,…,n;n为仿真模型中的总节点个数。

图9 附加阻尼对结构的平均加速度响应分析Fig．9 Averaged acceleration response

由图9 (a)可知附加阻尼层之后的UTP-Damp在整个频率范围内平均降低了1.3～2.0 dB。而将等量的阻尼块填充于VTP-ABH的变厚度区域之后，结构的平均加速度响应值在第1,6,7个峰值处均降低了约10 dB，且在第2至第5个峰值也有5 dB左右的衰减，结果如图9 (b)所示。对比UTP-Damp和VTP-ABH-Damp，由图9 (c)观察到，后者的平均加速度响应值在第1，3，4，5，7个峰值降低约5 dB，在第6个峰值降低了9.4 dB。同时，由表2所示，通过质量的对比可知，VTP-ABH-Damp要比UTP-Damp轻11.8%。综上，声黑洞结构的嵌入不仅使等量的阻尼材料在减振降噪方面起到显著的振动衰减作用，同时也为轻量化做了较大贡献。

表2 各模型的总质量(单位：kg)

本文中DVA的参数针对VTP-ABH模型的第1,3个共振频率而设计，参数如表1所示。对变厚度板附加阻尼块和DVA之后减振效果的对比如图10所示。与VTP-ABH相比，VTP-ABH-DVA的振动响应在第1,3个共振峰处分别降低了17.4 dB和17.2 dB，比VTP-ABH-Damp的平均加速度响应值低8.4,10.7 dB，附加DVA之后的优势显而易见。如果在板结构上增加ABH单元的个数，DVA的个数也可根据需求而增加，那么理论上就可以使得更多共振频率下的振动响应得到较大限度的衰减，分布式DVA的多共振峰减振优势可待研究。

图10 变厚度板附加阻尼块和DVA之后结构的平均加速度响应对比Fig．10 Averaged acceleration response comparison among VTP-ABH, VTP-ABH-Damp and VTP-ABH-DVA

5 结 论

弯曲波的速度随着板厚度的减少而降低，因此在理想情况下，当板的截面厚度平滑地减少为零时，弯曲波不会发生反射。然而，由于实际条件的限制，板的厚度不可能平滑地减小到零，那么控制弯曲波随着板的厚度而变化就成为了声黑洞理论的基础思想。声黑洞理论所产生的声聚焦效应优势是可以把振动能量主动地“汇集”到某一特定区域，然后在这一区域“有的放矢”地采取控制措施，从而达到使用较少的附加质量来降低结构振动响应的目的。

本文采用有限元仿真分析的方法对基于ABH理论的变厚度板的聚焦效果进行了验证，同时对比分析了附加阻尼块和DVA对其进行减振降噪的效果。结果表明，经过变厚度板的聚焦效应，再对聚焦区域采取局部减振处理的方法，无论是对结构进行减振降噪还是实现轻量化都是非常有效的，特别是附加DVA的方式针对低频率下的减振效果更加明显。未来的工作将对分布式DVA应用于多个ABH结构排列的变厚度板进行进一步的研究。

[1] Ashley S. Shedding pounds on a magnesium diet[J]. Automotive Engineering International, 2010, 118(3).

[2] Edited by Center for Automotive Research. Automotive technology: Greener products[R]. Changing Skills-Lightweight Materials & Forming Report, 2011.

[3] Kinsler L E, Frey A R, Adams C E. Fundamentals of Acoustics[M]. 4th ed. John Wiley, 2000.

[4] 陈馨蕊, 郝志勇, 刘 迟. 汽车镁质复合仪表板传声损失的实验及仿真研究[J]. 振动与冲击, 2010, 29(011): 38—40.

Chen X R, Hao Z Y, Liu C. Test and simulation of sound transmission loss for a magnesium alloy laminated automotive dash[J]. Journal of Vibration & Shock, 2010,29(011):38—40.

[5] Krylov V V, Tilman F. Acoustic ‘black holes’ for flexural waves as effective vibration dampers[J]. Journal of Sound and Vibration, 2004, 274(3): 605—619.

[6] Mironov M A. Propagation of a flexural wave in a plate whose thickness decreases smoothly to zero in a finite interval[J]. Soviet Physics-Acoustics, 1988, 34: 318—319.

[7] Bowyer E P, O’Boy D J, Krylov V V, et al. Effect of geometrical and material imperfections on damping flexural vibrations in plates with attached wedges of power law profile[J]. Applied Acoustics, 2012, 73(5):514—523.

[8] Krylov V V, Winward E. Experimental evidence of the acoustic black hole effect for flexural waves in tapered plates[C]. International Congress on Sound and Vibration, 2005:43—49.

[9] Krylov V V. Damping of resonant vibrations utilising the acoustic black hole effect[C]. International Conference Novem., OAI, 2005:1—12.

[10] O’Boy D J, Krylov V V, Kralovic V. Damping of flexural vibrations in rectangular plates using the acoustic black hole effect[J]. Journal of Sound & Vibration, 2010, 329(22):4672—4688.

[11] Bowyer E P, Krylov V V. Damping of flexural vibrations in turbofan blades using the acoustic black hole effect[J]. Applied Acoustics, 2014, 76(1):359—365.

[12] Krylov V V. Propagation of plate bending waves in the vicinity of one- and two-dimensional acoustic ‘black holes’[C]. ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, OAI, 2007.

[13] Krylov V V, Winward R E T B. Experimental investigation of the acoustic black hole effect for flexural waves in tapered plates[J]. Journal of Sound & Vibration, 2007, 300(1-2):43—49.

[14] Kralovic V, Bowyer E P, Krylov V V, et al. Experimental study on damping of flexural waves in rectangular plates by means of one-dimensional acoustic ‘black holes’[C]. 14th International Acoustic Conference, 2009,92(2):S1.

[15] Bowyer E P, O’Boy, D J, Kralovic V V, et al. Experimental investigation of damping flexural vibrations using two-dimensional acoustic ‘black holes’[C]. Proceedings of the International Conference on Noise and vibrotion Engineering(ISMA 2010),Leuven,Belgiam, 2010.

[16] Bowyer E P, O’Boy D J, Krylov V V, et al. Experimental investigation of damping flexural vibrations in plates containing tapered indentations of power-law profile[J]. Applied Acoustics, 2013, 74(4):553—560.

[17] 朱桂东, 郑钢铁, 邵成勋. 基于行波模型的航天器附件动力吸振分析[J]. 振动工程学报, 1998,11(2):138—143.

Zhu G, Zheng G. Analysis of dynamic vibration absorber for spacecraft with flexible appendages via travelling wave approach[J]. Journal of Vibration Engineering, 1998,11(2):138—143.

[18] Conlon S C, Semperlotti F, Fahniline J B. Passive control of vibration and sound transmission for vehicle structures via embedded acoustic black holes[C]. Proceedings of Noise-Con 2013, Denver, Colorado, August 26-28, 2013.

[19] Krylov V V. Localised acoustic modes of a quadratically-shaped solid wedge[J]. Moscow University Physics Bulletin, 1990, 45(6): 65—69.

[20] Krylov V V, Shuvalov A L. Propagation of localised flexural vibrations along plate edges described by a power law[J]. Proceedings of the Institute of acoustics, 2000, 22:263—270.

[21] Feurtado P A, Conlon S C, Semperlotti F. A normalized wave number variation parameter for acoustic black hole design[J]. Journal of the Acoustical Society of America, 2014, 136(2):148—152.

[22] Conlon S C, Fahnline J B, Semperlotti F. Numerical analysis of the vibroacoustic properties of plates with embedded grids of acoustic black holes[J]. Journal of the Acoustical Society of America, 2015, 137(1):447—457.